Министерство образования и науки Российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ростовский государственный строительный университет»

Утверждено

на заседании кафедры физики 08 февраля 2012 г.

Зав. кафедрой физики

__________________/Н.Н. Харабаев/

Учебно-методическое пособие

КОНСПЕКТ ЛЕКЦИЙ по физике

(для всех специальностей)

Ростов-на-Дону

2012

УДК 531.383

Учебно-методическое пособие. Конспект лекций по физике (для всех специальностей). – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 103 с.

Содержится конспект лекций по физике, основанный на учебном пособии Т.И. Трофимовой «Курс физики» (изд-во Высшая школа).

Состоит из четырех частей:

I. Механика.

II. Молекулярная физика и термодинамика.

III. Электричество и магнетизм.

IV. Волновая и квантовая оптика.

Предназначено для преподавателей и студентов в качестве теоретического сопровождения лекций, практических и лабораторных занятий с целью достижения более глубокого усвоения основных понятий и законов физики.

Рекомендуется для самостоятельной работы студентов всех специальностей очной и заочной формы обучения.

УДК 531.383

Составители: проф. Н.Н.Харабаев

доц. Е.В.Чебанова

проф. А.Н. Павлов

Редактор Н.Е.Гладких

Темплан 2012 г., поз. Подписано в печать

Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 4,0.

Тираж 100 экз. Заказ

_________________________________________________________

Редакционно-издательский центр

Ростовского государственного строительного университета

334022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2012

Часть I. Механика

Тема 1. Кинематика поступательного и вращательного движения. Кинематика поступательного движения

Положение материальной точки Ав декартовой системе координат в данный момент времени определяется тремя координатамиx,y и zилирадиусом-вектором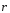– вектором, проведенным из начала системы координат в данную точку (рис. 1).

Движение материальной точки определяется в скалярном виде кинематическими уравнениями: x = x(t),у = y(t),z = z(t),

или в векторном виде уравнением: .

Траектория движения материальной точки – линия, описываемая этой точкой при её движении в пространстве. В зависимости от формы траектории движение может быть прямолинейным или криволинейным.

Материальная точка, двигаясь по произвольной траектории, за малый промежуток времени Dtпереместиться из положенияАв положениеВ, пройдя при этом путьDs, равный длине участка траекторииАВ (рис. 2).

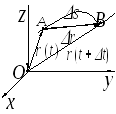
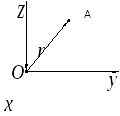
Рис. 1 Рис. 2

Вектор 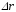, проведенный из начального положения движущейся точки в момент времениt в конечное положение точки в момент времени (t+Dt), называется перемещением, то есть .

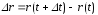Вектором средней скорости 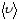называется отношение перемещения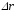к промежутку времениDt , за который это перемещение произошло:

.

Направление вектора средней скорости 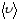совпадает с направлением вектора перемещения.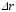

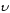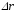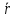Мгновенной скоростью (скоростью движения в момент времени t) называется предел отношения перемещения к промежутку времениDt, за который это перемещение произошло, при стремлении Dt к нулю: = ℓim_Δt→0Δ/Δt = d/dt =

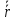
Вектор мгновенной скорости 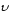направлен по касательной, проведенной в данной точке к траектории в сторону движения. При стремлении промежутка времениDt к нулю модуль вектора перемещения стремится к величине путиDs, поэтому модуль вектора v может быть определен через путь Ds: v = ℓim_Δt→0Δs/Δt = ds/dt =

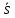
Если скорость движения точки со временем изменяется, то быстрота изменения скорости движения точки характеризуется ускорением.

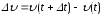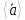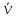Средним ускорением ‹a› в интервале времени от t до (t + Dt) называется векторная величина, равная отношению изменения скорости () к промежутку времениDt, за который это изменение произошло: =Δ/Δt

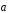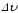Мгновенным ускорением илиускорением движения точки в момент времени t называется предел отношения изменения скорости к промежутку времениDt, за который это изменение произошло, при стремлении Dt к нулю:

,

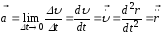где 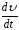– первая производная от функции 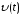по времени t,

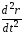–вторая производная от функции по времени t.

Эти производные принято обозначать соответственно в виде: 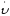и.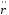

Вектор ускорения 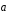может быть разложен на две составляющие: тангенциальную 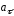и нормальную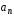, то есть:

.

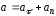Тангенциальная составляющая 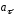определяет быстроту изменения модуля скорости : .

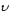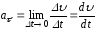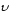Вектор направлен по касательной к траектории движения и для ускоренного движения совпадает с направлением вектора скорости, а для замедленного движения – противоположен вектору скорости.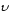

Нормальная составляюща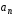я определяет быстроту изменения направления скорости v: a_n = v²/r , где r – радиус кривизны траектории движения.

Вектор 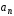направлен по нормали к траектории движения к центру ее кривизны (поэтому нормальную составляющую ускорения называют также центростремительным ускорением).