33

Министерство образования и науки Российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ростовский государственный строительный университет»

Утверждено

на заседании кафедры физики

08 февраля 2012 г.

физика на заочном факультете

КРАТКИЙ КУРС ЛЕКЦИЙ

ЧАСТЬ II. ЭЛЕКТРИЧЕСТВО и МАГНЕТИЗМ.

ВОЛНОВАЯ И КВАНТОВАЯ ОПТИКА

Учебно-методическое пособие для бакалавриата

всех профилей по направлению подготовки

270800 «Строительство»

Ростов-на-Дону

2012

УДК 531.383

Учебно-методическое пособие для бакалавриата всех профилей по направлению подготовки 270800 «Строительство».

Физика на заочном факультете. Краткий курс лекций. Часть II. Электричество и магнетизм. Волновая и квантовая оптика. – Ростов н/Д: Рост. гос. строит. ун-т, 2012. – 35 с.

Содержится краткий курс лекций по физике, основанный на учебном пособии Т.И. Трофимовой «Курс физики» (изд-во Высшая школа), соответствующем действующей программе курса физики для бакалавриата всех профилей по направлению подготовки 270800 «Строительство».Краткий курс лекций по физике состоит из двух частей:

Часть I. Механика. Молекулярная физика и термодинамика.

Часть II. Электричество и магнетизм. Волновая и квантовая оптика.

Часть I завершается списком вопросов к зачету.

Часть II завершается списком вопросов к экзамену.

Предназначено для использования преподавателями и студентами в качестве теоретического сопровождения лекций, практических занятий и лабораторного практикума с целью достижения более глубокого усвоения основных понятий и законов физики.

Рекомендуется для студентов бакалавриата заочного факультета РГСУ по всем профилям направления подготовки 270800 «Строительство».

УДК 531.383

Составители: проф. Н.Н.Харабаев

доц. Е.В.Чебанова

проф. А.Н. Павлов

доц. Н.В. Кривошеев

Редактор Н.Е.Гладких

Темплан 2012 г., поз. 74

Подписано в печать 9.11.11

Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 1,0.

Тираж 100 экз. Заказ

___________________________________________________________

Редакционно-издательский центр

Ростовского государственного строительного университета

334022, Ростов-на-Дону, ул. Социалистическая, 162

© Ростовский государственный

строительный университет, 2012

Электростатика Тема 1. Теорема Остроградского-Гаусса для электростатического поля Электростатическое поле – это особый вид материи, с помощью которой происходит взаимодействие заряженных тел.

Закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами q₁ и q₂ прямопропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстояния r между ними:

, где (₀ – электрическая постоянная);

 – диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия зарядов в данной среде меньше, чем в вакууме.

Элект­рические поля, которые создаются неподвижными электрическими зарядами, называ­ются электростатическими.

Напряженность электростатического поля в данной точке есть физическая величина , определяемая силой, действующей на пробный точечный положительный заряд q₀ , помещенный в эту точку поля, то есть:

.

Электростатическое поле может быть изображено графически с помощью силовых линий. Силовая линия — это такая линия, касательная в каждой точке к которой совпадает по направлению с вектором напряженности электростатическго поля в данной точке (рис. 1, 2).

Е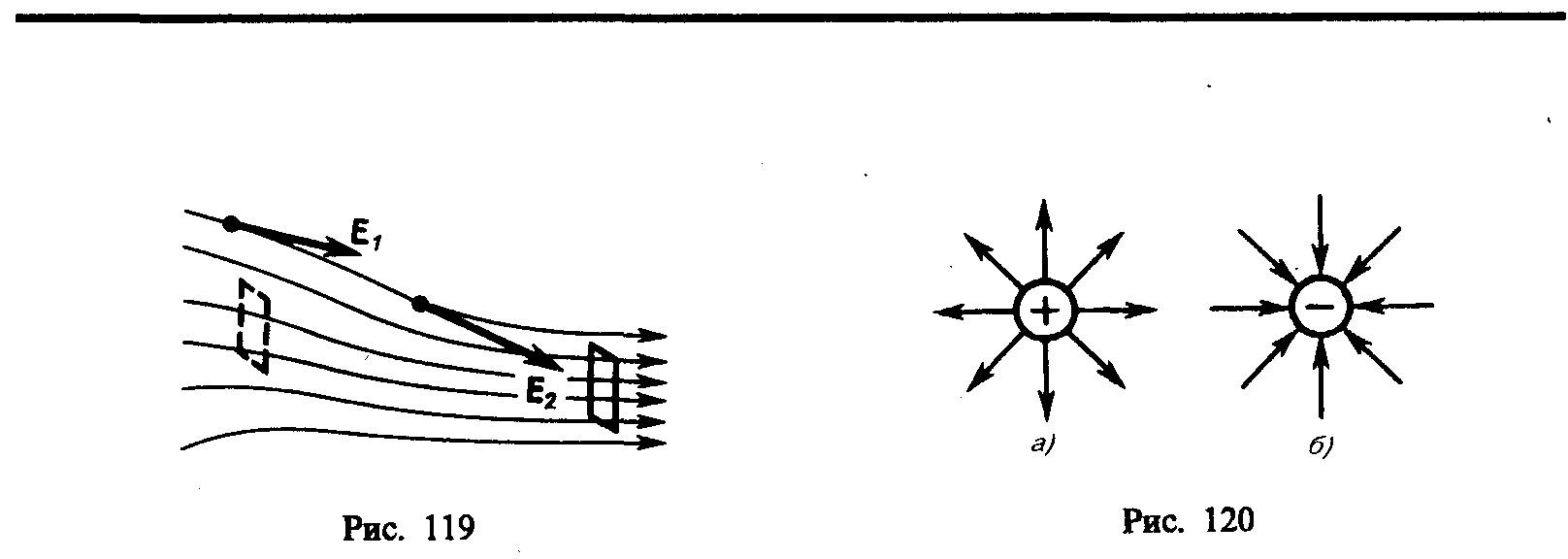сли поле создается точечным зарядом, то силовые линии – это радиальные прямые, выходящие из положительного заряда (рис. 2,а), и входя­щие в отрицательный заряд (рис. 2, б).

Рис. 1 Рис. 2

С помощью силовых линий можно характеризовать не только направление, но и величину напряженности электростатического поля, связывая ей с густотой силовых линий. Большей густоте силовых линий соответствует большая величина напряженности (рис. 1, 2). Количественно числу силовых линий, прони­зывающих единичную площадку, расположенную перпендикулярно силовым линиям, ставится в соответствие величина напряженности электростатического поля. В этом случае определенному заряду q, создающему поле, соответствует определенное число N силовых линий, выходящих (для ) из заряда или входящих (для ) в заряд, а именно: .

Поток вектора напряженности электростатического поля через произвольную площадкуS характкризуется числом силовых линий, пронизывающих данную площадку S.

Если площадка S перпендикулярна силовым линиям (рис. 3), то поток Ф_Е вектора напряженности через данную площадкуS : .

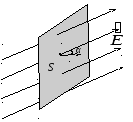
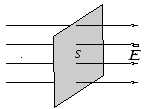
Рис. 3 Рис. 4

Е

Рис. 3

сли же площадка S расположена неперпендикулярно силовым линиям электро-статического поля (рис. 4), то поток вектора через данную площадкуS :

,

где α – угол между векторами напряженности и нормалик площадкеS.

Д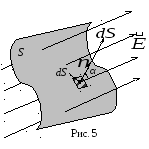ля того, чтобы найти потокФ_Е вектора напряженности через произвольную поверхностьS, необходимо разбить эту поверхность на элементарные площадки dS (рис. 5), определить элементарный поток dФ_Е через каждую площадку dS по формуле:

,

а затем все эти элементарные потоки dФ_Е сложить, что приводит к интегрированию:

,

где α – угол между векторами напряженности и нормалик данной элементарной площадкеdS .

Е

сли ввести вектор(рис. 5) как вектор, равный по величине площади площадкиdS и направленный по вектору нормали к площадкеdS , то величина , где – угол между векторами иможет быть записана в виде скалярного произведения векторови, то есть, как, а полученное соотношение для потока векторапримет вид:

.

Теорема Остроградского - Гаусса для электростатического поля.

Теорема Остроградского - Гаусса для электростатического поля связывает между собой величину потока Ф_Е вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность S с величиной заряда q, заключенного внутри данной замкнутой поверхности S (рис. 6).

П

Рис. 6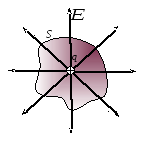

оскольку все силовые линии, выходящие из заряда (для) или входящие в заряд (для ), пронизывают произвольную замкнутую поверхность S, охватывающую этот заряд (рис. 6), то величина потока Ф_Е вектора через эту поверхностьS будет определяться числом N силовых линий выходящих из заряда (для ) или входящих в заряд (для ):

.

Это соотношение есть теорема Остроградского-Гаусса для электростатического поля.

Так как поток считается положитель­ным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, то в случае, если внутри произвольной замкнутой поверхности S находится не один, а несколько (n) разноименных зарялов, то теорема Остроградского - Гаусса для электростатического поля формулируется следующим образом:

поток вектора напряженности электростатического поля в вакууме через произ­вольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ₀ :

.