Формула Ціолковського.

Важливий вклад в механіку тіл змінної маси стосовно до конкретних завдань реактивної техніки вніс російський вчений К.Е. Ціолковський (1903 р. ”Исследование мировых пространств реактивными приборами”), в якому теоретично доведена і обгрунтована можливість практичного використання реактивного руху для освоєння космосу.

Основна ідея цих досліджень – ідея про використання багатоступінчастих ракет для космічних польотів.

Розглянемо найпростіший реактивний рух ракети – прямолінійний горизонтальний рух без дії сили опору повітря (у безповітряному просторі) (рис. 3.6).

Рис. 3.6.

Використаємо рівняння Мещерського в проекціях на вибрану систему координат

,

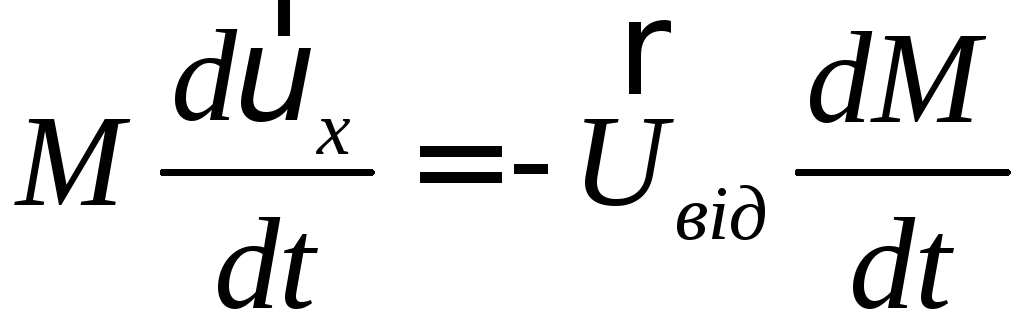де М = М(t).

Відокремлюємо змінні:

у скалярній формі

.

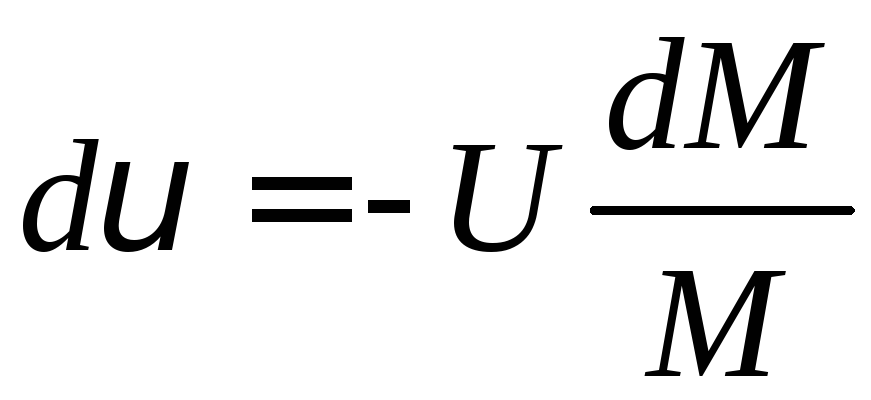Швидкість виходу газів із ракети протилежні за напрямом швидкості ракети.

Інтегруючи ліву і праву частини, одержимо:

,

де – початкова маса ракети;М – маса ракети після згорання палива.

(для )(3-17)

Остання формула носить назву формули Ціолковського.

Кінцева швидкість, яку досягає ракета при відсутності дії зовнішніх сил, прямо пропорційна відносній швидкості відділення частинок відносно стартової маси ракети в даний момент часу.

В момент повного згорання палива:

і тоді

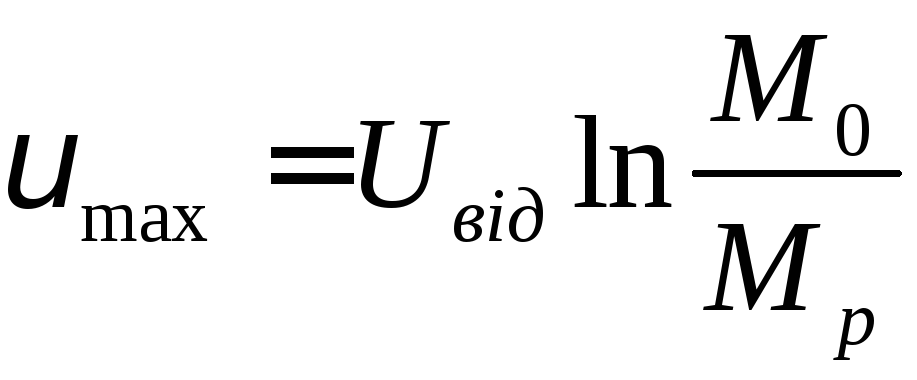
Відношення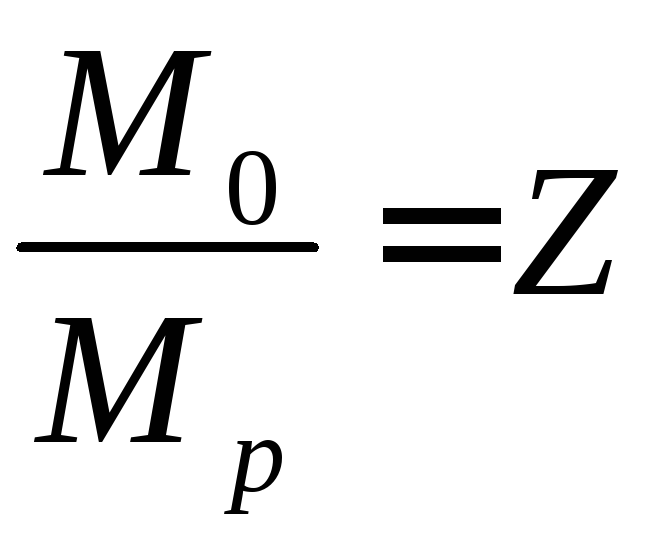– число Ціолковського.

Обчислимо максимально можливу швидкість однієї ступені ракети

а) км/с – визначається максимально допустимою температурою згорання палива;

б) – визначається міцністю конструкції матеріалу ракети. Конструкція не може мати масу меншу 10% загальної маси

Тоді: км/с.

Точніше в ідеальному випадку не можливо досягти I космічної швидкості: км/с.

Звідси ідея: використання багатоступінчатих ракет. Тоді закон руху ракети запишемо як:

; .

Практичне заняття 3.1 Тема: Закон збереження імпульсу для замкненої механічної системи. Основні формули

Імпульс (кількість руху) матеріальної точки є векторна величина

(1)

Імпульс системи матеріальних точок рівний (за визначенням) векторній сумі імпульсів всіх частинок, які утворюють систему:

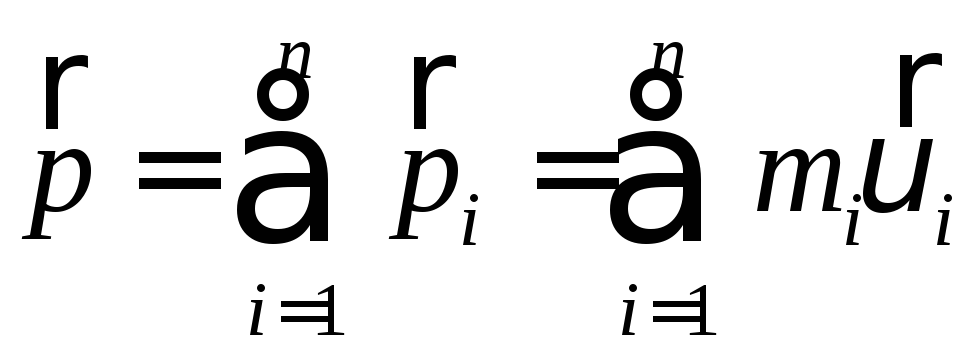(2)

Центром інерції системи матеріальних точок називається точка С, положення якої в просторі визначається радіусом-вектором, початок якого знаходиться у довільній точці О і рівним

, (3)

де – масаі-ї матеріальної точки, – її радіус-вектор з початком в тій же точціО, М – маса всієї системи.

Імпульс системи матеріальних точок рівний добутку маси М системи на швидкість руху її центру інерції:

(4)

Систему тіл, які взаємодіють називають замкнутою, якщо на неї ззовні не діють інші тіла. Для такої системи виконується закон збереження імпульсу: імпульс замкнутої системи є величина постійна, тобто

(5)

В координатній формі:

(5а)

Методичні вказівки

Перевага закону збереження імпульсу для вирішення задач динаміки полягає в тому, що він, зв’язуючи початкове і кінцеве значення імпульсу замкнутої системи, дозволяє виключати з розгляду внутрішні сили, тобто сили взаємодії частин системи. Тому закон застосовують в тих задачах, в яких сили взаємодії між окремими тілами системи є величинами змінними, причому характер їх зміни в часі складний або взагалі невідомий (наприклад, сили, що виникають при ударі).

Рівняння (5), що виражає закон збереження імпульсу, є векторним. Тому, знаходячи вектор , треба керуватися правилом складання векторів або, вибравши осі проекційОх і Оу, записати закон збереження імпульсу в скалярній формі двома рівняннями:

Якщо імпульси всіх тіл системи направлені уздовж однієї прямої, то, вибравши цю пряму за вісь проекцій, відразу записують закон збереження імпульсу в скалярній формі:

,

де– сума проекцій імпульсів всіх тіл системи.

Закон збереження імпульсу справедливий для замкнутих систем. Проте його можна застосовувати і для систем, на які діють зовнішні сили за умови, що їх сума рівна нулю: .

Якщо ж 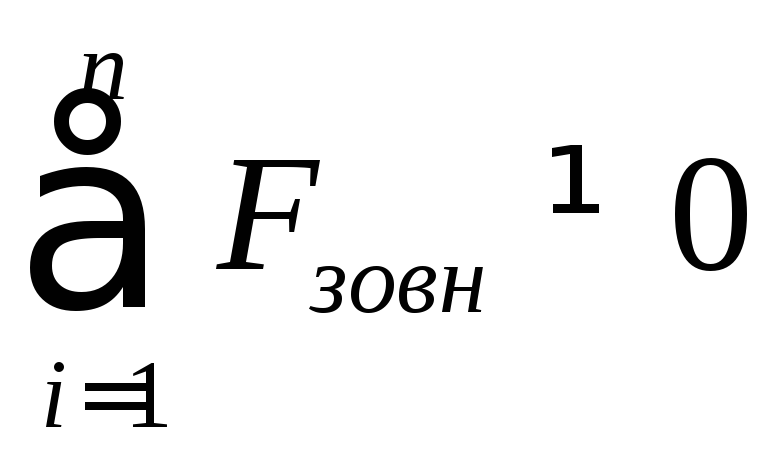, але виявиться, що сума проекцій всіх зовнішніх сил на деяку вісь (Ох) рівна нулю, то

,

тобто проекція імпульсу системи на напрям, в якому зовнішні сили не діють (або врівноважуються), є величина постійна.

Приклад 1. На рейках, на горизонтальній площині стоїть платформа з піском загальною масою М = 5·10³ кг. У платформу потрапляє снаряд масою = 5 кг, що летить зі швидкістю= 400 м/с. Снаряд летить уздовж рейок під кутом= 36^о до горизонту (рис. 1). Знайти швидкість платформи, якщо снаряд застряє у піску.

Розв’язання.

Рис. 1.

Ця задача не може бути вирішена безпосередньо за допомогою законів Ньютона. Платформа набуває швидкості і в результаті взаємодії зі снарядом, але закон зміни сили цієї взаємодії в часі невідомий. Тому треба з’ясувати, чи можна вирішити цю задачу за допомогою законів збереження.

На систему платформа – снаряд, окрім сили взаємодії – сили, внутрішньої для цієї системи, діють сила тяжіння, сила нормальної реакції і сила тертя. В даному випадку унаслідок негоризонтального напряму швидкості снаряда сила нормальної реакції, що діє на платформу, під час взаємодії платформи і снаряда змінюватиметься. Отже, закон збереження імпульсу до даної системи не мажна застосувати.

Але якщо нехтувати силою тертя (в порівнянні з силою взаємодії платформи і снаряда), сума проекцій зовнішніх сил на горизонтальний напрям буде рівна нулю. Це означає, що проекція вектора повного імпульсу системи на горизонтальний напрям залишається постійною:

,

де – проекція імпульсу системи до взаємодії,– після взаємодії.

До взаємодії вектор-імпульс системи

або в скалярній формі

Після взаємодії

Звідси отримуємо

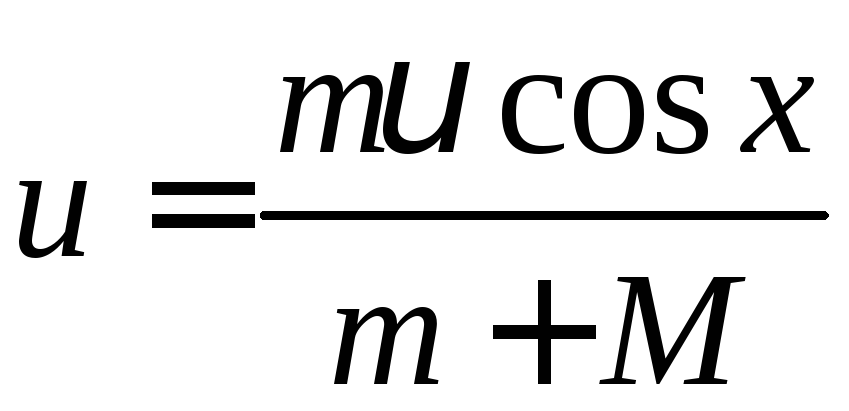= 0,32 м/с.

Приклад 2. Акробат масою М = 50 кг, маючи при собі груз = 5 кг, стрибає під кутом= 60^о до горизонту зі швидкістю = 6 м/с (рис. 2). У найвищій точці своєї траєкторії він кидає вантаж горизонтально назад з відносною швидкістю= 2 м/с. На скільки збільшиться дальність стрибка акробата внаслідок цього?

Розв’язання.

Рис. 2.

Збільшення дальності стрибка на величину обумовлене збільшенням горизонтальної швидкості гімнаста, що відбувається, внаслідок кидка вантажу.

У весь час руху на систему акробат – вантаж діє зовнішня сила – сила тяжіння. Але у верхній точці траєкторії, тобто у момент кидка, швидкості акробата і вантажа строго горизонтальні, проекція сили тяжіння на горизонтальний напрям рівна нулю.

Отже, імпульс системи до і після кидка буде постійним, при цьому слід припустити, що час кидка нескінченно малий.

Задачу зручно вирішувати в системі координат, яка рухається із швидкістю , де– горизонтальна складова швидкості акробата до кидка.

У системі координат, зв’язаній із Землею,

, (1)

де – горизонтально направлена швидкість акробата після кидка,– час руху акробата від верхньої точки траекторії до землі, який знаходиться за законом незалежності руху:

,

а максимальна висота підйому

,

звідки знаходимо

(2)

Для обчислення застосовуємо закон збереження імпульсу в системіх', у', яка рухається із швидкістю .

У цій системі координат імпульс системи акробат – вантаж до кидка , після кидка –, деМ – маса акробата. Отже

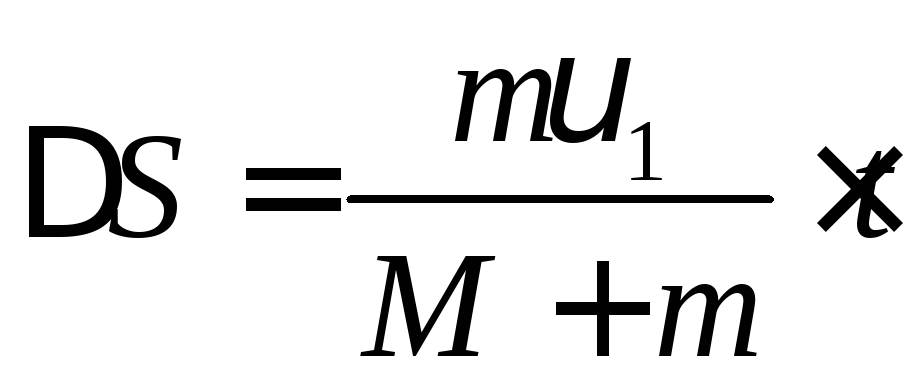(3)

Підставивши формули (2) і (3) в рівняння (1), отримаємо

= 0,095 м.

Приклад 3. Снаряд, що летів горизонтально зі швидкістю = 100 м/с, розривається на дві рівні частини на висотіН = 40 м. Одна частина падає через t = 1 сек на землю точно під місцем вибуху. Визначити величину і напрям швидкості другої частини снаряда відразу після вибуху.

Розв’язання.

Рис. 3.

Сили, що виникають при вибусі снаряда, настільки великі, що систему снаряд — дві його частини можна вважати замкнутою. Отже, повний вектор імпульсу системи за час вибуху не змінюється:

(1)

До вибуху вектор направлений горизонтально. Після вибуху повний вектор імпульсурівний сумі векторів імпульсів двох частин снаряда, на які він розривається. Один з цих векторів, згідно умові задачі, направлений строго по вертикалі, напрям і величину іншого вектора треба визначити. Рівність (1) можна переписати в скалярній формі, якщо ввести координатні осі: вісьх – по горизонталі, вісь у – вертикально вгору або вниз. Можна провести рішення і безпосередньо з векторної рівності (1). З рис. 3 видно, що

(2)

, (3)

де m – маса кожної частини снаряда; – його швидкість;– початкова вертикальна швидкість 1-ї частини снаряда;– початкова швидкість 2-ої частини.

Як видно з рис. 3

звідки

На основі закону падіння для 1-ої частини снаряда:

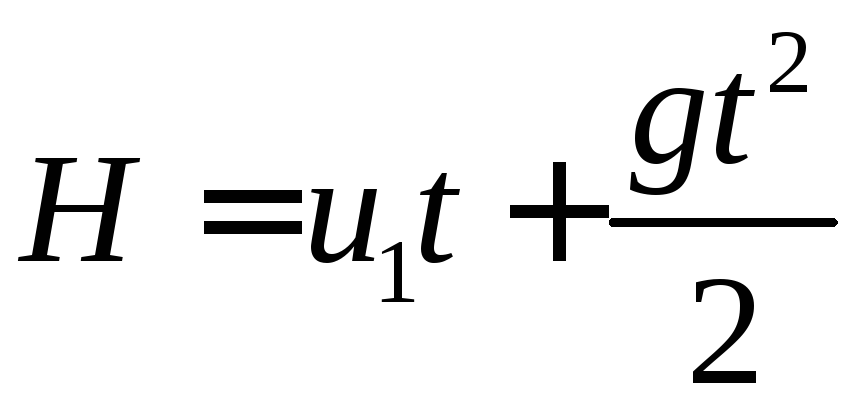
Знаходимо

= 35 м/с.

Тоді швидкість 2-ої частини снаряда

= 202 м/с;

Вектор швидкості буде направлений до горизонту під кутом

= 10^о.