Потенціальна енергія пружної деформації тіла.

Зовнішня сила, яка переміщує частини деформованого тіла, здійснює деяку роботу проти внутрішніх сил, які виникають в тілі під час деформації.

При деформаціях, для яких виконується закон Гука, можна вважати, що вся робота зовнішніх сил затрачається лише на збільшення потенційної енергії.

; ;

;

На таку ж величину змінюється потенціальна енергія розтягнутої пружини.

Густина енергії.

Енергія пружно деформованого тіла, що припадає на одиницю його об’єму: .

Елементи динаміки точки(тіла) змінної маси. Поняття про реактивний рух.

Одним із яскравих проявів закону збереження імпульсу є реактивний рух.

Реактивним рухом називається рух тіл, що виникає при відділенні від тіла частинки його маси або приєднанні до нього маси з деякою відносною швидкістю.

Реактивний рух – це рух, що виникає внаслідок зміни маси тіла, тобто рух тіла змінної маси М = М(t).

Приклади: ракетна техніка, приклади реактивного руху в природі демонстрації (сегнорове колесо, реакція витікання струменя води і т.д.)

Сила, яка виникає під час відділення або приєднання частинок речовини, яка діє на тіло змінної маси, називається силою реакції відділення або приєднання, тобто реактивною силою.

Реактивна сила може бути двох типів:

а) як результат відділення від тіла частини його маси;

б) як результат приєднання до тіла рухомої маси.

Загальні закони динаміки тіла (точки) змінної маси були відкриті і досліджені російськими вченими І.В. Мещерським та К.Е. Ціолковським – фундатором теоретичної космонавтики.

Основне рівняння динаміки точки змінної маси (рівняння Мещерського).

Розглянемо реактивний рух на прикладі руху ракети, моделюючи її матеріальною точкою змінної маси (рис. 3.5).

Зробимо деякі припущення:

а) нехай частинки газу, що відділяються від ракети з елементарною масою dМ взаємодіють з ракетою маси М тільки в момент їх безпосереднього контакту.

б) зміна маси ракети відбувається неперервно (без стрибків) – існування похідної .

в) швидкість вильоту газів із сопла відносно ракети стала і дорівнює .

Нехай в деякий момент часу t – маса ракети – М, а швидкість в нерухомій СВ – ; за елементарний проміжок часуdt відділена частинка маси (– dM) і імпульс ракети . За наступний проміжок часуdt маса ракети зменшиться і стане рівною , а її швидкість збільшиться до, тобто в момент часупісля викидання газів масоюімпульс системи

,

де враховано, що в нерухомій системі відліку маса викинутих газів має початкову швидкістьу напрямку руху ракети.

Рівнодійна всіх зовнішніх сил:

Рис. 3.5.

В момент відділення частинки між нею і ракетою починає діяти реактивна сила , що є внутрішньою силою системи ракета-частинка.

Обчислимо елементарну зміну імпульсу розглянувши системи за елементарний час dt:

або

Зміна імпульсу системи за час dt дорівнює імпульсу головного вектора зовнішніх сил:

або (3-14)

Одержане рівняння (3-14) носить назву рівняння Мещерського.

(3-15)

формула реактивної сили:

Реактивна сила залежить від відносної швидкості відділення (приєднання) частинок і від швидкості зміни маси тіла.

а) 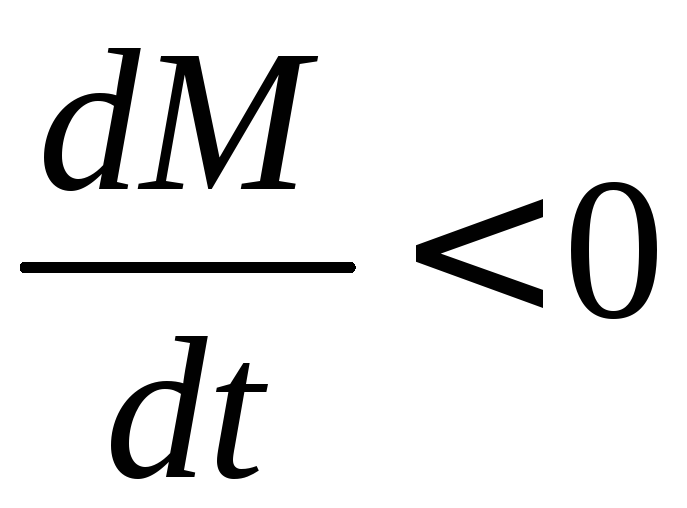– маса елементу – відділення;

б) 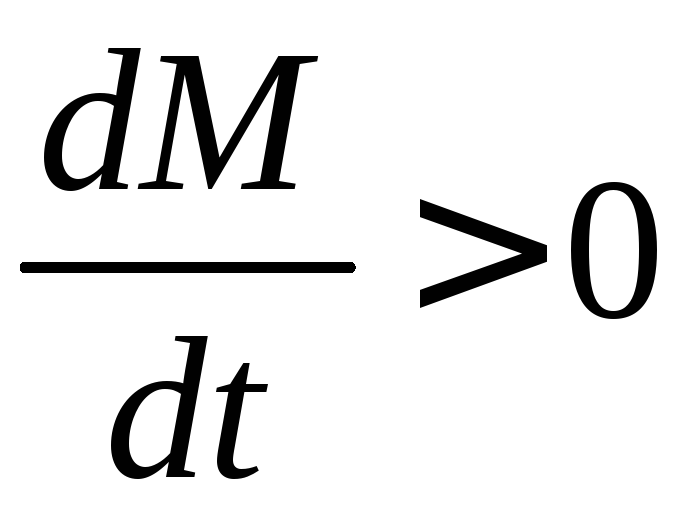– маса зростає – приєднання;

в) ;

Скорочена форма запису рівняння Мещерського

(3-16)