Пружні сили
Всі тверді тіла здатні під впливом зовнішніх сил змінювати свою форму чи об’єм, тобто деформуватися.
Тіла, в яких після припинення дії зовнішніх сил деформація повністю зникає, а початкова форма тіла та його об’єм повністю відновлюються, називаються абсолютно пружними, а сама деформація – пружною. В іншому випадку – непружною (пластичною). Властивість тіл відновлювати форму і об’єм після припинення дії зовнішніх сил називається пружністю.
Пружність – властивість багатьох твердих тіл і перш за все кристалічних. У природі не існує абсолютно пружних і абсолютно непружних тіл. Але багато речовин при малих або повільних деформаціях ведуть себе як абсолютно пружні – інші деформації незначні.
Внутрішні сили які виникають в пружних тілах при невеликих деформаціях називають пружними. Ці сили при усуненні зовнішніх сил повертають тілу його початкову форму та об’єм. Вони відносяться до фундаментальних електромагнітних взаємодій.
Типи пружної деформації.
Існує багато різноманітних пружних деформацій: одностороннє розтягування (стиснення), всебічне розтягування (стиснення), вигин, зсув, кручення та ін. Однак не всі типи деформацій є незалежними. Можна показати, що будь-яку пружну деформацію можна звести до сукупності двох деформацій, які називаються основними: розтягування (стиснення) та зсув.
Закон Гука в загальній формі.
При будь-якій деформації в тілі виникають пружні сили.
В 1675р. англійський фізик, сучасник Ньютона, Роберт Гук з’ясував, що величина і напрям сил пружності залежать як від типу, так і від величини деформації.
Формулювання:
а) при
будь-якій малій деформації сила пружності
прямо пропорційна величині деформації
і направлена в сторону, протилежну
переміщенню частинок речовини:
;
б) малі
деформації тіла прямо пропорційні
прикладеним зовнішнім силам
.
Закон Гука для різноманітних деформацій.
а) деформація одностороннього розтягування (стиснення) (рис. 3.1).
Характеристики деформації:
Абсолютне
видовження
;
|
|
|
Рис. 3.1. |
Сила пружності, що виникає в розтягненому стержні оцінюється по зовнішній силі.
З умови рівноваги:
;
;
–коефіцієнт
пружності, який характеризує властивості
даного матеріалу.
–зусилля
або механічне напруження – зовнішня
сила, прикладена до одиниці площі.
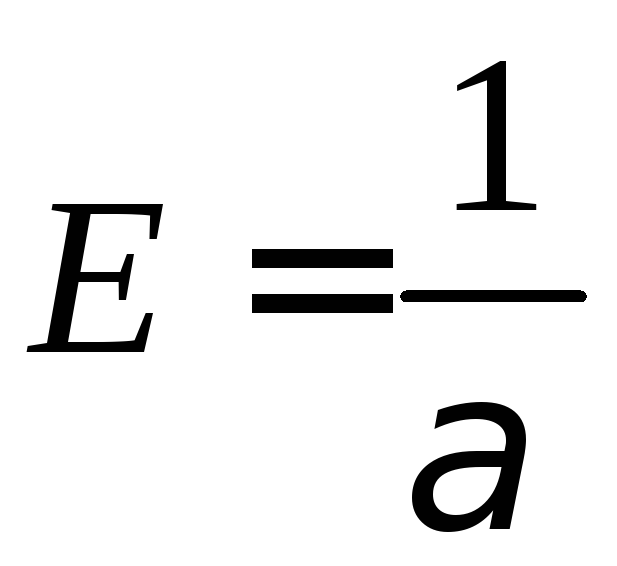–модуль
Юнга.
(3-11)
;
В границях
пружної деформації :
.
Відносне подовження прямо пропорційне зусиллю.
;
,
де
;
(3-12)
Знак
«–» вказує на те, що напрямок сили
пружності протилежний напрямку
розтягування (тобто деформації).
називається коефіцієнтом сили пружності
або просто пружністю (жорсткістю).
Фізичний зміст модуля Юнга:
,
,
то
Модуль Юнга чисельно дорівнює механічному напруженню (зусиллю), яке викликає відносне видовження рівне одиниці, тобто зусиллю, яке розтягує (стискає) предмет вдвічі. Окрім каучуку жоден матеріал не витримує такого розтягування; матеріал розривається при значно менших розтягуваннях.
;
(3-13)
При малих деформаціях напруження, що виникає всередині тіла прямо пропорційне відносній деформації.
(Демонстрація розтягування гумового шнура або трубки).