Закони збереження й перетворення механічної енергії консервативних систем.

Молекула розпадається на два атоми. Маса одного з атомів в n = 3 рази більше, ніж другого. Нехтуючи початковою кінетичною енергією та імпульсом молекули, визначити кінетичні енергії таатомів, якщо їх сумарна кінетична енергіяЕ = 0,032 нДж.
На рейках стоїть платформа, на якій у горизонтальному положенні закріплена гармата без противіткатного пристрою. Із гармати роблять постріл уздовж залізничного шляху. Маса снаряду дорівнює 10 кг та його швидкість=1 км/с. Масаплатформи з гарматою та іншим вантажем дорівнює 20 т. На яку відстаньl відкотиться платформа після пострілу, якщо коефіцієнт опору f = 0,002?
В балістичний маятник масою М = 5 кг попала куля масою = 10 кг і застрягла у ньому. Знайти швидкістькулі, якщо маятник, відхилившись після удару, піднявся на висотуh = 10 см.
Два вантажі масами = 10 кг та= 15 кг підвішені на нитках довжиноюl = 2 м так, що вантажі доторкаються між собою. Менший вантаж був відхилений на кут = 60^о та відпущений. Визначити висоту h, на яку піднімуться обидва вантажі після удару. Удар вантажів вважати не пружним.
Дві не пружні кулі масами = 2 кг та= 3 кг рухаються зі швидкостями відповідно= 8 м/с та= 4 м/с. Визначити збільшеннявнутрішньої енергії куль при їх зіткненні в двох випадках: 1) менша куля доганяє більшу; 2) кулі рухаються на зустріч одна одній.
Куля масою , летить зі швидкістю= 5 м/с, ударяє рухому кулю масою. Удар прямий, не пружний. Визначити швидкістькуль після удару, а також частку кінетичної енергії кулі, що летить, яка пішла на збільшення внутрішньої енергії цих куль. Розглянути два випадки: 1)= 2 кг,= 8 кг; 2)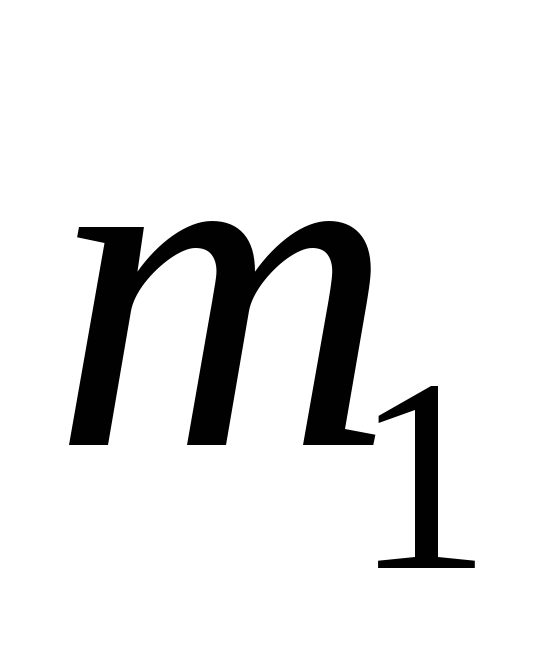= 8 кг,= 2 кг.
Молотом масою 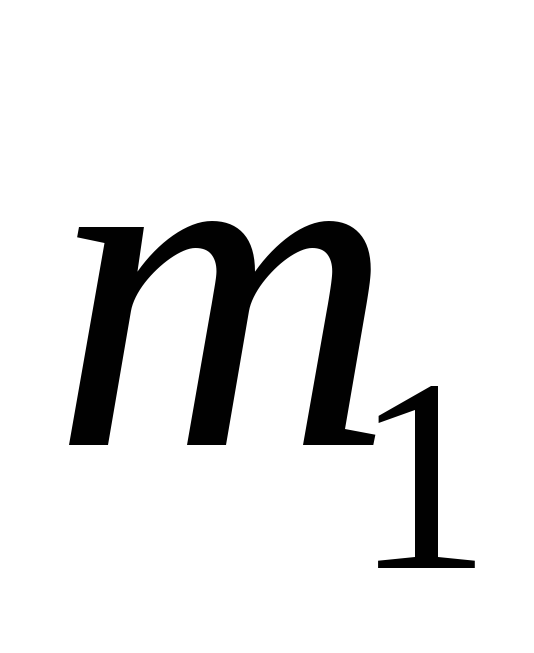= 5 кг, б’ють невеликий шматок заліза, який лежить на наковальні. Масанаковальні дорівнює 100 кг. Масою шматка заліза знехтувати. Удар не пружний. Визначити ККД удару молота при заданих умовах.
Бойок спайного молота масою 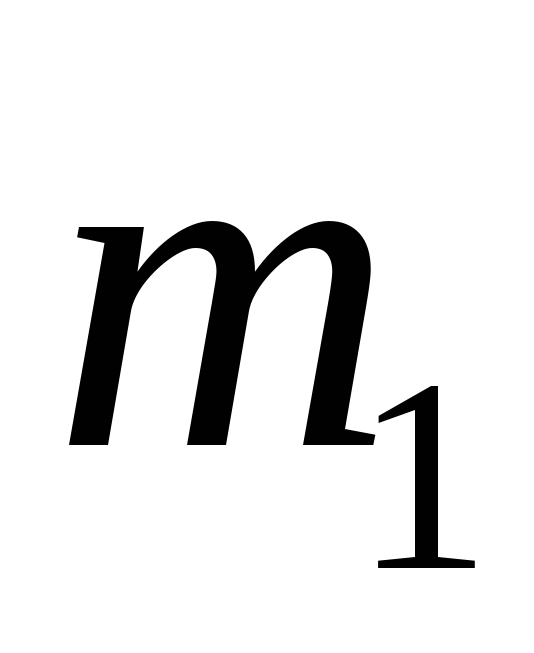= 500 кг падає з деякої висоти на палю масою= 100 кг. Знайти ККД удару бойка, вважаючи його не пружним. Зміною потенціальної енергії палі при заглибленні знехтувати.
Молотком, маса якого = 1 кг, забивають у стіну цвях масою= 75 г. Визначити ККД удару молотка за заданими умовами.
Куля масою = 200 г, рухається зі швидкістю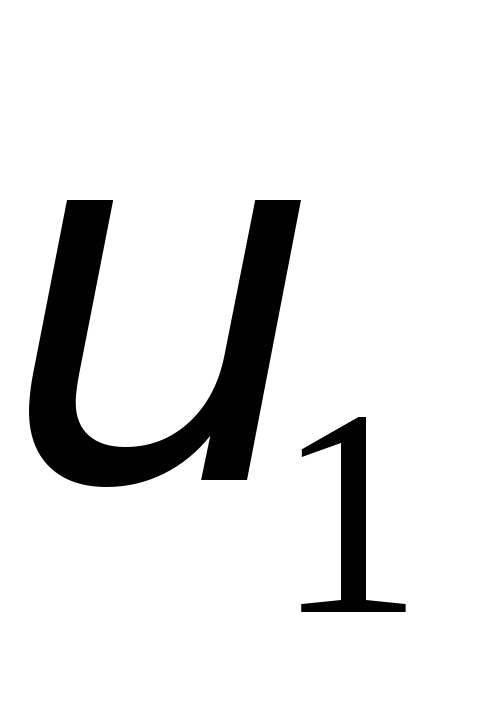= 10 м/с, вдаряє нерухому кулю масою= 800 г. Удар прямий, абсолютно пружний. Які будуть швидкості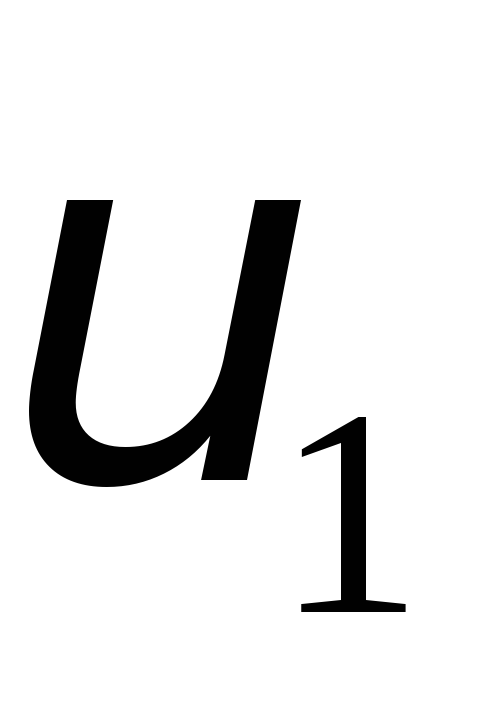такуль після ударів?

Елементи динаміки тіла (точки) змінної маси

Ракета стартовою масою М₀ = 10³ кг запущена з поверхні Землі піднімається вертикально вгору з прискоренням а = 2g. Відносна швидкість витікання продуктів згорання = 1200 м/с. Час повного згорання палива t = 8 с. Знайти витрату ракетного палива μ та його масу М_п.
Яку частину стартової маси одноступінчастої ракети повинна складати маса палива, якщо цю ракету потрібно вивести на колову орбіту Землі. Швидкість витікання газів із сопла ракети взяти рівною 4000 м/с.
Ракета рухається в однорідному полі сили тяжіння вгору з постійним прискоренням . Нехтуючи опором атмосфери і вважаючи ефективну швидкістьвитікання газів постійною, визначити час, за який маса ракети зменшиться в два рази.
Ефективна швидкість витікання газів з ракети = 2,4 км/с. Яке повинне бути відношення запаса палива до ваги ракети без палива, щоб після згорання палива ракета, яка рухається поза полем тяжіння та поза атмосферою, набула б швидкості 9 км/с.
Ракета рухається поступально при відсутності тяжіння та опору атмосфери. Ефективна швидкість витікання газів 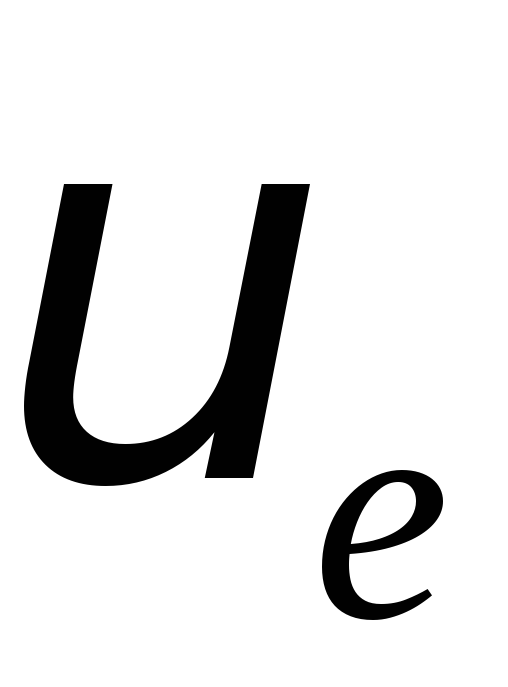= 2400 м/с. Визначити число Ціолковського, якщо в момент повного згорання палива швидкість ракети буде рівною 4300 м/с.
Тіло змінної маси, з початковою швидкістю, яка рівна нулю, рухається з постійним прискоренням по горизонтально розташованим направляючим. Ефективна швидкість витікання газівпостійна. Визначити, нехтуючи опором, шлях, який пройшло тіло до момента, коли його маса зменшиться в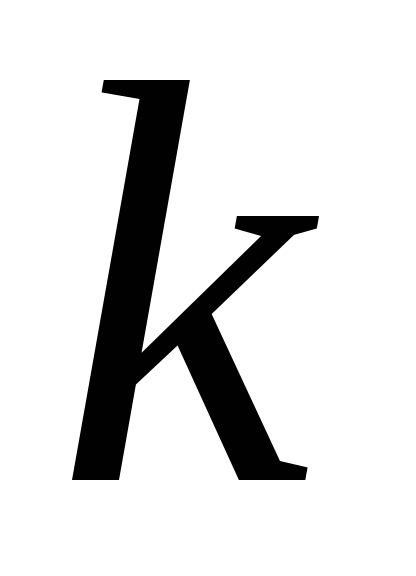разів.
Ефективні швидкості витікання у першій та другій ступіні в двухступінчатій ракеті відповідно дорівнюють 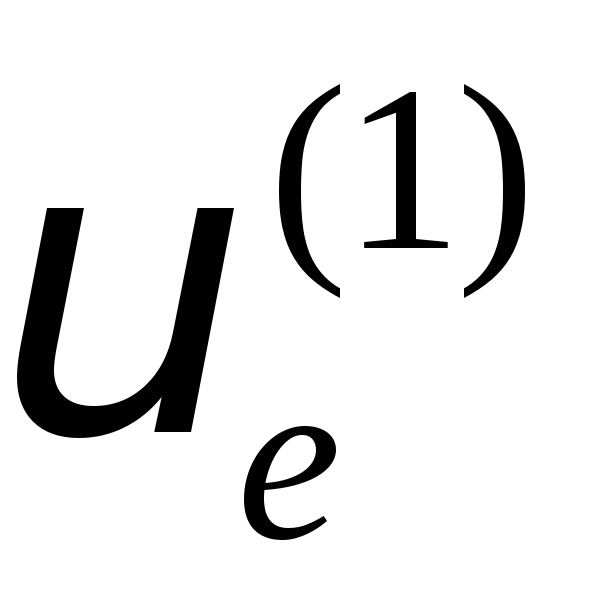= 2400 м/с та= 2600 м/с. Визначити, вважаючи, що рух відбувається поза полем тяжіння і атмосфери, числа Ціолковського для забезпечення кінцевої швидкості = 2400 м/с першої ступіні та кінцевої швидкості= 5400 м/с другої ступіні.
Чотирьохступінчата ракета складається з чотирьох ракет. Конструктивна характеристика і ефективна швидкістьу всіх ракет однакові і рівні= 4,7,= 2,4 км/с. Якою повинна бути стартова вага ракети, щоб вона вантажу масою 1 т надала швидкості= 9000 м/с?
Ракета стартує з Місяця вертикально до його поверхні. Ефективна швидкість витікання газів = 2000 м/с. Число Ціолковського рівне 5. Визначити, який повинен бути час згорання палива, щоб ракета досягла швидкості= 3000 м/с (вважати, що прискорення сил тяжіння поблизу Місяця рівне 1,62 м/с²).
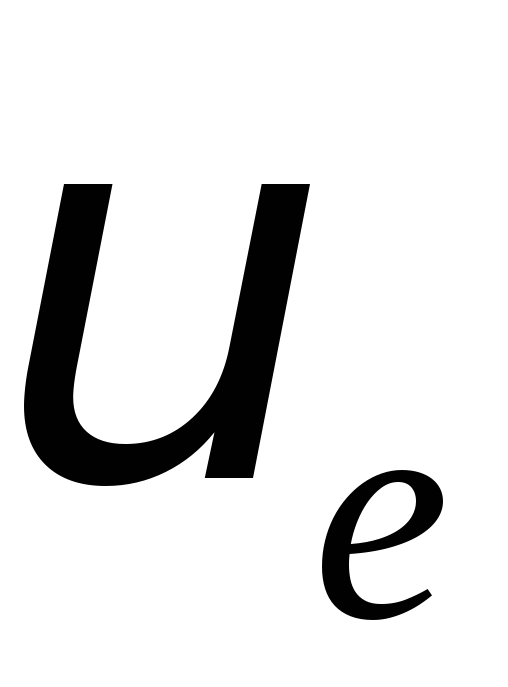Ракета з початковою масою піднімається вертикально вгору в однорідному полі сили тяжіння з постійним прискоренням(– прискорення земного тяжіння). Нехтуючи опором атмосфери і вважаючи ефективну швидкістьвитікання газів постійною, визначити: 1) закон зміни маси ракети; 2) закон зміни маси ракети при відсутності поля тяжіння.