Задачі для самостійного розв’язування та домашнього завдання

Тіло масою = 2 кг рухається зі швидкістю= 3 м/с та доганяє тіло масою= 8 кг, яке рухається зі швидкістю= 1 м/с. Вважаючи удар центральним, знайти швидкостітатіл після удару, якщо удар: а) не пружний; б) пружний.
Яке повинно бути співвідношення між масами татіл попередньої задачі, щоб при пружному ударі перше тіло зупинилося?
Тіло, яке рухається з масою ударяється в нерухоме тіло масою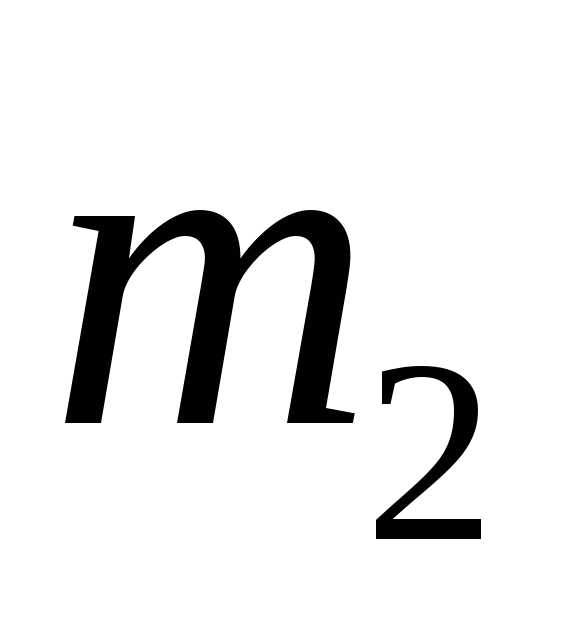. Вважаючи удар пружним та центральним, знайти, яка частина кінетичної енергіїперше тіло передає другому при ударі. Задачу розв’язати спочатку у загальному вигляді, а потім розглянути випадки: 1); 2).
Тіло, масою яке рухається та ударяється в нерухоме тіло масою. Яким повинно бути відношення мас, щоб при центральному пружному ударі швидкість першого тіла зменшилася в 1,5 рази? З якою кінетичною енергієюпочне рухатись при цьому друге тіло, якщо початкова кінетична енергія першого тіла= 1 кДж ?
Нейтрон (маса 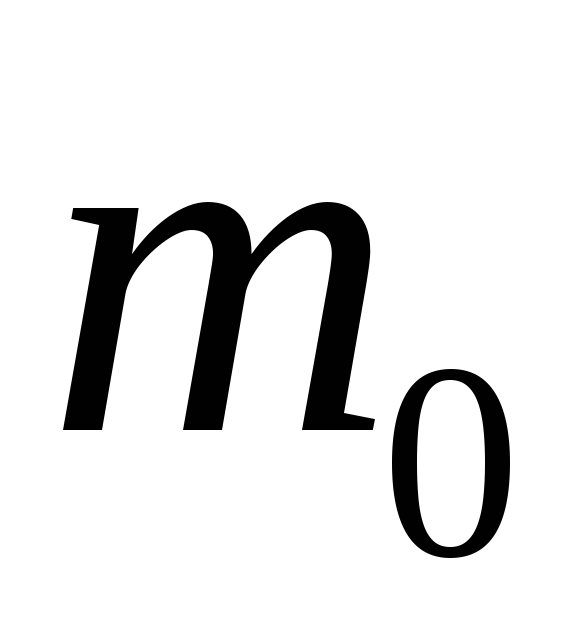) ударяється в нерухоме ядро атома вуглецю (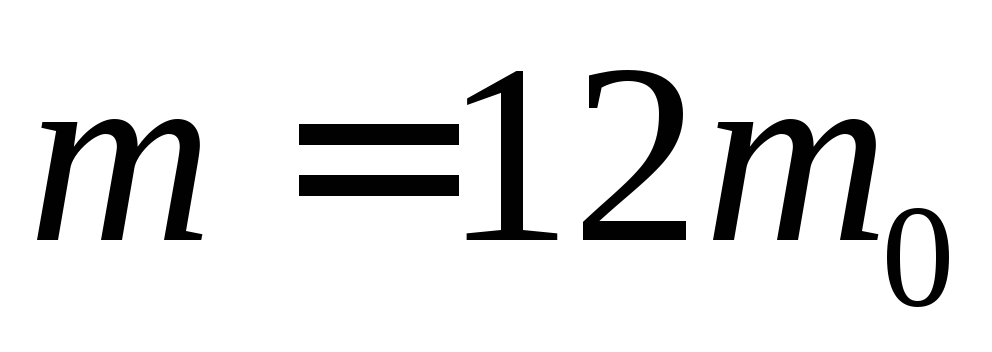). Вважаючи удар центральним та пружним, знайти, у скільки разів зменшиться кінетична енергіянейтрона при ударі.
Нейтрон (маса ) ударяється в нерухоме ядро: а) атома вуглецю (); б) атома урану (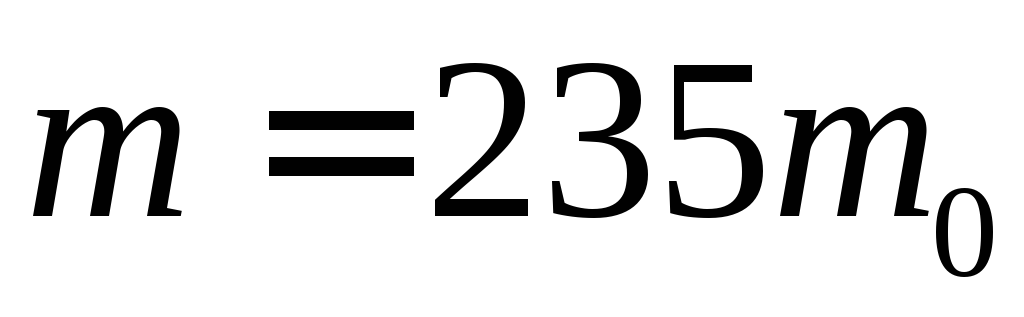). Вважаючи удар центральним та пружним, знайти, яку частину швидкостізагубить нейтрон при ударі.
Камінь кинули вверх під кутом = 60^о до площини горизонту. Кінетична енергія камня в початковий момент часу дорівнює 20 Дж. Визначити кінетичнуТ та потенціальну П енергії камня у найвищій точці його траєкторії. Опором повітря знехтувати.
З якої найменшої висоти h повинен починати скочуватись акробат на велосипеді (не працюючі ногами), щоб проїхати по доріжці, яка має форму «Мертвої петлі» радіусом R = 4 м , та не відірватись від доріжки у верхній точці петлі? Тертям знехтувати.
Тіло ковзає з найвищої точки купола, який має форму папівсфери. Яку дугу опише тіло, перш ніж відірветься від поверхні купола? Тертям знехтувати.
При пострілі із гармати снаряд масою = 10 кг отримує кінетичну енергію= 1,8 МДж. Визначити кінетичну енергіюствола гармати в результаті віддачі, якщо маса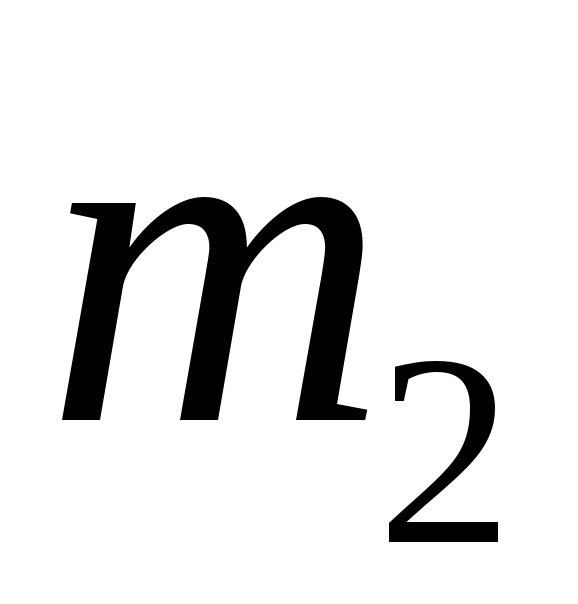ствола гармати дорівнює 600 кг.
Ядро атома розпадається на два осколки масами 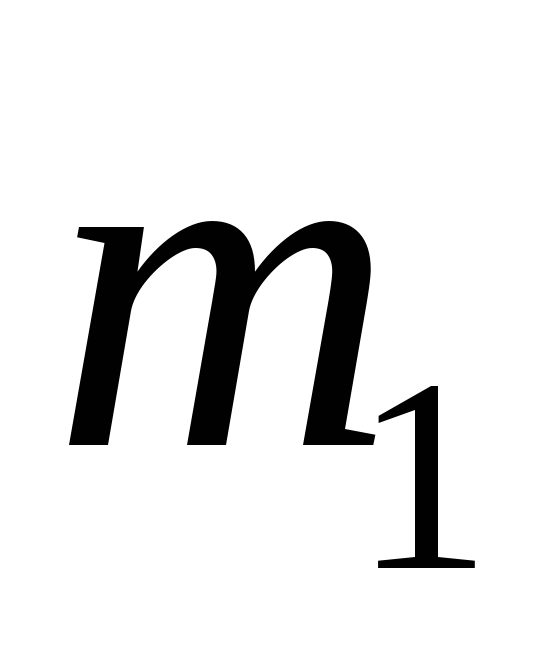= 1,6·10^-25 кг та = 2,4·10^-25 кг. Визначити кінетичну енергію другого осколка, якщо енергіяпершого осколка дорівнює 18 нДж.
Ковзаняр, стоячи на льоду, кинув вперед гирю масою = 5 кг та в результаті віддачі покотився назад зі швидкістю= 1 м/с. Маса ковзаняра= 60 кг. Визначити роботуА, виконану ковзанярем при киданні гирі.
Велосипедист повинен проїхати по треку “мертва петля”. Якою повинна бути мінімальна висота похилої площини, щоб скочуючись з неї в “петлю” велосипедист, не працюючи педалями не відірвався б від неї у верхній точці? Радіус петлі R.
В одного автомобіля маса вдвічі більша, а кінетична енергія вдвічі менша, ніж у другого. А коли кожен з автомобілів збільшив швидкість на 30 км/год, їхні кінетичні енергії зрівнялися. Знайти початкові швидкості автомобілів.
Куля масою = 1,8 кг зіткнулася з кулею більшої масиМ, яка перебуває у стані спокою. У результаті прямого пружного удару куля втратила 0,36 своєї кінетичної енергії . Визначити масу більшої кулі.
З двох абсолютно пружних куль, які зіткнулися, більша куля перебувала у стані спокою. У результаті прямого удару менша куля втратила 3/4 своєї кінетичної енергії . Визначити відношеннямас куль.