Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский финансово-промышленный университет Синергия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

matem-ege-shpora / Математика формулы.pdf

Скачиваний:

Добавлен:

03.06.2015

Размер:

2.28 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 306 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

http://vk.com/ege100ballov

2.Аналитическая геометрия

2.1.Прямая на плоскости.

Общее уравнение прямой: Ax + By + C = 0.

Уравнение прямой в параметрической форме (t – параметр):

x = kxt + x0, y = kyt + y0, kx2 + ky2 ≠ 0.

Уравнение прямой с угловым коэффициентом k:

y = kx + b, k = tg α, α (0; π2) (π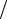2 ; π) — угол наклона прямой.

Уравнение прямой в отрезках:	x	+ y = 1, (a ≠ 0, b ≠ 0), (a; 0) и (0; b) — коорди-
	a	b
наты точек пересечения прямой с осями Ox и Oy соответственно.
Нормальное уравнение прямой:	x cos α + y sin α – p = 0, где p — расстояние

от начала координат до прямой, α — угол между положительным направлением оси Ox и перпендикуляром к прямой, опущенным из начала координат. Коэффициенты нормального уравнения прямой связаны с коэффициентами общего уравнения равенствами:

cos α = A,

sin α = B,

− p

= C ,

λ =

A2 + B2

где λ — нормирующий множитель уравнения. Знак λ противоположен знаку C.

Уравнение прямой, проходящей через две заданные точки (x1,

y1)

и (x2, y2):

y − y1

x − x1

− y

− x

Расстояние d от точки (x0, y0) до прямой Ax + By + C = 0:

d =

| Ax0

+ By0

+ C |

A2 + B2

Необходимое и достаточное условие принадлежности трех

точек (x1, y1), (x2, y2),

(x3, y3)

одной прямой:

= 0 .

x3 y3 1

Координаты точки (x0, y0), делящей отрезок с концами (x1, y1), (x2, y2) в отношении

λ ≠ –1:

x1 + λx2

y1 + λy2

1 + λ

+ λ

Координаты точки пересечения двух прямых A1x + B1y + C1 = 0, A2x + B2y + C2 = 0

определяется по формулам Крамера:

B2 C2

C2 A2

Необходимое и достаточное условие параллельности прямых: A1B2 – A2B1 = 0. Необходимое и достаточное условие перпендикулярности прямых: A1A2 + B1B2 = 0.

http://vk.com/ege100ballov

II.2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

Координаты точки пересечения прямых y = k1x + b,

y = k2x + b:

x =

b2 − b1

k1b2 − b1k2

k1 − k2

Необходимое и достаточное условие параллельности прямых:

k1 = k2.

Необходимое и достаточное условие перпендикулярности прямых:

k1k2 = –1.

AB − A B |

Угол

α между прямыми:

sin α =

A2 + B2

| A A + BB |

AB − A B

cos α =

1 2

tg α =

1 2

+ B2

A1A2 + B1B2

Угол

α между прямыми y = k1x + b, y = k2x + b:

k1 − k2

tg α =

( k k ≠ –1).

Если

k k

= –1,

то α = π/2.

1 + k1k2

Уравнение пучка прямых,

проходящих через точку пересечения прямых Aix + Biy +

+ Ci = 0 (I = 1, 2): λ1(A1x + B1x + C1) + λ2(A2x + B2x + C2) = 0 ( λ21 + λ22 ≠ 0 ).

Условие пересечения трех прямых Aix + Biy + Ci = 0

(I = 1, 2, 3) в одной точке:

A1 B1 C1

A2 B2 C2 = 0.

A3 B3 C3

2.2. Плоские линии второго порядка. Эллипс. Гипербола. Парабола.

Общее уравнение линии второго порядка в декартовой системе координат:

F (x, y) / a11x2 + 2a12xy + a22y2 + 2a1x + 2a2y + a0 = 0.

(1)

Инварианты относительно переноса начала координат и поворота осей:

S = a11 + a22; δ =

a11 a12

;

∆ =

a11

a12

a a a

a12 a22

Характеристическая квадратичная форма уравнения (1):

a11x2 + 2a12xy + a22y2.

(2)

Характеристическое уравнение квадратичной формы (2):

a11 − λ

a12

= 0.

− λ

Связь между корнями характеристического уравнения квадратичной формы и инвариан-

тами: S = λ1 + λ2; δ = λ1 λ2.

Полуинвариант уравнения (1) (инвариант относительно поворота осей):

A =	a22	a2	+	a11 a1		.
A =	a22	a2	+	a11 a1		.
	a	a		a	a
	2	0		1	0

В зависимости от значений величин δ, ∆, S, A уравнение (1) определяет одну из следующих линий:

	∆ ≠ 0	S ∆ < 0	действительный эллипс;
δ > 0	∆ ≠ 0	S ∆ > 0	мнимый эллипс;
δ > 0		S ∆ > 0	мнимый эллипс;
	∆ = 0	пара мнимых сопряженных пересекающихся прямых;
	∆ = 0	пара мнимых сопряженных пересекающихся прямых;

http://vk.com/ege100ballov

2.2. ПЛОСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА. ЭЛЛИПС. ГИПЕРБОЛА. ПАРАБОЛА.					17
δ < 0	∆ ≠ 0		гипербола;
δ < 0		∆ = 0	пара действительных пересекающихся прямых;
		∆ = 0	пара действительных пересекающихся прямых;
	∆ ≠ 0		парабола;
			A > 0	пара мнимых параллельных прямых;
δ = 0			A > 0	пара мнимых параллельных прямых;
δ = 0		∆ = 0		пара действительных параллельных прямых;
		∆ = 0	A < 0	пара действительных параллельных прямых;
				пара действительных совпадающих прямых.
			A = 0	пара действительных совпадающих прямых.

Ортогональным преобразованием координат

x = x ′ cos α – y ′ sin α + x0, y = x ′ sin α + y ′ cos α + y0

общее уравнение F (x, y) = 0 в невырожденном случае (∆ ≠ 0) приводится к канонической форме уравнений эллипса, гиперболы и параболы.

Э л л и п с . Каноническое уравнение:

x2	y2		a2		∆		b2 = −	∆
a2 +		= 1,		= −		,			,
	b2				λ2δ			λ1δ
где λ1 и λ2 — корни характеристического уравнения,							λ1.λ2.

Уравнение в параметрической форме (t — параметр):

x = a cos t,

y = b sin t,

(t [0; 2π)).

Уравнение в полярных координатах r,

r =

где p = b

a — фокаль-

1 + e cos ϕ

ный параметр, e = a2 − b2

a — эксцентриситет (0 ≤ e < 1), a — большая полуось.

Уравнение директрис эллипса в декартовой системе координат:

x = – a/e,

x = a/e.

О к р у ж н о с т ь .

Уравнение окружности радиуса R,

с центром в начале координат: x2 + y2 = R2 ;

с центром в точке (a; b):

(x – a)2 + (y – b)2 = R2 ;

с центром в точке (r0; n):

r2 – 2rr0 cos (n – n0) + r02 = R2 ;

с центром в полюсе полярной системы координат:

r = R ;

Г и п е р б о л а .

Каноническое уравнение:

∆

, b2 =

∆

a2 −

= 1,

= −

λ2δ

λ1δ

где λ1 и λ2 — корни характеристического уравнения,

λ1.λ2.

Уравнение в параметрической форме (t

— параметр):

x = a ch t, y = b sh t, (t (– ∞; + ∞)).

Уравнение в полярных координатах r,

r =

p = b a — фокальный

1 + e cos ϕ

параметр, e = a2 − b2 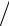a > 1 — эксцентриситет.

Уравнение директрис гиперболы в декартовой системе координат: x = – a/e, x = a/e.

http://vk.com/ege100ballov

18	II.2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

П а р а б о л а .

	2	p =	1	−	∆
Каноническое уравнение: y	= 2px,						— фокальный параметр.
			S		S
				r =			p
Уравнение параболы в полярных координатах:								.
						1 + cos ϕ

2.3. Плоскость.

Общее уравнение плоскости в декартовой системе координат:

Ax + By + Cz + D = 0,					A2 + B2 + C2 ≠ 0.
Уравнение в отрезках:	x	+ y	+ z	= 1,	(abc ≠ 0) ;
	a	b	c

(a; 0; 0), (0; b; 0), (0; 0; c) — точки пересечения плоскости с осями Ox, Oy и Oz соответственно.

Нормальное уравнение: x cos α + y cos β + z cos γ – p = 0, где cos α, cos β и

cos γ — компоненты вектора единичной длины, перпендикулярного плоскости, p — расстояние от начала координат до плоскости.

Коэффициенты общего и нормального уравнений плоскости связаны равенствами:

cos α = λA, cosβ = λB,

cos γ = λC,

p = −λD,

A2 + B2 + C2

(знак λ противоположен знаку D).

Параметрическое уравнение плоскости, проходящей через точку (x0, y0, z0) и содержа-

щей неколлинеарные векторы a = (a1; a2; a3)

b = (b1; b2; b3) (u, v — параметры):

x = x0 + a1u + b1v, y = y0 + a2u + b2u, z = z0 + a3u + b3v.

Компоненты векторов

и b

связаны с коэффициентами A, B, C:

A =

a2 a3

B =

a3 a1

, C =

a1 a2

Уравнение плоскости, проходящей через три заданные точки

(xi; yi; zi) (i = 1, 2, 3), не

лежащие на одной прямой:

= 0 .

x3 y3 z3 1

Уравнение плоскости, проходящей через заданную точку (x0,

y0, z0)

и перпендикулярной

вектору n = (A; B; C): A(x – x0) + B(y – y0) + C(z – z0) = 0.

Необходимое и достаточное условие параллельности плоскостей Aix + Biy + Ciz +

+ Di = 0 (i = 1, 2): A1 = λA2, B1 = λB2, C1 = λC2 .

Необходимое и достаточное условие перпендикулярности плоскостей:

A1 A2 + B1B2 + C1C2 = 0.

Расстояние от точки (x0; y0; z0) до плоскости Ax + By + Cz + D = 0:

d =	Ax0	+ By0	+ Cz0	+ D	.
	Ax0	+ By0	+ Cz0	+ D

		A2 + B2 + C2
		A2 + B2 + C2

<<< < Предыдущая 1 2 3 4 56 / 306 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в папке matem-ege-shpora

#
03.06.20151.37 Кб17README.txt
#
03.06.20151.1 Mб31математика С1.pdf
#
03.06.20154.5 Mб42математика С2.pdf
#
03.06.20151.89 Mб31математика С3.pdf
#
03.06.20152.19 Mб87математика С4.pdf
#
03.06.20152.28 Mб35Математика формулы.pdf
#
03.06.20151.21 Mб25Математика формулы1.pdf
#
03.06.20152.9 Mб87Математика шпаргалка.pdf