Теорема Чебишева

Теорема Чебишева. Якщо послідовність попарно незалежних випадкових величин Х, Х, ... , Х, ... має скінченні математичні сподівання і дисперсії цих величин рівномірно обмежені (не перевищують сталого числаC), то середнє арифметичне випадкових величин збігається по ймовірності до середнього арифметичного їх математичних сподівань, тобто якщо – будь-яке додатне число, то

Зокрема, середнє арифметичне послідовності попарно незалежних величин, дисперсії яких рівномірно обмежені і які мають одне і те ж математичне сподівання a, збігається по ймовірності до математичного сподівання a, тобто якщо – будь-яке додатне число, то

108. Послідовність незалежних випадкових величин Х, Х, ... , Х, ... задана законом розподілу

Хa– a

р n/(2n + 1) (n + 1)/(2n + 1)

Чи застосовна до заданої послідовності теорема Чебишева?

109. Послідовність незалежних випадкових величин Х, Х, ... , Х, ... задана законом розподілу

Х п + 1 – n

p п/(2n + 1) (n + 1)/(2n + 1)

а) Переконатися, що вимога теореми Чебишева про рівномірну обмеженість дисперсій не виконується;

б) чи можна звідси зробити висновок, що до даної послідовності теорема Чебишева незастосовна?

Функція і густина розподілу ймовірностей випадкових величин Функція розподілу ймовірностей випадкової величини

Функцією розподілу називають функцію , що визначає для кожного значення ймовірність того, що випадкова величина набуде значення, менше , тобто

Часто замість терміну «функція розподілу» використовують термін «інтегральна функція ».

111. Випадкова величина X задана функцією розподілу

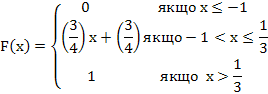
Знайти ймовірність того, що в результаті випробування величина набуде значення, яке міститься в інтервалі (0,1/3).

Розв’язання. Ймовірність того, що набуває значення із інтервалу (,), рівна приросту функції розподілу на цьому інтервалі:

Поклавши =0, отримаємо

_x=1/3 – _x=0 = 1/4

112. Випадкова величина X задана на всій осі Ох функцією розподілу . Знайти ймовірність того, що в результаті випробування величина X набуде значення із інтервалу (0 , 1).

113. Випадкова величина X задана функцією розподілу

Знайти ймовірність того, що в результаті випробування величина X набуде значення із інтервалу (-1, 1).

114. Випадкова величина X задана на всій осі Ох функцією розподілу

. Знайти можливе значення , що задовольняє умові: з ймовірністю 1/6 випадкова величина X в результаті випробування набуде значення більше за .

115. Дискретна випадкова величина задана законом розподілу

X	3	4	7	10
P	0.2	0.1	0.4	0.3

Знайти функцію розподілу і побудувати її графік.

Густина розподілу ймовірності неперервної випадкової величини.

Густиною розподілу ймовірності неперервної випадкової величини називають першу похідну від функції розподілу:

Часто замість терміну «густина розподілу» використовують терміни «густина ймовірності» і «диференціальна функція». Ймовірність того, що неперервна випадкова величина X набуде значення, що належить інтервалу (), визначається рівністю

За відомою густиною розподілу можна знайти функцію розподілу

116. Задана функція розподілу неперервної випадкової величини X.

Знайти густину розподілу f(x).

Розв’язання. Густина розподілу дорівнює першій похідній від функції розподілу:

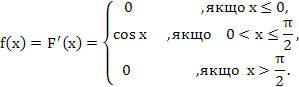
Відмітимо, що при х=0 похідна не існує.

117. Задана функція розподілу неперервної випадкової величини X:

Знайти густину розподілу f(x).

118. Неперервна випадкова величина X задана густиною розподілу в інтервалі; поза цим інтервалом f(x)= 0. Знайти ймовірність того, що X набуде значення, що належить інтервалу .

119. Задана густина розподілу неперервної випадкової величини X:

Знайти функцію розподілу F(х).

120. Задана густина розподілу неперервної випадкової величини X:

Знайти функцію розподілу F(х).

121. Задана густина розподілу неперервної випадкової величини X:

Знайти функцію розподілу F(х).

122. Задана густина розподілу неперервної випадкової величини X:

Знайти функцію розподілу F(x).

123. Густина розподілу неперервної випадкової величини X задана на всій осі Ох рівністю . Знайти сталий параметр .

Розв’язання. Густина розподілу повинна задовольняти умові

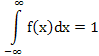
Будемо вимагати, щоб ця умова виконувалася для заданої функції

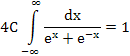
Звідси

(1)Знайдемо спочатку невизначений інтеграл:

Потім обчислимо невласний інтеграл:

Таким чином,

(2)Підставивши (2) у (1), остаточно отримаємо = 1/2.

124. Густина розподілу неперервної випадкової величини X задана на всій осі Ох рівністю . Знайти сталий параметр .

125. Густина розподілу неперервної випадкової величини X в інтервалі дорівнює поза цим інтервалом . Знайти сталий параметр .

126. Густина розподілу неперервної випадкової величини X задана в інтервалі (0, 1) рівністю поза цим інтервалом . Знайти сталий параметр .