Пример 10. Найдите решения задачи Штурма - Лиувилля (задание 8)

(1)

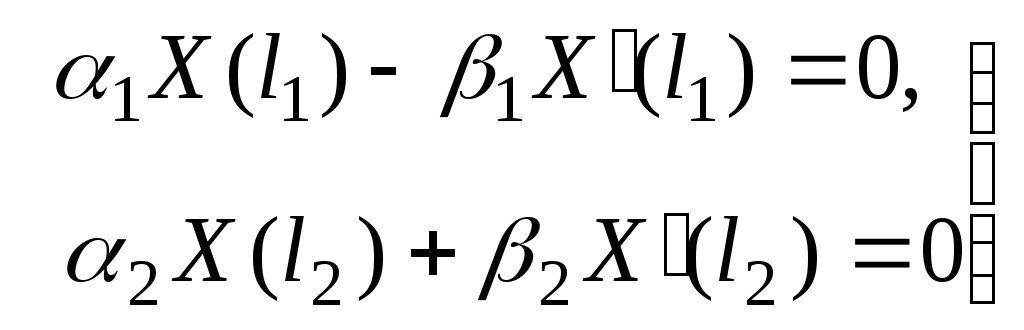(2)

№
1	2	3	1	0	1	0
2	3	4	1	0	0	1
3	1	3	1	2	3	4

Решение. Общее решение уравнения (1) при имеет вид

. (3)

Это решение должно удовлетворять граничным условиям (2)

(4)

Однородная система имеет ненулевые решения, если её определитель равен нулю. Находим определитель этой системы, приравниваем его нулю и получаем уравнение

, (5)

называемое характеристическим уравнением задачи Штурма – Лиувилля. Пусть корни уравнения (5). Тогда решение системы (4) будет равно

.

При , получаем

.

Решения уравнения (1) в этом случае будут иметь вид

. (6)

Если решения системы (4) представить в виде

,

то решения уравнения (1) будут иметь вид

. (7)

Рассмотрим заданные варианты задачи Штурма - Лиувилля.

Вариант первый

№
1	2	3	1	0	1	0

Задача (1) − (2) для этих параметров

будет иметь характеристическое уравнение .Корни этого уравнения (собственные значения задачи Штурма - Лиувилля) в данном случае равны

Решения задачи Штурма - Лиувилля (собственные функции) согласно выражениям (6), (7) можно представить в виде

.

Вариант второй

№
2	3	4	1	0	0	1

Задача Штурма - Лиувилля для этих параметров

будет иметь характеристическое уравнение

,

собственные значения

и собственные функции

или

.

Вариант третий

№
3	1	3	1	2	3	4

Задача Штурма - Лиувилля для этих параметров

будет иметь характеристическое уравнение

.

Первые пять корней характеристического уравнения приведены в следующей таблице:

	1	2	3	4	5
	0,5068	3,5688	11,0692	23,4325	40,7144

Собственные функции, соответствующие найденным собственным значениям

или

.

Пример 11. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в круге

, , ,

.

Решение. В полярных координатах задача примет вид

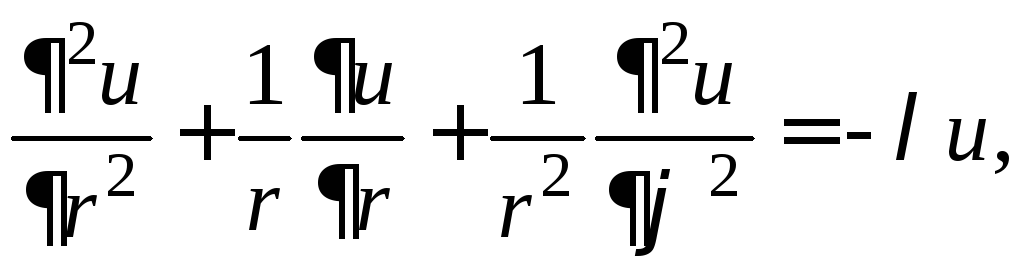(1)

. (2)

Решение этой задачи найдём с помощью метода Фурье. Для этого положим . Тогда уравнение (1) примет вид

или

.

Левая часть полученного равенства не зависит от , а правая – от . Это возможно в том случае, когда они равны постоянной . В результате приходим к двум краевым задачам

, , (3)

, . (4)

Решение задачи (3) представляет собой систему функций

В таком случае задача (4) примет вид

, (5)

. (6)

Уравнение (5) представляет собой уравнение Бесселя, а задача (5) – (6) называется краевой задачей на собственные значения для уравнения Бесселя. Общее решение уравнения (5), как известно, определяется выражением

,

где – цилиндрическая функция первого рода -го порядка (функция Бесселя), – цилиндрическая функция второго рода (функция Неймана). Из условия, что решение должно быть ограниченным, следует положить B_n=0, так как при . Искомое решение приобретает вид

.

Чтобы определить собственные значения , воспользуемся граничным условием (6). В результате получаем характеристическое уравнение . Это уравнение имеет счетное множество положительных корней

.

Первые двенадцать корней уравнения приведены в табл.4.1. Собственными функциями, соответствующими собственным значениям, будут функции

_.

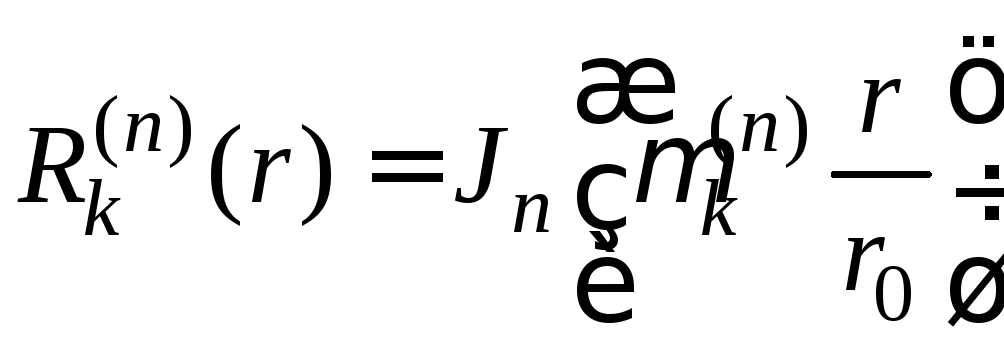Функции в пространстве ортогональны с весом . Наконец, собственные функции краевой задачи на собственные значения для уравнения Лапласа в круге представим в виде

.
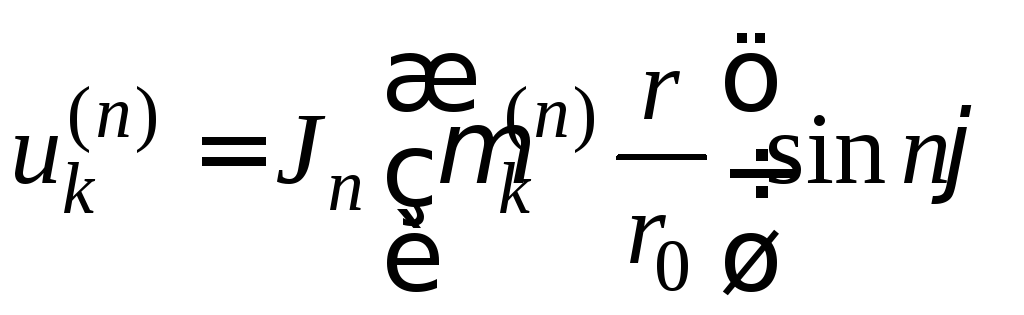