4.2. Метод разделения переменных (метод Фурье)

4.2.1. Ортогональные системы

Пусть в линейном пространстве введено скалярное произведение векторов и , определяемое свойствами:

1.  ,

2. ,

3. ,

4.  причём только при .

Число, равное , называется нормой элемента и обозначается . Последовательность векторов называется фундаментальной, если для всех существует такое , что для любых выполняется условие . Пространство называется полным, если любая фундаментальная последовательность имеет предел . Полное линейное пространство со скалярным произведением называется пространством Гильберта и символически обозначается .

Система функций , заданных в области , для которых , называется пространством со скалярным произведением

, ,

если из условия следует, что .

Система функций , заданных в области , называется ортогональной в , если

1. 

2. ,.

Система функций , заданных в области , называется ортогональной в с весом , если

1. 

2.  .

Если функция , то существуют числа

называемые коэффициентами Фурье функции по системе функций , а ряд

~

называется ортогональным разложением или рядом Фурье функции по системе функций

4.2.2. Функции Бесселя

Функциями Бесселя (цилиндрическими функциями Бесселя) называются решения дифференциального уравнения

, (16)

называемого уравнением Бесселя. Уравнение (16) является линейным уравнением второго порядка и поэтому имеет два независимых решения, в качестве которых чаще всего используются функции

, , , .

Здесь , − функции Бесселя и Неймана, , − функции Ханкеля первого и второго рода. Эти функции при определяются выражениями

,

,

,

.

Следующие рекуррентные формулы справедливы для любой цилиндрической функции :

,

,

.

Если − положительные корни уравнения

, (17)

то при функции Бесселя в пространстве ортогональны с весом , то есть

.

.

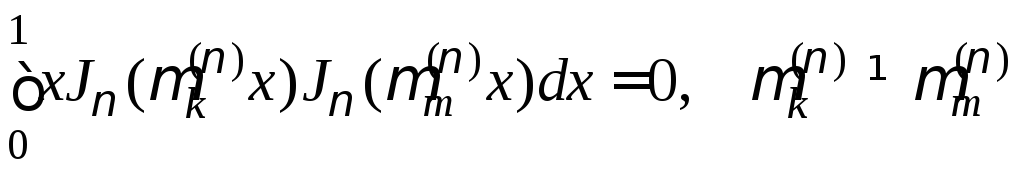Положительные корни уравнения (17) можно пронумеровать и расположить в порядке возрастания

< < <…

Для примера первые двенадцать корней уравнения приведены в таблице.

1	2,4048	5	14,9309	9	27,4935
2	5,5201	6	18,0711	10	30,6346
3	8,6537	7	21,2116	11	33,7758
4	11,7915	8	24,3525	12	36,9171

4.2.3. Модифицированные функции Бесселя

Модифицированными функциями Бесселя (модифицированными цилиндрическими функциями Бесселя) называются решения дифференциального уравнения

,

то есть функции

, .

Здесь − модифицированная функция Бесселя, – функция Макдональда. Модифицированные функции Бесселя связаны с функциями Бесселя соотношениями

,

,

.

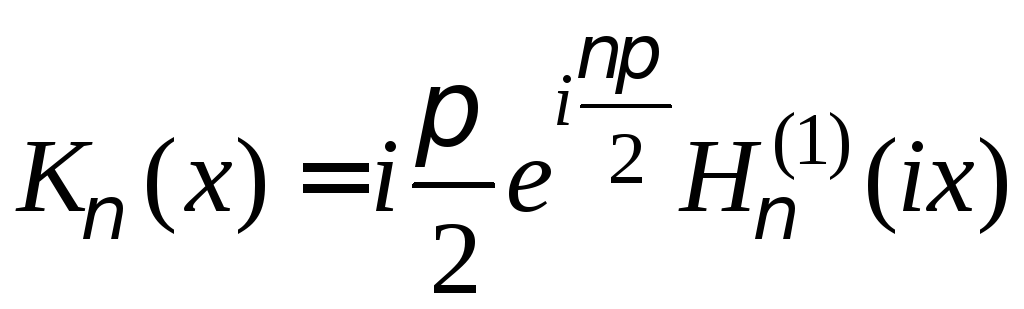Модифицированные функции Бесселя называют также функциями Бесселя мнимого аргумента. Эти функции определяются выражениями

,

.

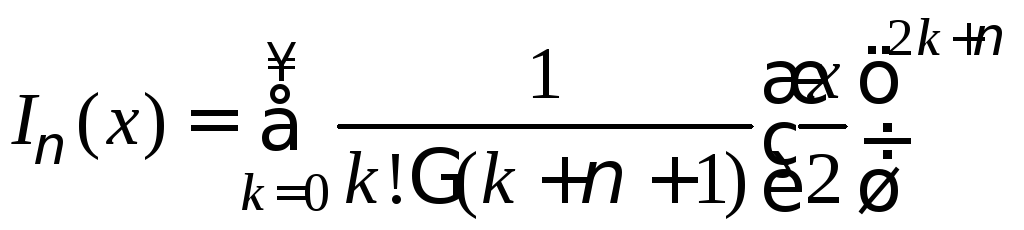Рекуррентные формулы для модифицированных функций Бесселя:

,

,

.

4.2.4. Сферические функции Бесселя

Сферическими функциями Бесселя называются решения дифференциального уравнения

. (18)

Уравнение (18) является уравнением второго порядка и поэтому имеет два независимых решения, в качестве которых чаще всего используются функции

, , , .

Здесь , − сферические функции Бесселя и Неймана, , − сферические функции Ханкеля первого и второго рода. Эти функции при определяются выражениями:

,

,

,

.

Сферические функции Бесселя связаны с цилиндрическими функциями Бесселясоотношениями

.

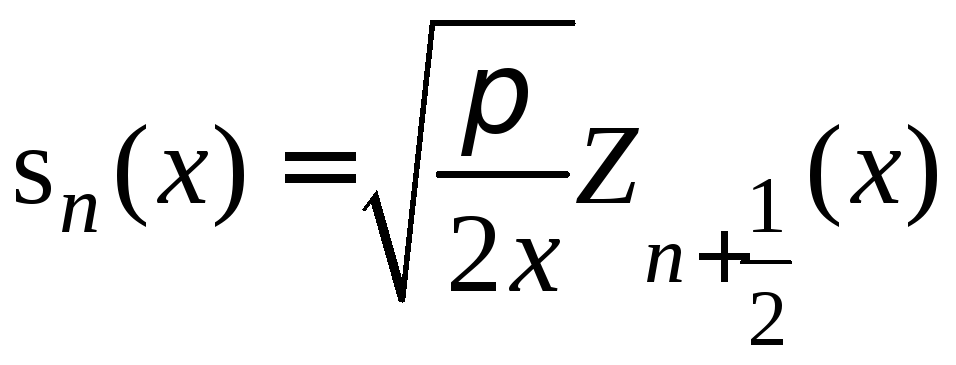Для сферических функций Бесселя справедливы следующие формулы:

–,

.

В случае целого индекса сферические функции Бесселя можно выразить через элементарные функции:

, j, . . .

, , . . .

, , . . .

, , . . .

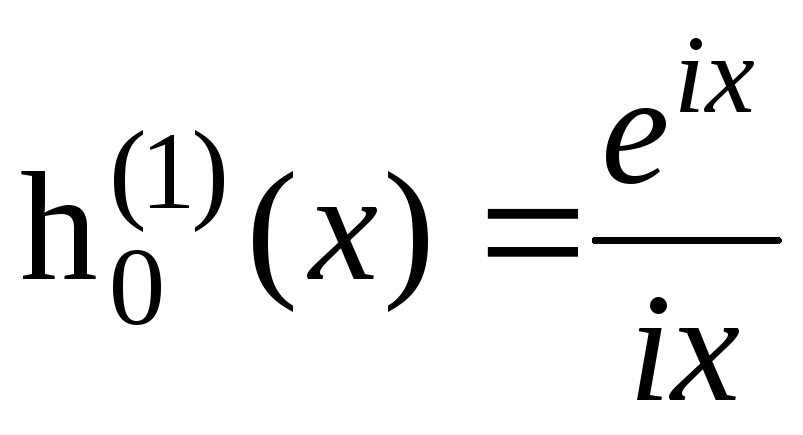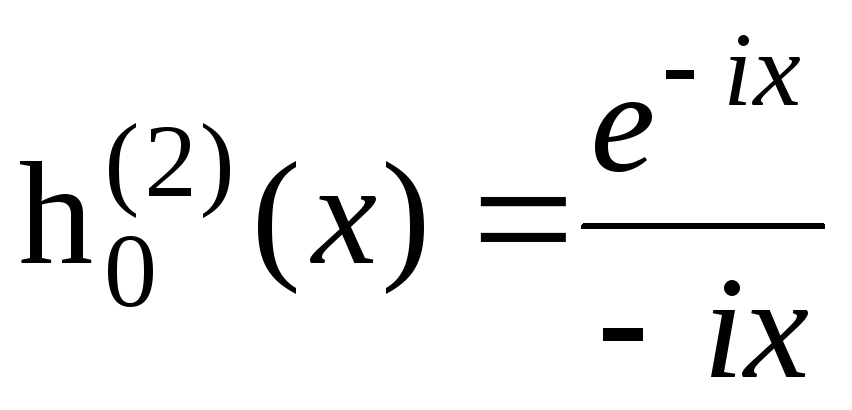Если − положительные корни уравнения

, (19)

то при функции Бесселя в пространстве ортогональны с весом , то есть

.

Положительные корни уравнения (19) можно пронумеровать и расположить в порядке возрастания

< < <…

Для примера первые двенадцать корней уравнения приведены в следующей таблице.

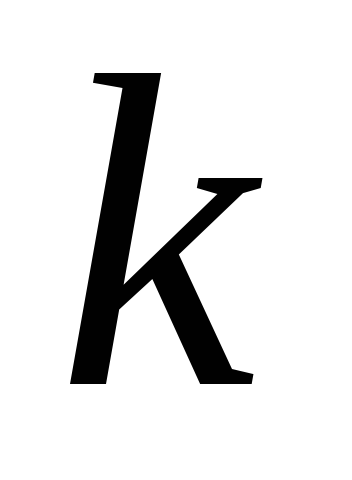
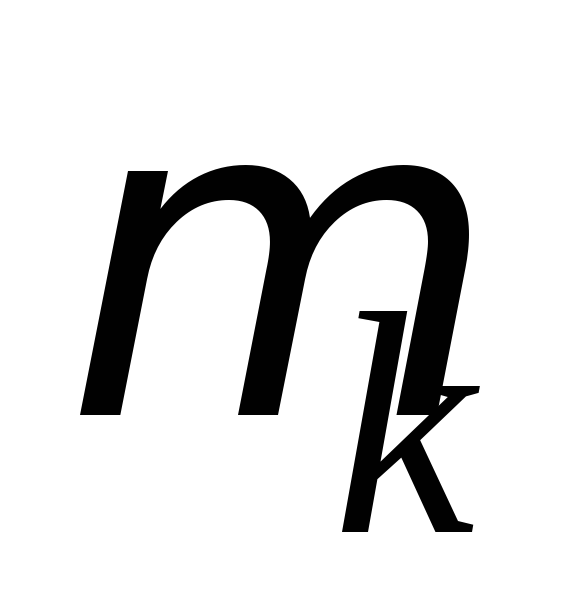
1	3,1416	5	1,708	9	28,2743
2	6,2832	6	18,8468	10	31,4159
3	9,4248	7	21,9911	11	34,5575
4	12,5664	8	25,1327	12	37,6991