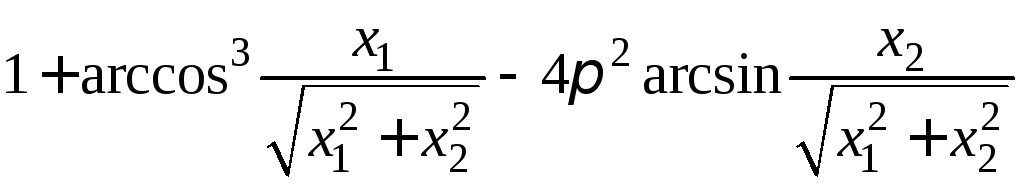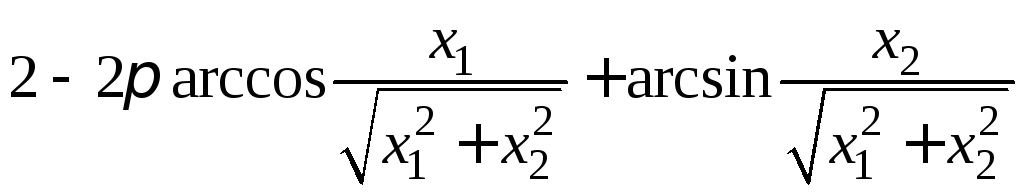- •II. Уравнения математической физики
- •1. Определение и классификация дифференциальных уравнений с частными производными
- •2. Характеристические поверхности (характеристики) квазилинейного уравнения второго порядка. Приведение квазилинейного уравнения второго порядка к каноническому виду
- •Пример 3. Приведите к каноническому виду уравнения (задание 3):
- •Пример 4. Упростите уравнения:
- •Пример 5. Найдите общее решение уравнения (задание 4)
- •3. Основные уравнения с частными производными. Задачи для уравнений с частными производными
- •4. Методы решения задач для уравнений с частными производными
- •4.1. Метод характеристик
- •4.1.1. Метод Даламбера
- •Пример 6. Найдите решение задачи Коши для однородного волнового уравнения на прямой
- •4.1.2. Фазовая плоскость
- •Вариант первый
- •Решение задачи находится по формуле Даламбера
- •Вариант второй
- •4.2. Метод разделения переменных (метод Фурье)
- •4.2.1. Ортогональные системы
- •4.2.2. Функции Бесселя
- •4.2.3. Модифицированные функции Бесселя
- •4.2.4. Сферические функции Бесселя
- •4.2.5. Шаровые и сферические функции
- •4.2.6. Схема метода Фурье
- •Пример 10. Найдите решения задачи Штурма - Лиувилля (задание 8)
- •Пример 11. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в круге
- •Пример 12. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в прямоугольнике (задание 9)
- •Пример 13. Найдите решение краевой задачи для уравнения Лапласа в круге (задание 11)
- •Пример 14. Найдите решение краевой задачи для уравнения Лапласа в прямоугольнике (задание 10)
- •Вариант первый
- •Вариант второй
- •Вариант третий
- •Пример 15. Найдите решение краевой задачи для уравнения Лапласа в шаре (задание 12)
- •Вариант третий
- •Пример 16. Найдите решение краевой задачи для уравнения Лапласа в цилиндре (задание 13)
- •Пример 17. Найдите решение краевой задачи для уравнения Пуассона в кольце (задание 14)
- •Пример 18. Найдите решение краевой задачи для уравнения Гельмгольца в круге (задание 15)
- •Имеем краевую задачу третьего рода
- •Пример 19. Найдите решение краевой задачи для уравнения Гельмгольца в шаре (задание 16)
- •Пример 21. Найдите решение смешанной задачи для однородного волнового уравнения в интервале (см. Задание17)
- •Пример 22. Найдите решение смешанной задачи для однородного волнового уравнения в прямоугольнике (задание 18)
Пример 13. Найдите решение краевой задачи для уравнения Лапласа в круге (задание 11)
![]()
 .
.
|
№ |
|
|
|
|
|
1 |
2 |
1 |
0 |
2+ |
|
2 |
3 |
0 |
1 |
|
|
3 |
1 |
2 |
1 |
|
Решение.
Уравнение
Лапласа и граничное условие запишем в
полярных координатах (![]() :
:
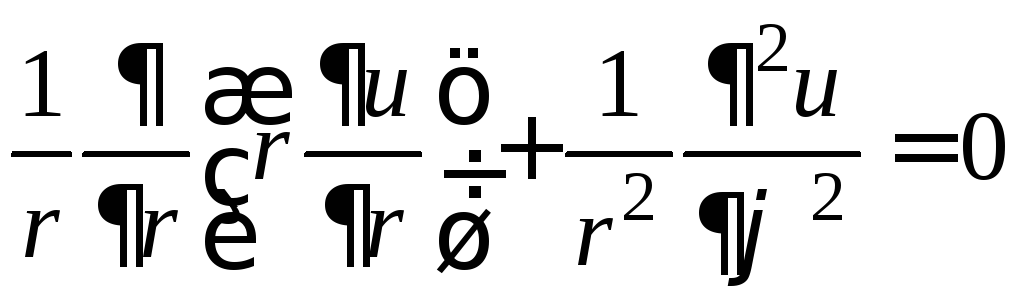 .
(1)
.
(1)
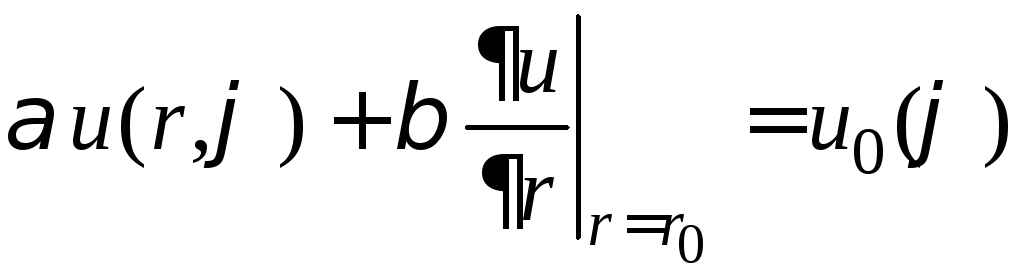 .
.
Решение ищем в виде
![]() .
(2)
.
(2)
После подстановки (2) в (1) получаем два обыкновенных дифференциальных уравнения
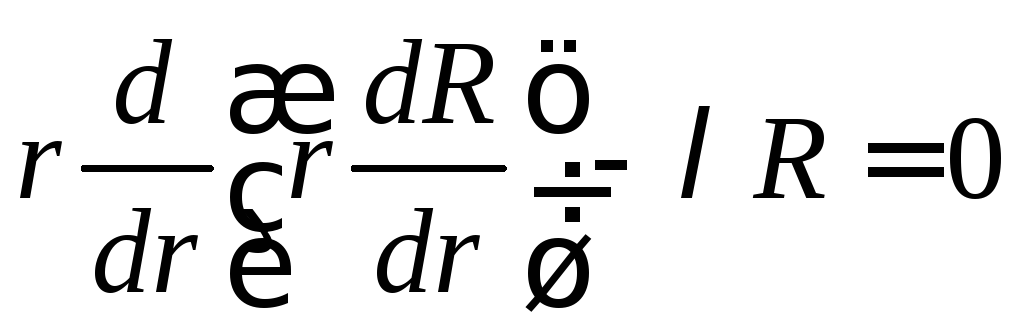 ,
(3)
,
(3)
![]() .
(4)
.
(4)
Решение
должно быть непрерывным. Это значит,
что
![]() .
Поэтому и
.
Поэтому и![]() .
Исходя из этого условия и из (4), находим
.
Исходя из этого условия и из (4), находим![]() (k
– целое
число) и
(k
– целое
число) и
![]() .
.
Уравнение
(3) есть уравнение Эйлера. Его решение
ищем в виде
![]() .
Тогда с помощью (3) получаем
.
Тогда с помощью (3) получаем![]() ,
,![]() (k
> 0) и, таким
образом,
(k
> 0) и, таким
образом,
![]() .
Еслиk
= 0
.
Еслиk
= 0
![]() ,
то из (3) находим
,
то из (3) находим![]() .
Так как решение должно быть конечным,
то необходимо положить
.
Так как решение должно быть конечным,
то необходимо положить![]() ,
иначе
,
иначе![]() и
и![]() при
при![]() .
Решение задачи (1) представим в виде ряда
Фурье
.
Решение задачи (1) представим в виде ряда
Фурье
![]() ,
(5)
,
(5)
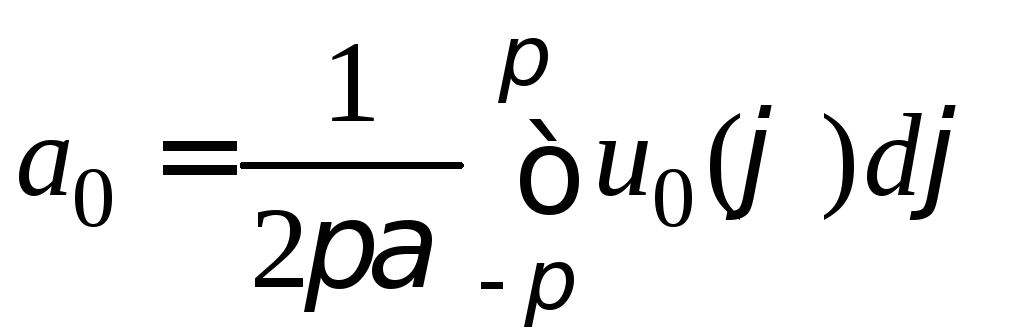 ,
,
![]() (6)
(6)
![]() .
.
Если
функция
![]()
![]() периодическая
с периодом
периодическая
с периодом
![]() имеет непрерывную первую производную
и кусочно-непрерывную вторую производную
и
имеет непрерывную первую производную
и кусочно-непрерывную вторую производную
и
![]()
![]() ,
то ряд (5) после
двукратного дифференцирования по
переменным
,
то ряд (5) после
двукратного дифференцирования по
переменным
![]() и
и![]() будетсходиться
при
будетсходиться
при
![]() равномерно. Поэтомувыражение
(5) будет являться решением задачи (1).
равномерно. Поэтомувыражение
(5) будет являться решением задачи (1).
Рассмотрим теперь различные варианты предложенной задачи.
Вариант первый
|
№ |
|
|
|
|
|
1 |
2 |
1 |
0 |
2+ |
Это краевая задача первого рода (задача Дирихле) для уравнения Лапласа в круге
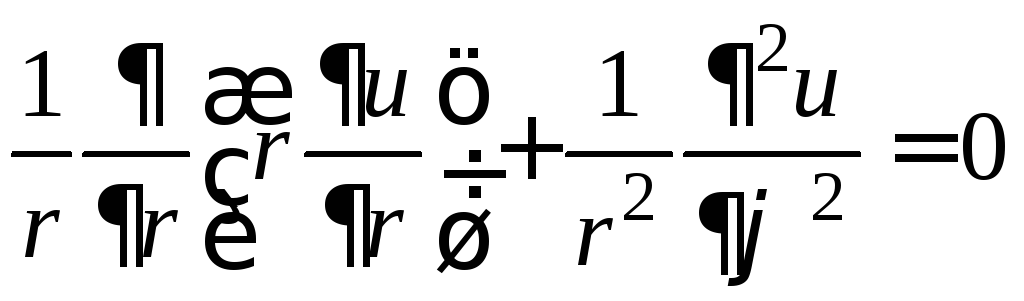 .
.
![]()
![]() .
.
По формулам (6) находим
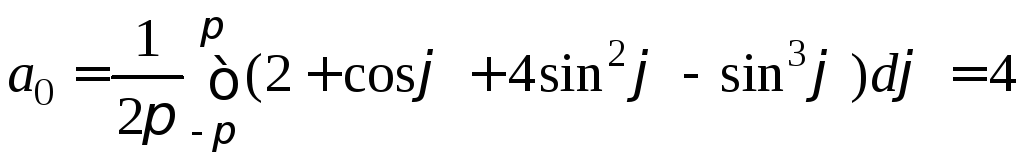 ,
,

![]() ,
,

![]() .
.
Подставляем значения коэффициентов в формулу (5) и получаем искомое решение
![]() .
.
Вариант второй
|
№ |
|
|
|
|
|
2 |
3 |
0 |
1 |
|
Это краевая задача второго рода (задача Неймана) для уравнения Лапласа в круге
 .
.

![]() ,
,
![]() ,
,
где
![]()

По формулам (6) находим
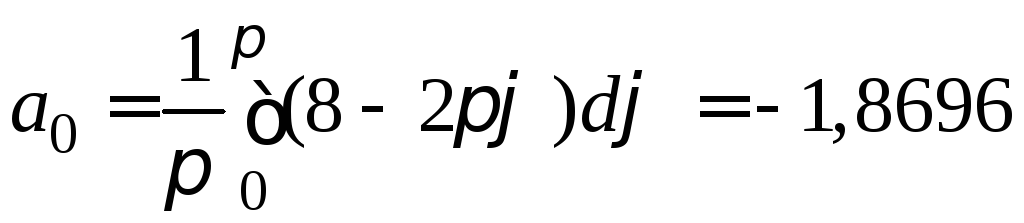 ,
,
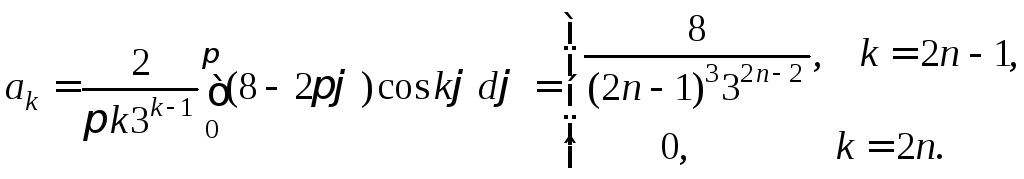
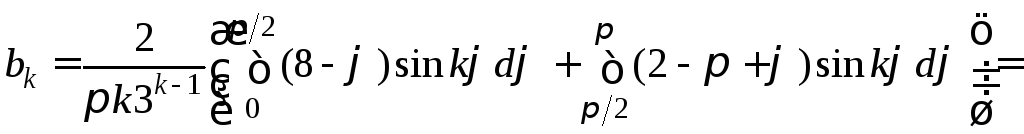
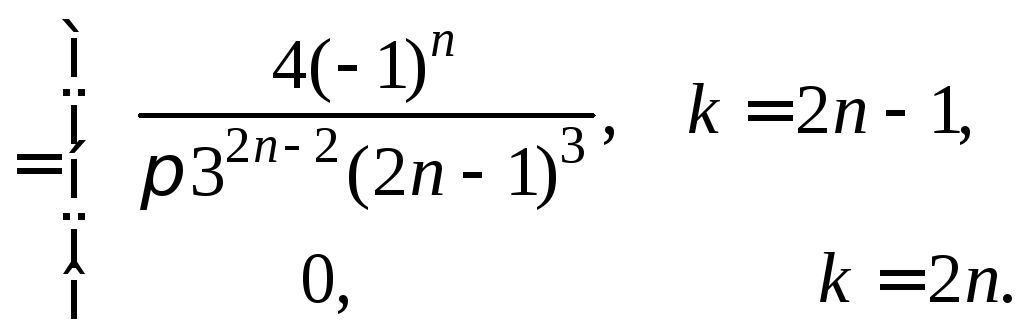
При
вычислении коэффициентов
![]() использовалось свойство интеграла от
периодической функции
использовалось свойство интеграла от
периодической функции
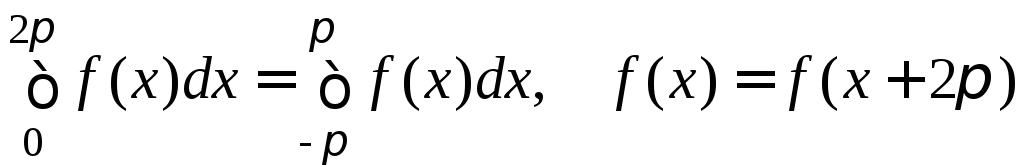 ,
,
а также свойство интеграла от чётной или нечётной функций
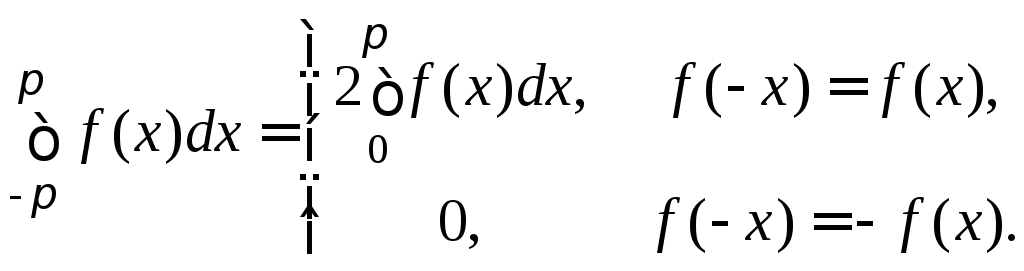
Подставляем найденные коэффициенты в формулу (5) и получаем искомое решение
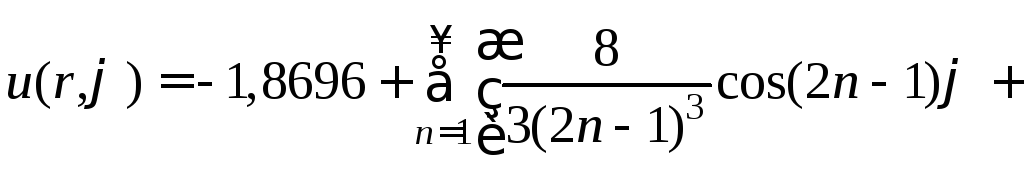

![]()
![]()
![]()
![]()
![]() …
…
Вариант третий
|
№ |
|
|
|
|
|
3 |
1 |
2 |
1 |
|
Это краевая задача третьего рода для уравнения Лапласа в круге
 ,
,
![]()
![]() ,
,
![]() ,
,
где
![]()
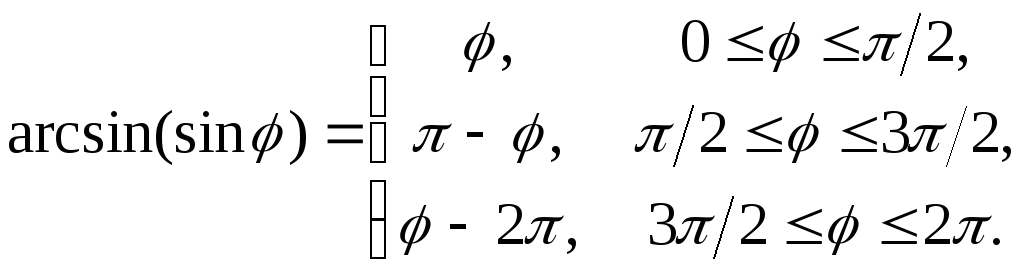
Вычисляем коэффициенты
 ,
,
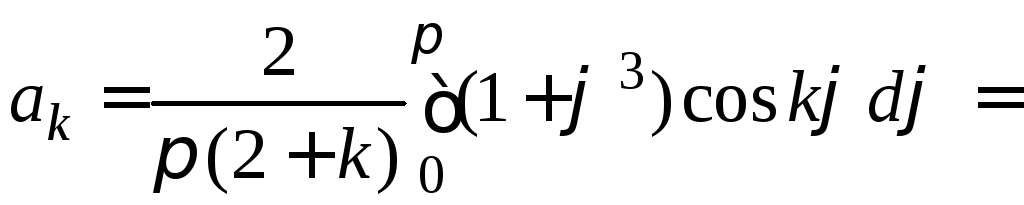
 ,
,
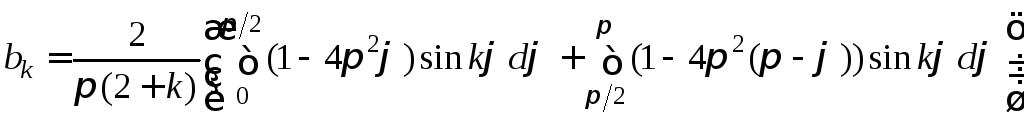 =
=
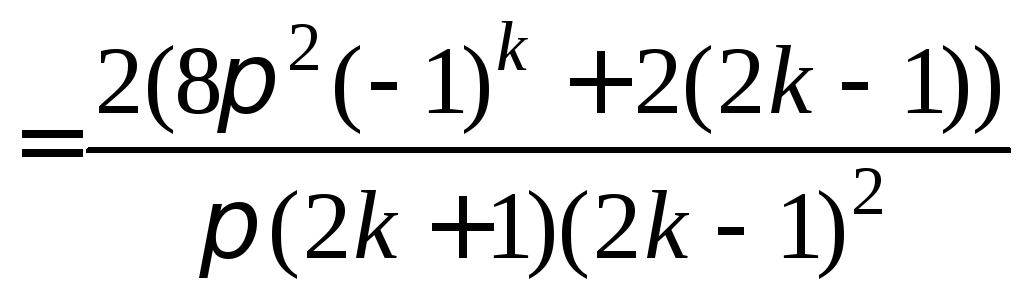 .
.
Подставляем коэффициенты в формулу (5) и получаем искомое решение

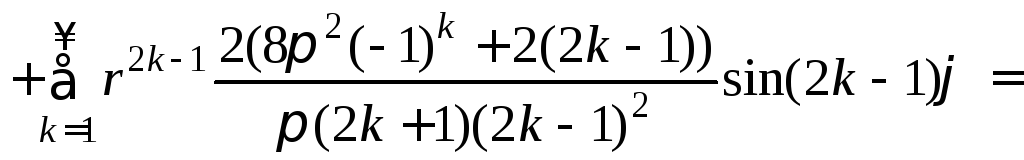
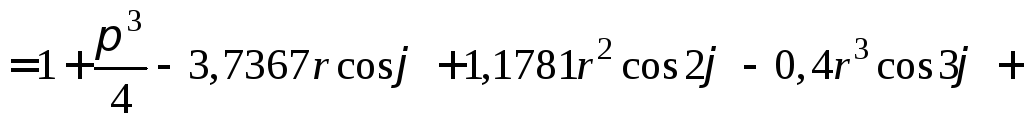
![]()
![]()
Пример 14. Найдите решение краевой задачи для уравнения Лапласа в прямоугольнике (задание 10)
![]() (1)
(1)
![]()
 (2)
(2)
![]()
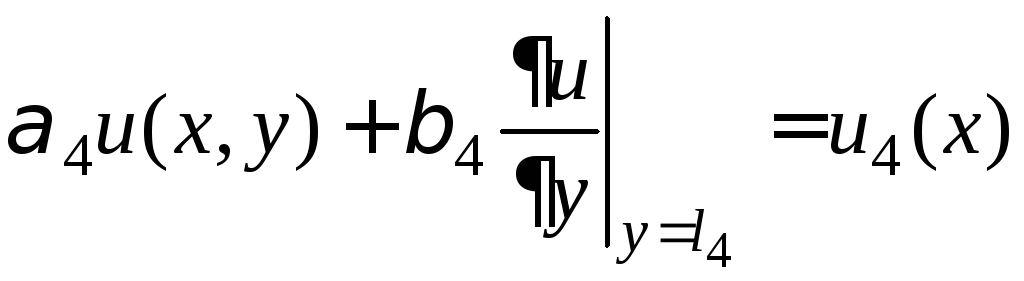 .
(3)
.
(3)
|
№ |
|
|
|
| ||||||||||
|
1 |
|
0 |
0 |
| ||||||||||
|
2 |
0 |
|
|
0 | ||||||||||
|
3 |
|
|
|
| ||||||||||
|
№ |
|
|
|
|
|
|
|
|
|
|
|
| ||
|
1 |
0 |
1 |
0 |
2 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 | ||
|
2 |
0 |
2 |
−2 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 | ||
|
3 |
−1 |
1 |
0 |
3 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 | ||
Решение задачи представим в виде
![]() ,
,
где
![]() является
решением краевой задачи
является
решением краевой задачи
![]() (4)
(4)
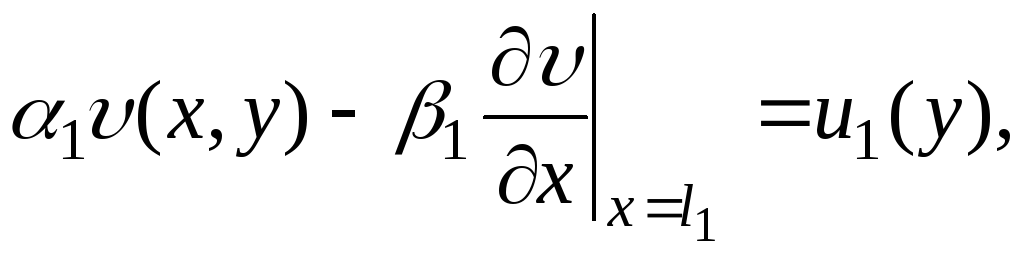
 (5)
(5)
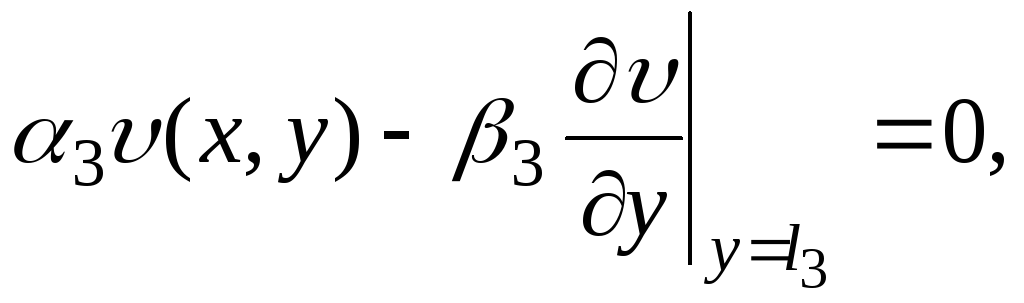
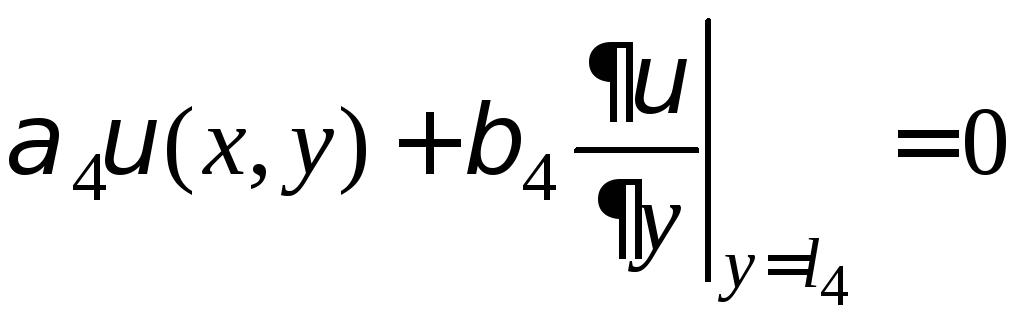 ,
(6)
,
(6)
а
![]() −
краевой задачи
−
краевой задачи
![]() (7)
(7)
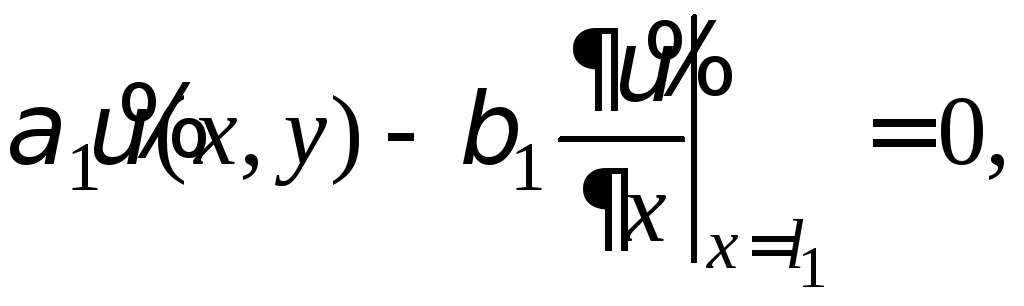
 (8)
(8)

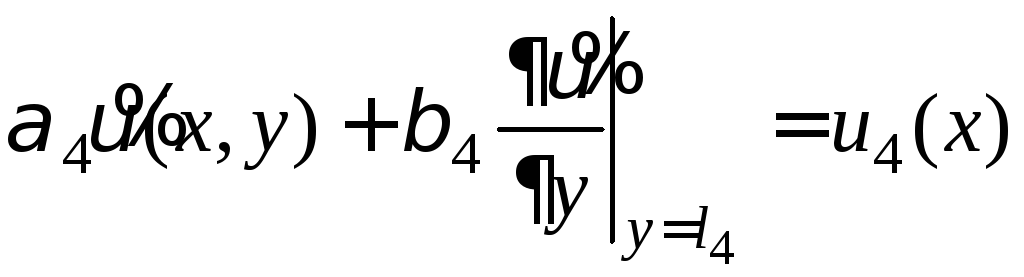 .
(9)
.
(9)
С помощью замены
![]() (10)
(10)
уравнение (4) сводится к двум обыкновенным дифференциальным уравнениям
![]() ,
(11)
,
(11)
![]() ,
,
![]()
![]() .
(12)
.
(12)
Задача (12) − задача Штурма - Лиувилля (см. пример 10) с характеристическим уравнением
![]() (13)
(13)
и собственными функциями
![]()
или
![]() ,
,
где
![]() − корни уравнения (13). Уравнение (11) при
− корни уравнения (13). Уравнение (11) при![]() имеет общее решение
имеет общее решение
![]() . (14)
. (14)
Решение задачи (4) – (6) представим в виде ряда
![]()
![]() . (15)
. (15)
С помощью граничных условий (5) находим коэффициенты

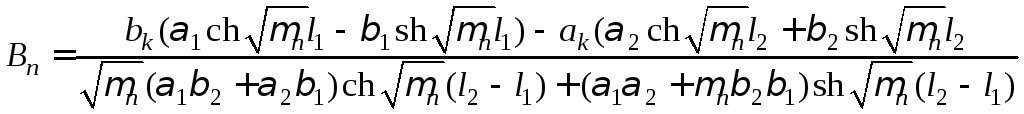 ,
,
где
 ,
(16)
,
(16)
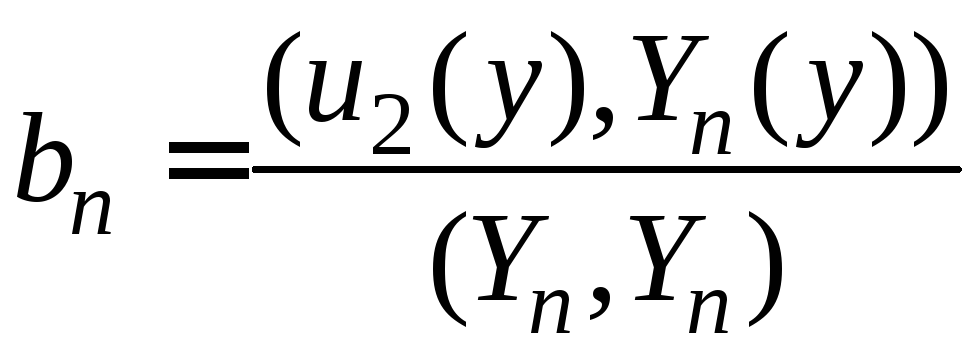 .
(17)
.
(17)
Подставляем
найденные значения постоянных
![]() и
и
![]() в (15) и после элементарных преобразований
получаем решение задачи (4) − (6)
в (15) и после элементарных преобразований
получаем решение задачи (4) − (6)
![]()
![]() ,
,
где
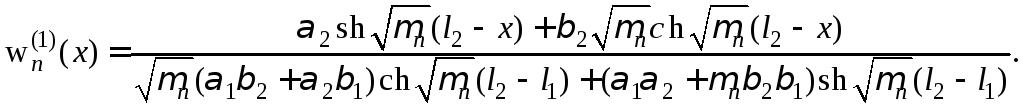 (18)
(18)
 (19)
(19)
Аналогично находим решение краевой задачи (7) − (9)
![]()
![]() ,
,
где
 (20)
(20)
 (21)
(21)
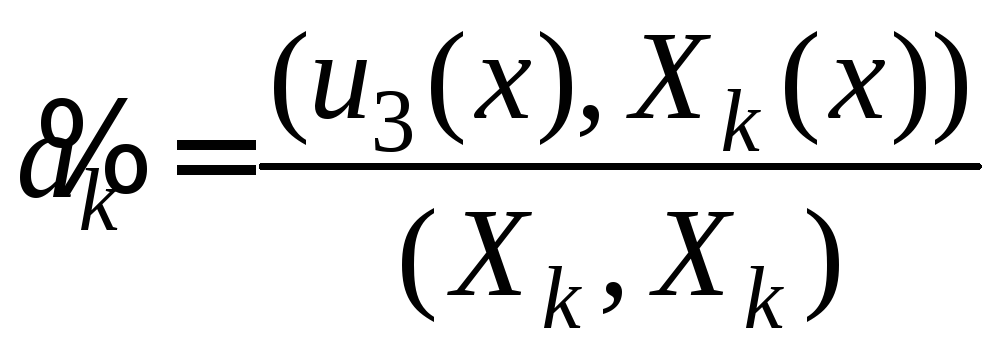 . (22)
. (22)
![]() . (23)
. (23)
Решение задачи (1) − (3) получаем в виде
![]()
![]()
![]() .
(24)
.
(24)
Рассмотрим заданные варианты задачи.