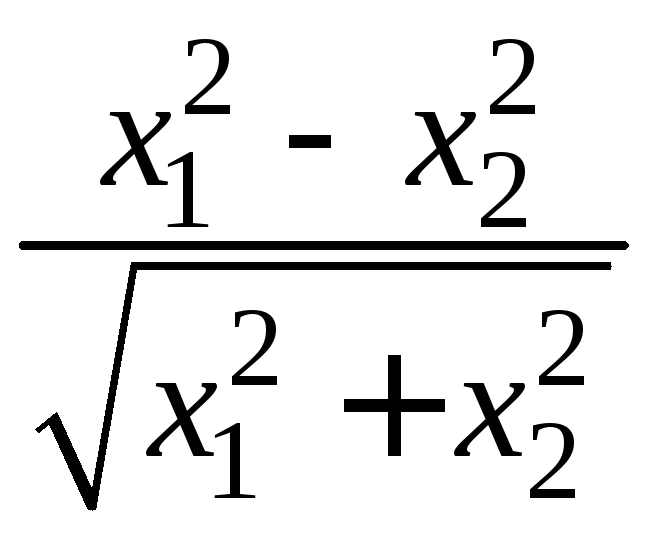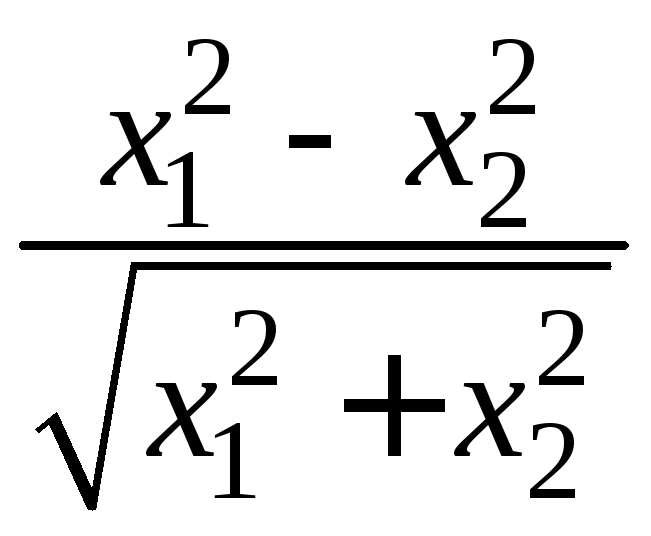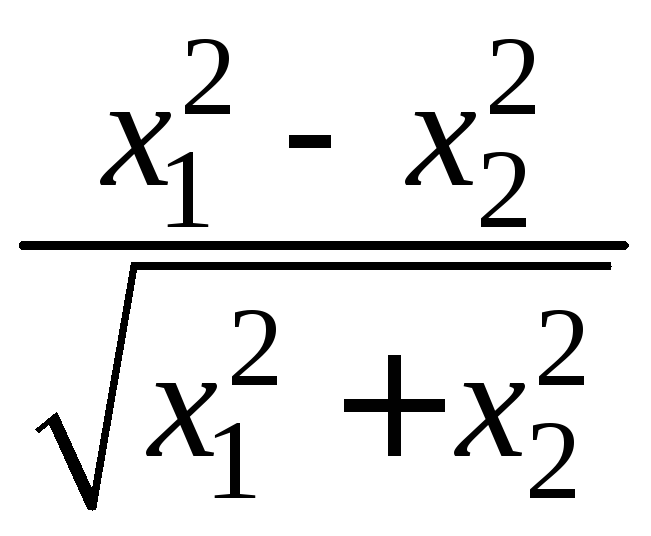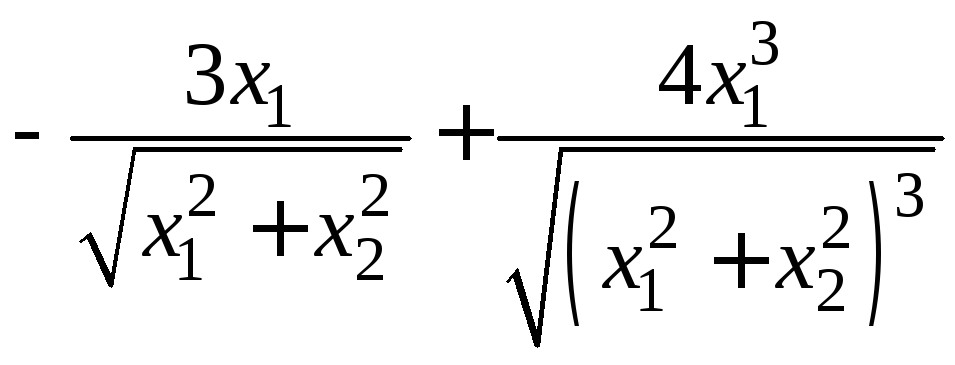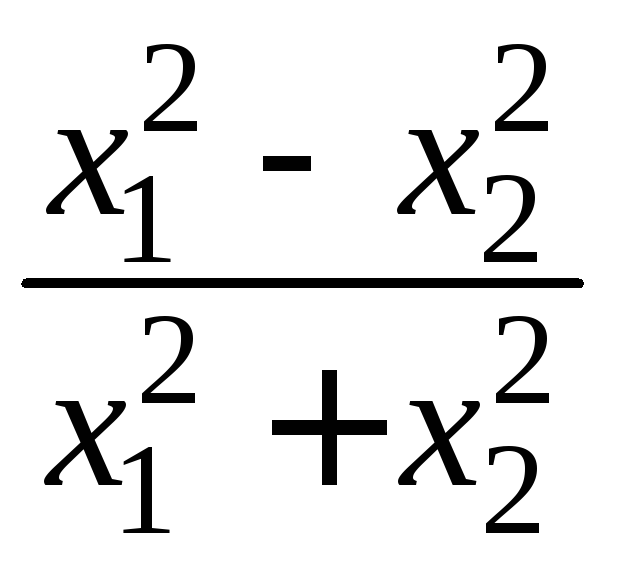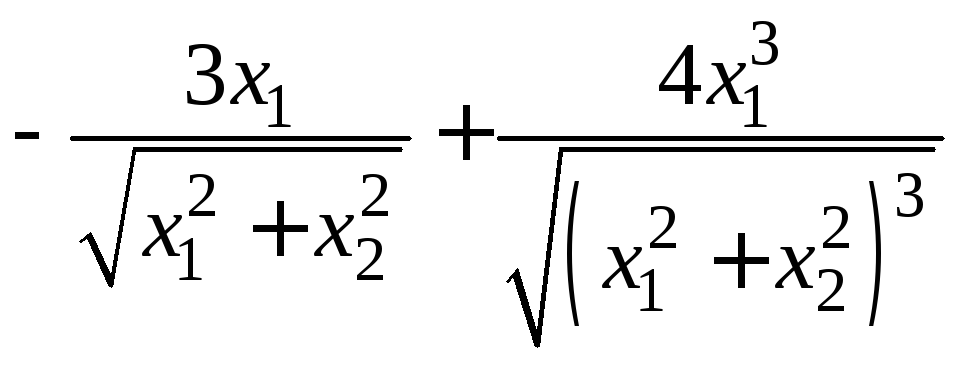- •II. Уравнения математической физики
- •1. Определение и классификация дифференциальных уравнений с частными производными
- •2. Характеристические поверхности (характеристики) квазилинейного уравнения второго порядка. Приведение квазилинейного уравнения второго порядка к каноническому виду
- •Пример 3. Приведите к каноническому виду уравнения (задание 3):
- •Пример 4. Упростите уравнения:
- •Пример 5. Найдите общее решение уравнения (задание 4)
- •3. Основные уравнения с частными производными. Задачи для уравнений с частными производными
- •4. Методы решения задач для уравнений с частными производными
- •4.1. Метод характеристик
- •4.1.1. Метод Даламбера
- •Пример 6. Найдите решение задачи Коши для однородного волнового уравнения на прямой
- •4.1.2. Фазовая плоскость
- •Вариант первый
- •Решение задачи находится по формуле Даламбера
- •Вариант второй
- •4.2. Метод разделения переменных (метод Фурье)
- •4.2.1. Ортогональные системы
- •4.2.2. Функции Бесселя
- •4.2.3. Модифицированные функции Бесселя
- •4.2.4. Сферические функции Бесселя
- •4.2.5. Шаровые и сферические функции
- •4.2.6. Схема метода Фурье
- •Пример 10. Найдите решения задачи Штурма - Лиувилля (задание 8)
- •Пример 11. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в круге
- •Пример 12. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в прямоугольнике (задание 9)
- •Пример 13. Найдите решение краевой задачи для уравнения Лапласа в круге (задание 11)
- •Пример 14. Найдите решение краевой задачи для уравнения Лапласа в прямоугольнике (задание 10)
- •Вариант первый
- •Вариант второй
- •Вариант третий
- •Пример 15. Найдите решение краевой задачи для уравнения Лапласа в шаре (задание 12)
- •Вариант третий
- •Пример 16. Найдите решение краевой задачи для уравнения Лапласа в цилиндре (задание 13)
- •Пример 17. Найдите решение краевой задачи для уравнения Пуассона в кольце (задание 14)
- •Пример 18. Найдите решение краевой задачи для уравнения Гельмгольца в круге (задание 15)
- •Имеем краевую задачу третьего рода
- •Пример 19. Найдите решение краевой задачи для уравнения Гельмгольца в шаре (задание 16)
- •Пример 21. Найдите решение смешанной задачи для однородного волнового уравнения в интервале (см. Задание17)
- •Пример 22. Найдите решение смешанной задачи для однородного волнового уравнения в прямоугольнике (задание 18)
Пример 17. Найдите решение краевой задачи для уравнения Пуассона в кольце (задание 14)
![]() ,
(1)
,
(1)
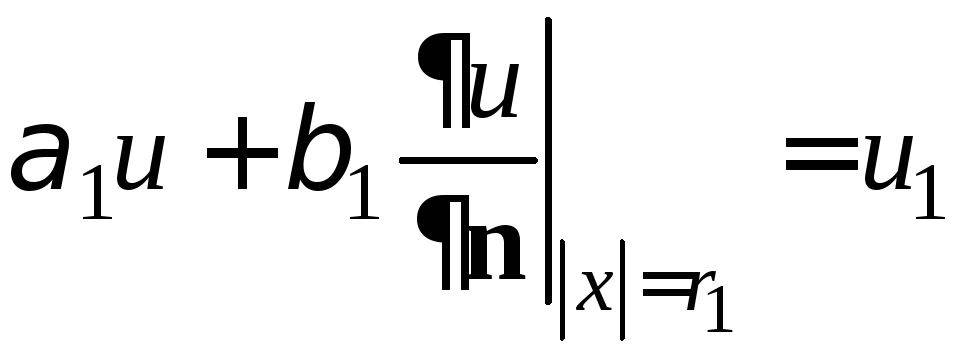 , (2)
, (2)
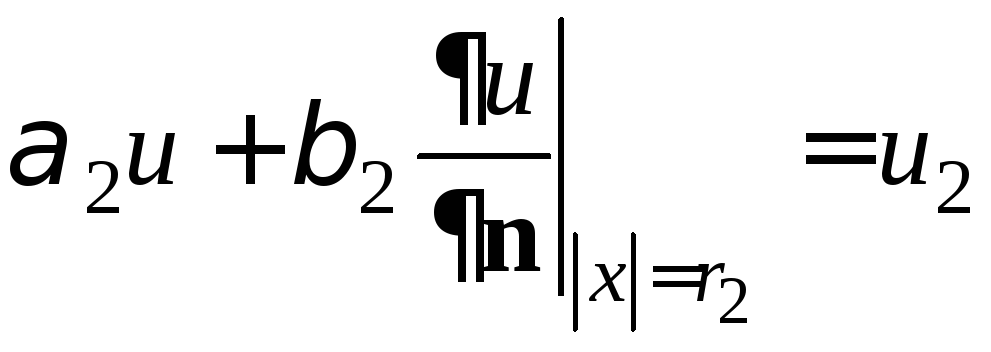 ,
(3)
,
(3)
|
№ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
Решение краевой задачи для уравнения Пуассона нужно искать в виде
![]() ,
(4)
,
(4)
где
![]() − решение краевой задачи для уравнения
Лапласа
− решение краевой задачи для уравнения
Лапласа
![]()
![]() (5)
(5)
 (6)
(6)
а
![]() − решение краевой задачи для уравнения
Пуассона
− решение краевой задачи для уравнения
Пуассона
![]()
![]() ,
(7)
,
(7)
 .
(8)
.
(8)
Рассмотрим предложенные варианты задачи.
Вариант первый
|
№ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Задача (5) − (6) в данном случае будет краевой задачей третьего рода для уравнения Лапласа
![]()
![]()
![]() ,
,
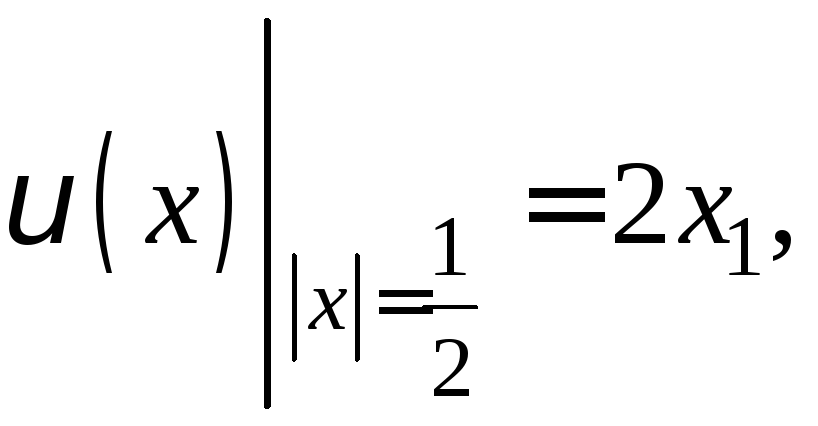
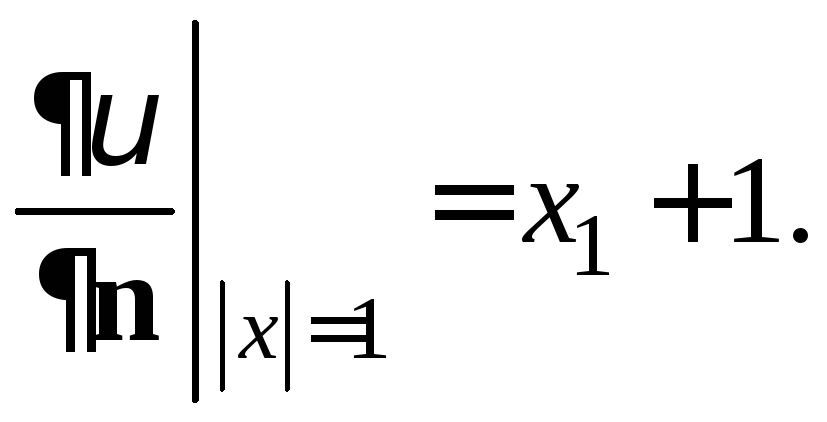
В полярных
координатах (![]()
![]() )
задача примет вид
)
задача примет вид
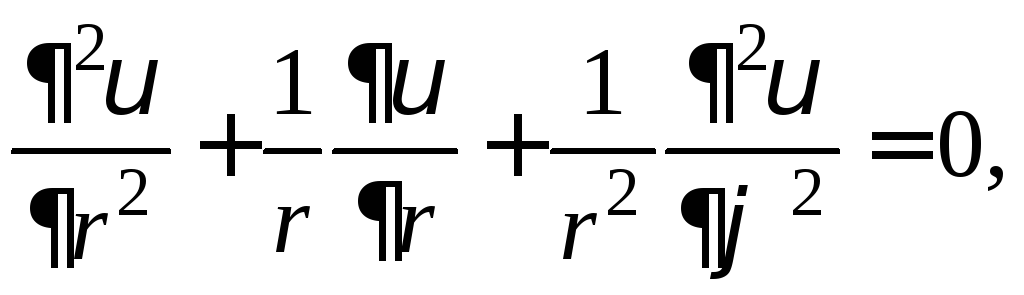
![]()
![]() (9)
(9)
 (10)
(10)
 (11)
(11)
Решение будем искать в виде
![]() (12)
(12)
Подставим выражение (12) в уравнение (9)
![]()
Умножим
обе части равенства на![]() и получим
и получим
![]()
или
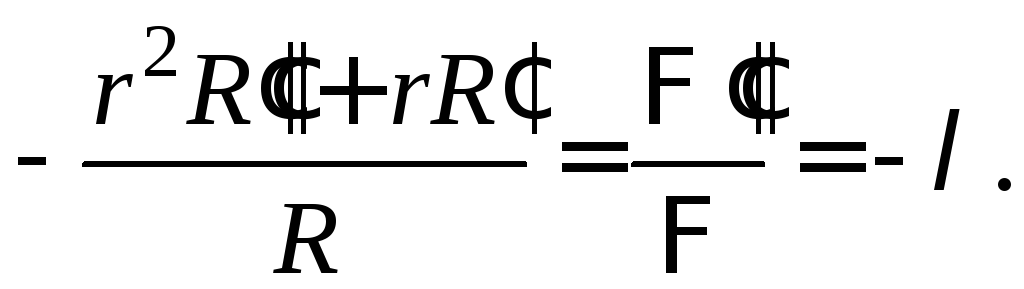
Из
последнего соотношения для нахождения
функций
![]() и
и![]() приходим к двум обыкновенным
дифференциальным уравнениям
приходим к двум обыкновенным
дифференциальным уравнениям
![]()
![]() (13)
(13)
![]() .
(14)
.
(14)
Общее решение уравнения (13) имеет вид
![]() .
.
Из
очевидного равенства
![]() следует, что
следует, что![]() .
Значит,
.
Значит,![]() и
и
![]() .
.
Уравнение (14) есть уравнение Эйлера. Его решения следует искать в виде
![]() .
(15)
.
(15)
Подставим
выражение (15) и
![]() в уравнение (14)
в уравнение (14)
![]() ,
,
откуда
![]()
или
![]() ,
,![]() .
.
Значит, решение уравнения (6) будет равно
![]()
![]()
При
![]() непосредственным интегрированием
уравнения (14) получаем
непосредственным интегрированием
уравнения (14) получаем
![]()
![]() .
.
Подставим найденные значения
![]() и
и![]() в (12)
в (12)
![]()
![]() ,
,

![]()
Наконец, решение уравнения (9) ищем в виде
 .
(16)
.
(16)
Неизвестные коэффициенты находим с помощью граничных условий
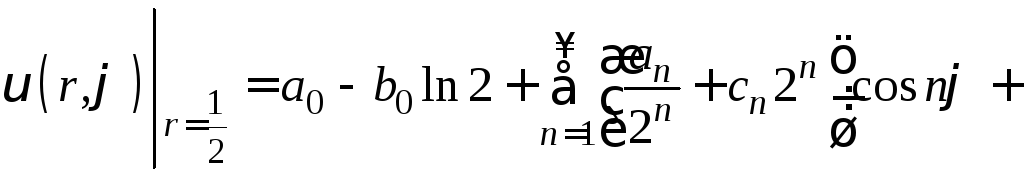
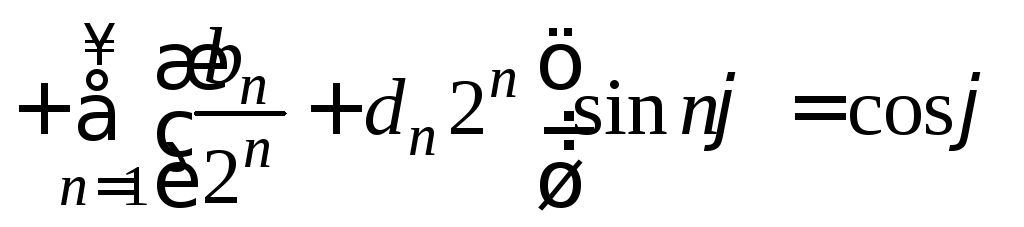 ,
(17)
,
(17)

![]() .
(18)
.
(18)
Из выражений (17) и (18) получаем систему
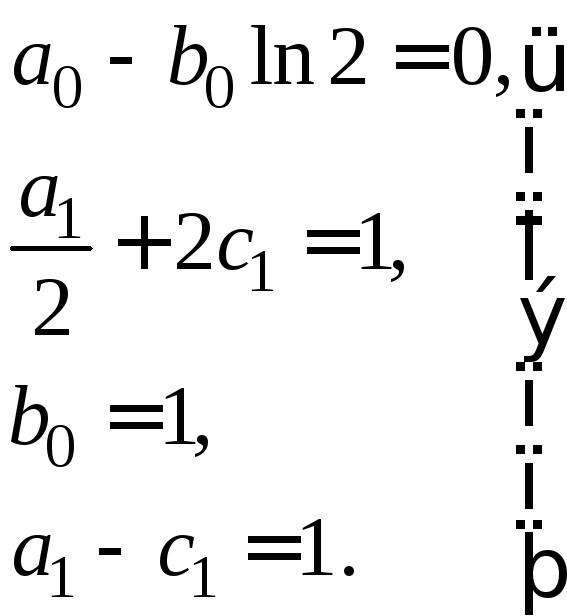 ,
,
решая
которую, находим
![]() ,
,![]() ,
,![]() ,
,![]() .
Остальные коэффициенты равны нулю.
Подставляем найденные значения
коэффициентов в выражение (16)
.
Остальные коэффициенты равны нулю.
Подставляем найденные значения
коэффициентов в выражение (16)
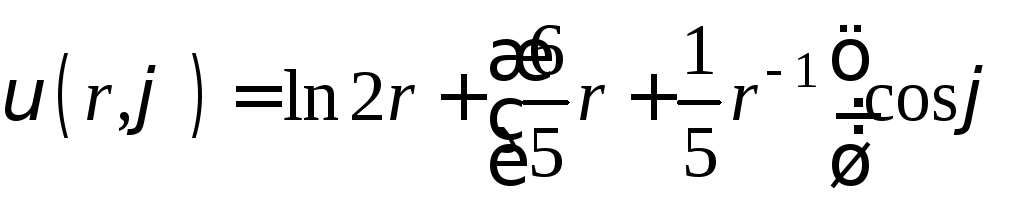 .
(19)
.
(19)
Задача (7) − (8) является краевой задачей третьего рода для уравнения Пуассона
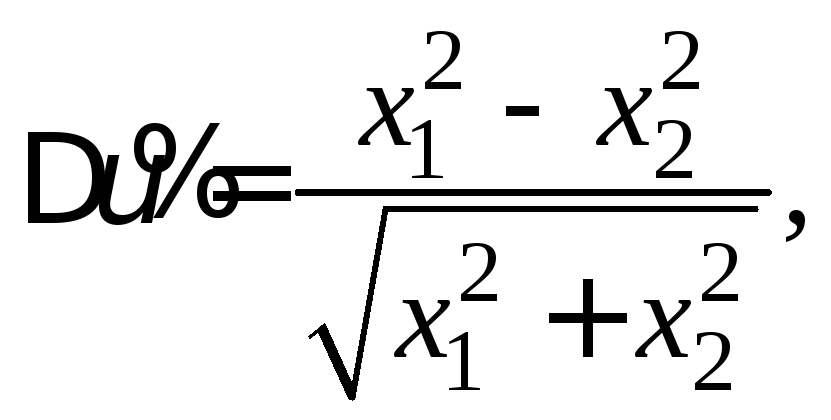
![]()
![]()
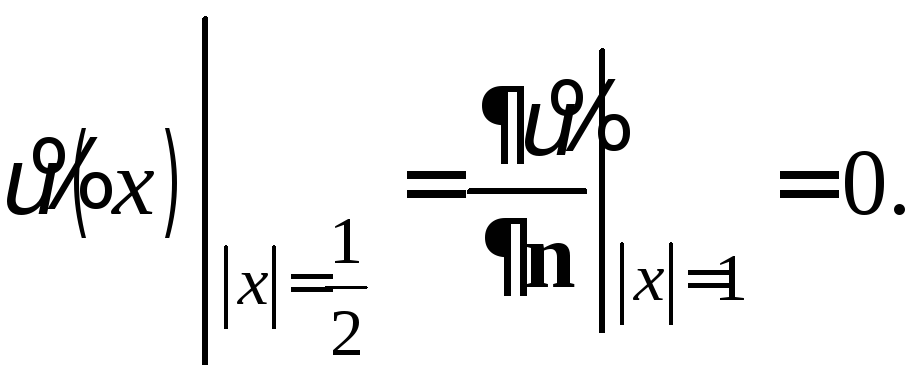
В полярных координатах задача примет вид
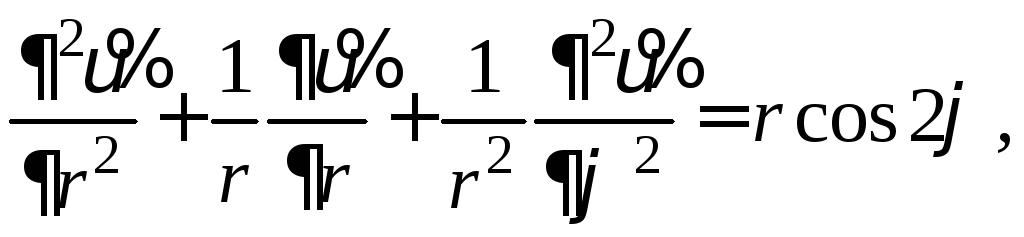
![]()
![]() (20)
(20)
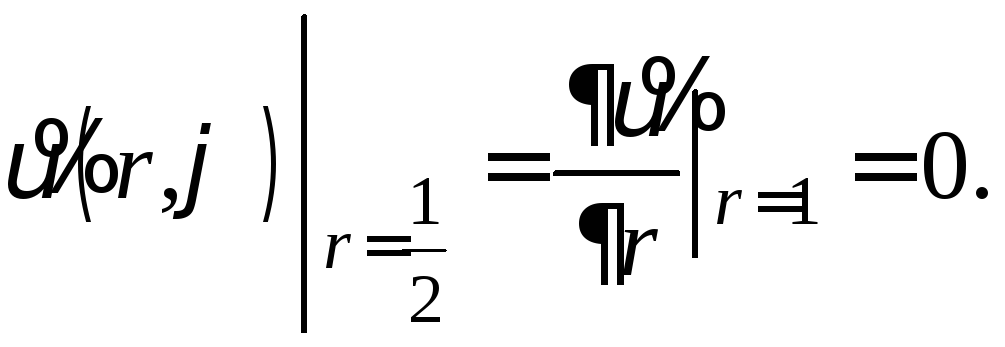 (21)
(21)
Решение будем искать в виде
![]() (22)
(22)
Подставим выражение (22) в уравнение (20)
![]() (23)
(23)
Очевидно,
![]() С учётом этого уравнение (23) примет вид
С учётом этого уравнение (23) примет вид
![]() .
(24)
.
(24)
Решение этого уравнения представим в виде
![]() (25)
(25)
где
![]() − общее решение однородного уравнения
− общее решение однородного уравнения
![]() (26)
(26)
а
![]() − какое-либо частное решение неоднородного
уравнения
− какое-либо частное решение неоднородного
уравнения
![]() (27)
(27)
Уравнение (22) есть уравнение Эйлера. Его решение имеет вид
![]()
С учётом этого получаем
![]()
откуда
находим
![]() .
Итак, общее решение уравнения (26) будет
иметь вид
.
Итак, общее решение уравнения (26) будет
иметь вид
![]()
Какое-либо частное решение уравнения (27) можно найти с помощью метода вариации постоянных. Приводим окончательный результат
![]()
Подставляем
найденные значения
![]() и
и![]() в формулу (25)
в формулу (25)
![]()
Возвращаясь к выражению (22), имеем
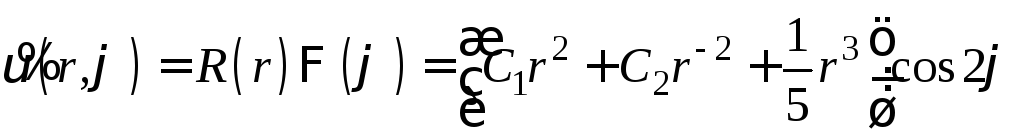 .
.
Значения постоянных
![]() и
и![]() найдём с помощью граничных условий (21)
найдём с помощью граничных условий (21)
![]()
![]()
откуда имеем
![]()
![]() и
и
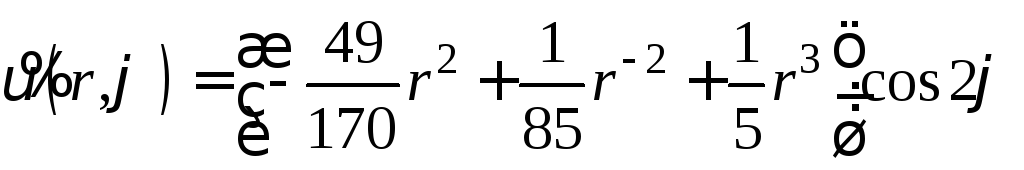 .
(28)
.
(28)
Искомое решение задачи (1) − (3) получим после подстановки выражений (19) и (28) в формулу (4)
 .
.
Вариант второй
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача (5) − (6) (задача Дирихле для уравнения Лапласа) в полярных координатах примет вид
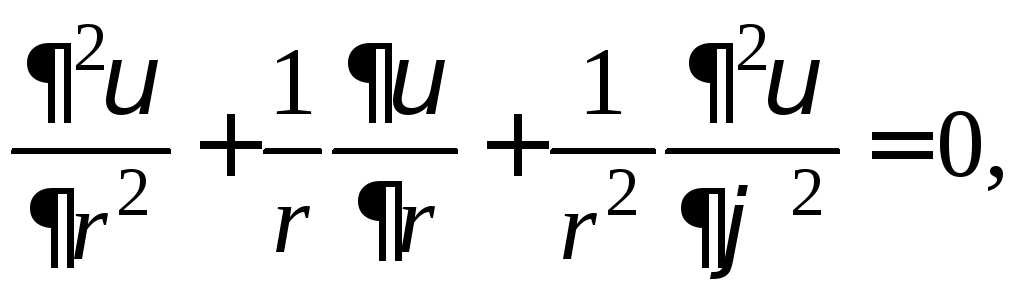
![]()
![]() (29)
(29)
![]() ,
,![]() .
.
Решение будем искать по формуле (12). Повторяя процедуру вычислений, выполненных в предыдущем варианте, находим общее решение уравнения (29), совпадающее с выражением (16). Граничные условия для решения (16)


![]()
приводят к системе
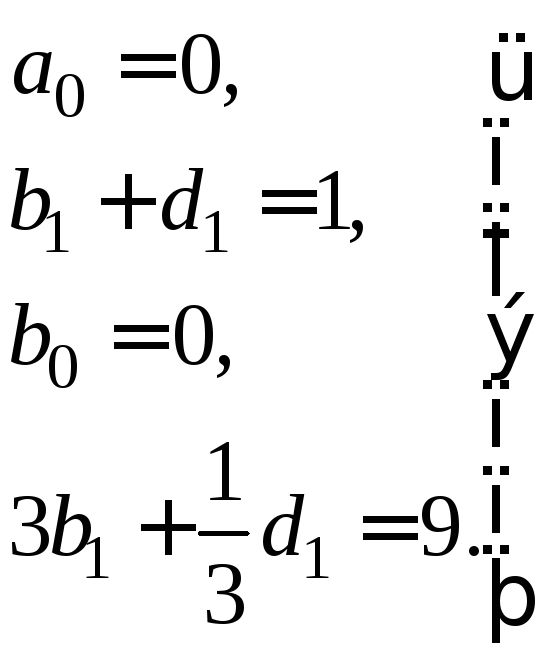 ,
,
решая которую, находим![]()
![]()
![]()
![]() Остальные
Остальные
коэффициенты равны нулю. Подставляем найденные значения коэффициентов в выражение (16)
 .
(30)
.
(30)
Задача (7) − (8) является задачей Дирихле для уравнения Пуассона. В полярных координатах она примет вид
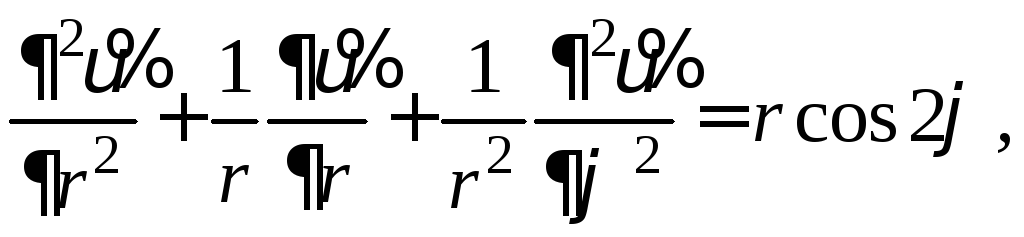
![]()
![]()
![]()
Дальнейшие вычисления такие же, как и при решении задачи (20) − (21). Поэтому приводим окончательный результат
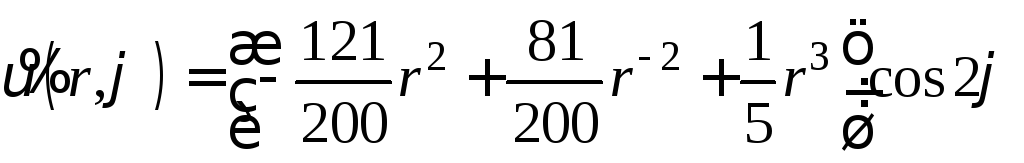 .
(31)
.
(31)
Решение задачи (1) − (3) получим после подстановки выражений (30) и (31) в формулу (4)
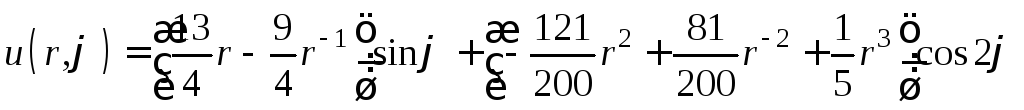 .
.
Вариант третий
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача (5) − (6) (задача Неймана для уравнения Лапласа) в полярных координатах примет вид
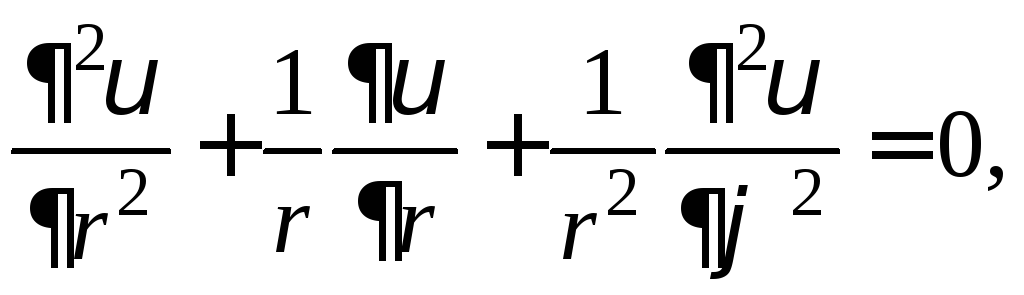
![]()
![]() (32)
(32)
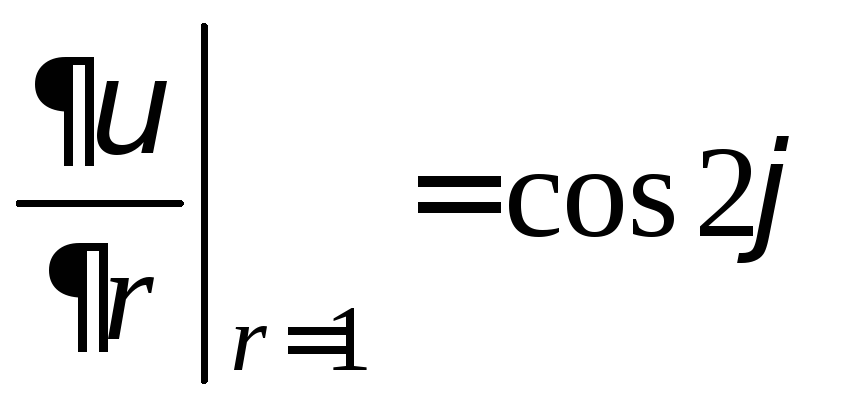 ,
,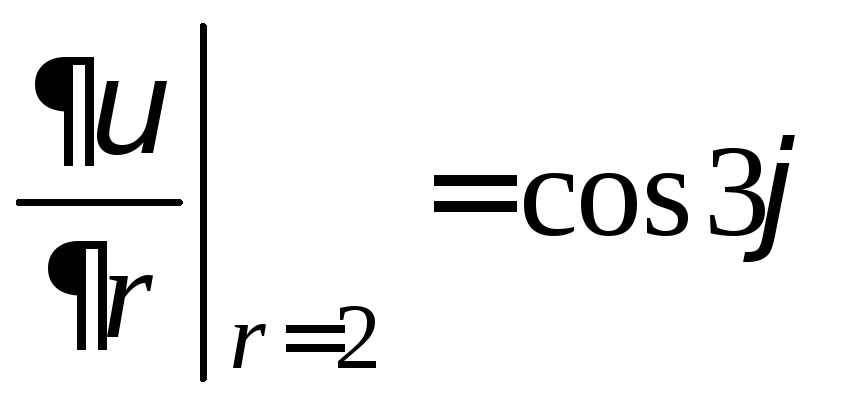 .
.
Находим общее решение уравнения (32), совпадающее с выражением (16) (см. вариант №1). Подставляем найденное решение в граничные условия

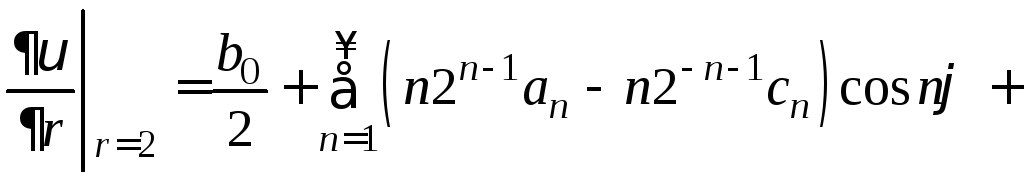
![]() .
.
и составляем систему
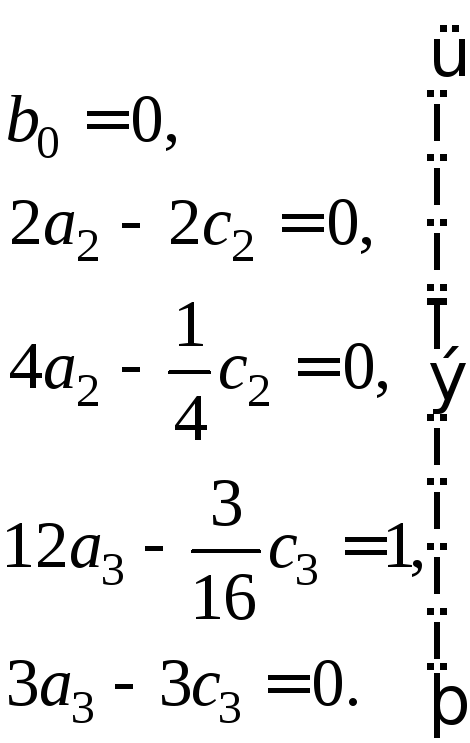 ,
,
решая которую, находим
![]()
![]()
![]()
![]()
![]()
Остальные коэффициенты равны нулю. Подставляем найденные значения коэффициентов в выражение (16)
 .
(33)
.
(33)
Задача (7) − (8) является задачей Неймана для уравнения Пуассона. В полярных координатах она примет вид

![]()
![]()
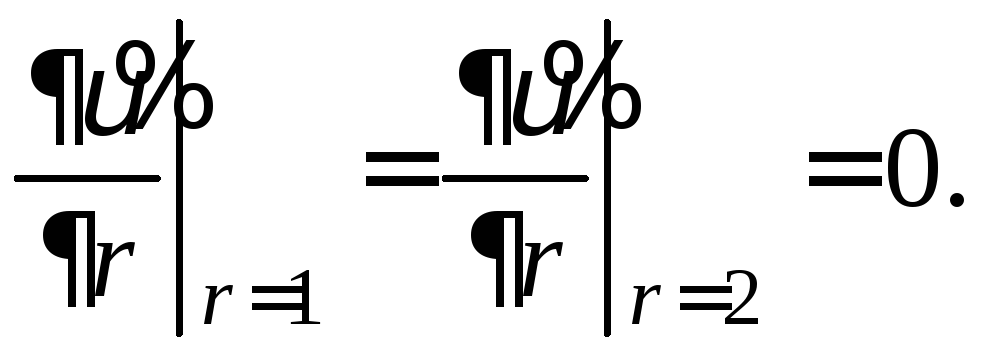
Дальнейшие вычисления такие же, как и при решении задачи (20) − (21). Поэтому приводим окончательный результат
 .
(34)
.
(34)
Решение задачи (1) − (3) получим после подстановки выражений (33) и (34) в формулу (4)
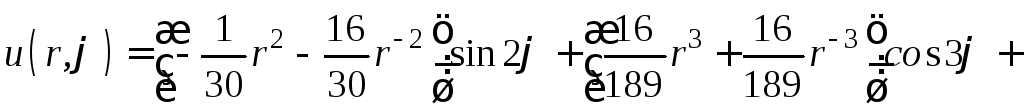
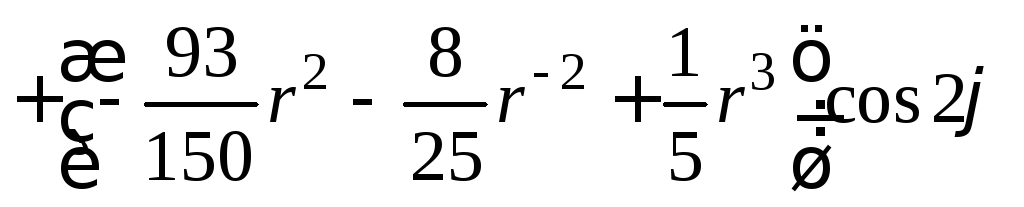 .
.