Пример 5. Найдите общее решение уравнения (задание 4)
.
(8)
Решение. Составляем уравнение характеристик
или
.
Находим
общие интегралы
.
Вводим новые переменные
.
Тогда 
,
,
,
.
После подстановки найденных значений производных в исходное уравнение получим
. (9)
Интегрирование
равенства (9) по переменной
даёт уравнение
,
где
– функция только одной переменной
.
Теперь проинтегрируем уравнение
по переменной
. (10)
Здесь
,
а
и
– функции только одной переменной, то
есть
или
соответственно. Таким образом, если
произвольные функции
и
дважды дифференцируемы, то функция
,
определяемая выражением (10), будет
являться решением уравнения (9). С другой
стороны, всякое решение уравнения (9)
может быть представлено в виде (10) при
соответствующем выборе функций
и
.
Поэтому (10) является общим решением
уравнения (9). Возвращаясь к прежним
переменным, получаем общее решение
уравнения (8) в виде
.
3. Основные уравнения с частными производными. Задачи для уравнений с частными производными
Основные уравнения с частными производными можно условно разбить на два класса: нестационарные (эволюционные) и стационарные. К нестационарным уравнениям относятся волновое уравнение
,
,
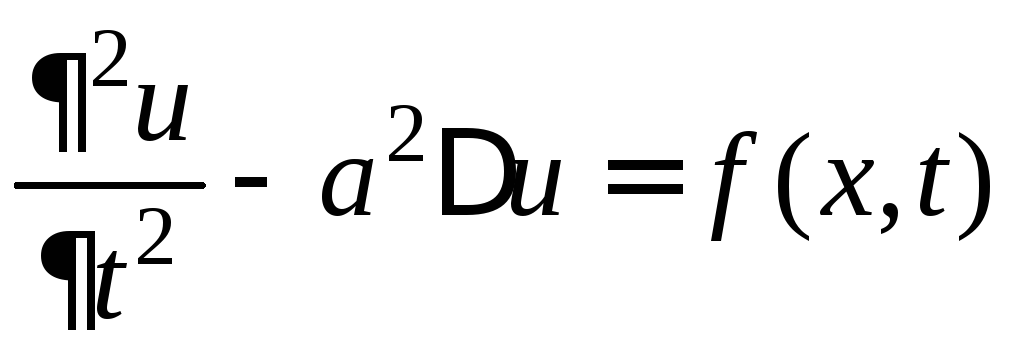и уравнение теплопроводности
.
К стационарным уравнениям относятся уравнение Пуассона
,
уравнение Лапласа
и уравнение Гельмгольца
.
Для
однозначного описания физических
явлений вместе с дифференциальными
уравнениями необходимо ещё задать
дополнительные условия, которые из
множества решений позволили бы выделить
одно искомое решение. Дополнительными
условиями в теории уравнений с частными
производными являются начальные и
граничные условия. В качестве начальных
условий, как правило, задают значения
решения
и его производных при
(в начальный момент времени):
,
.
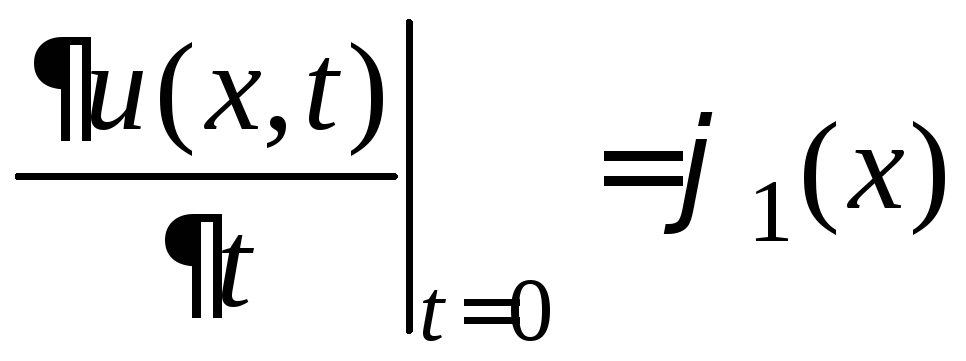Здесь
и
– известные функции. Количество начальных
условий равно порядку старшей производной
по переменной t.
Граничные условия могут быть следующих трёх типов:
1. Граничное
условие I-го
рода, когда
задаётся
значение решения на границе области
.
2. Граничное
условие II-го
рода, когда задаётся значение нормальной
производной решения на границе области
,
где
− внешняя нормаль к поверхности
.
3.
Граничное условие III-го
рода (смешанное граничное условие),
когда на границе области
задаётся линейная комбинация предыдущих
двух граничных условий, то есть
.
Здесь
,
,
,
и
– известные функции.
Различают следующие три основных типа задач для дифференциальных уравнений с частными производными.
1. Задача
Коши для
нестационарных уравнений. Область
является пространством
,
поэтому граничные условия отсутствуют.
Задаются только начальные условия
(область задания
).
2. Краевая
задача для
стационарных уравнений. Задаются
граничные условия на границе S.
Начальные условия отсутствуют (область
задания
).
3. Смешанная
задача для
нестационарных уравнений. Задаются
начальные, граничные условия (область
задания представляет цилиндр вида
)
и условия согласованности
,
.
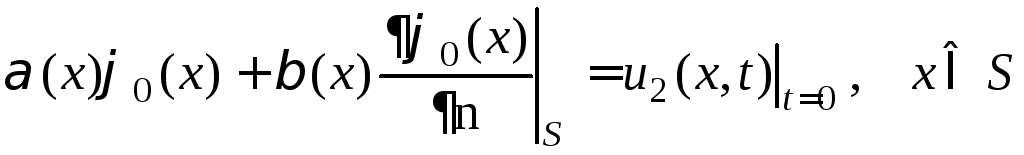