
- •Пример 23. Найдите решение смешанной задачи для однородного волнового уравнения в круге (см. Задание 19)
- •Пример 24. Найдите решение смешанной задачи для однородного волнового уравнения в шаре (задание 20)
- •Пример 25. Найдите решение смешанной задачи для неоднородного волнового уравнения в области
- •Пример 26. Найдите решение смешанной задачи для неоднородного волнового уравнения в интервале (задание 21)
- •Пример 27. Найдите решение смешанной задачи для неоднородного волнового уравнения в прямоугольнике (задание 22)
- •Пример 28. Найдите решение смешанной задачи для неоднородного волнового уравнения в круге (задание 23).
- •Пример 29. Найдите решение смешанной задачи для неоднородного волнового уравнения в шаре (задание 24).
- •Пример 31. Найдите решение смешанной задачи для неоднородного уравнения теплопроводности в интервале (задание 25)
- •Пример 32. Найдите решение смешанной задачи для неоднородного уравнения теплопроводности в круге (задание 26)
- •Пример 33. Найдите решение смешанной задачи для неоднородного уравнения теплопроводности в шаре (задание 27)
- •4.3. Метод интегральных преобразований
- •Пример 34. Найдите решение задачи Коши для неоднородного уравнения теплопроводности
- •Пример 35. Найдите решение задачи Коши для неоднородного уравнения теплопроводности на прямой (задание 28)
- •Пример 36. Найдите решение задачи Коши для неоднородного волнового уравнения
- •Пример 37. Найдите решение задачи Коши для неоднородного волнового уравнения на плоскости (задание 29)
- •Вариант второй
- •Вариант третий
Пример 23. Найдите решение смешанной задачи для однородного волнового уравнения в круге (см. Задание 19)
![]() (1)
(1)
![]() ,
,
 ,
(2)
,
(2)
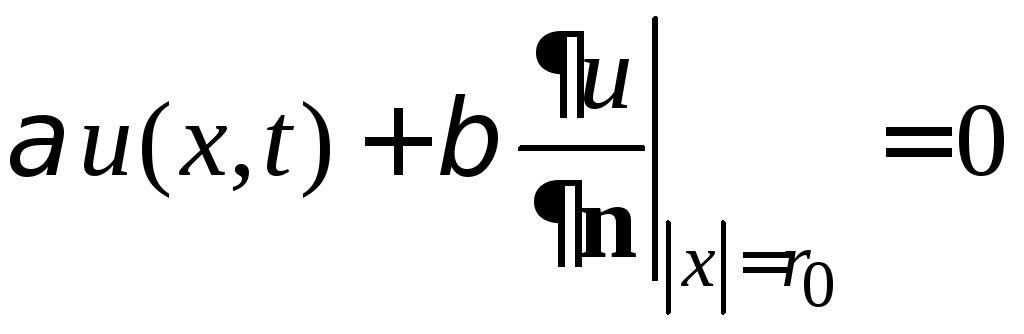 . (3)
. (3)
|
№ |
|
|
|
|
|
|
|
1 |
16 |
4 |
0 |
|
0 |
1 |
|
2 |
1 |
2 |
|
0 |
1 |
0 |
|
3 |
4 |
2 |
0 |
|
2 |
1 |
Решение.
Задачу
удобнее рассматривать в полярных
координатах (![]()
![]() ), так как начальные и граничные условия
не зависят от
), так как начальные и граничные условия
не зависят от
![]() и поэтому решение задачи тоже не будет
зависеть от
и поэтому решение задачи тоже не будет
зависеть от![]()
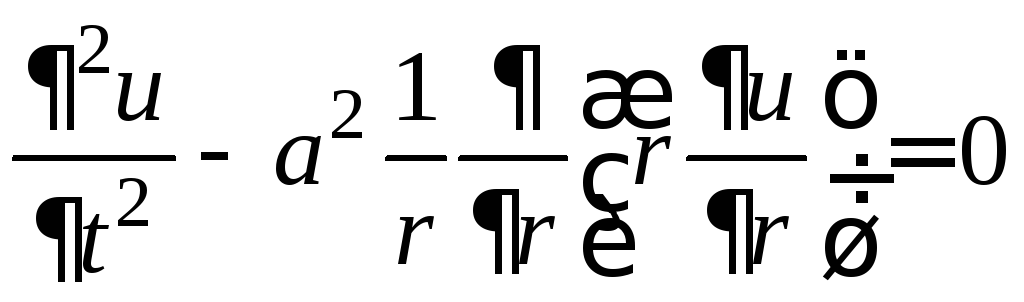 ,
(4)
,
(4)
 ,
(5)
,
(5)
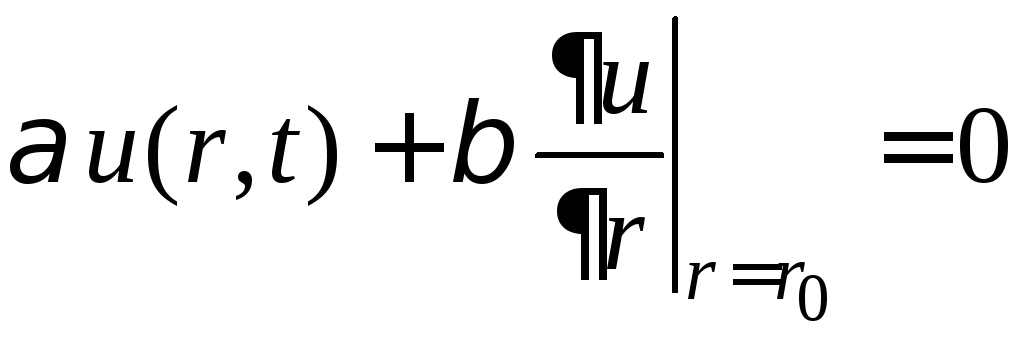 .
(6)
.
(6)
Решение
задачи ищем c
помощью метода Фурье в виде
![]() что приводит к двум обыкновенным
дифференциальным уравнениям
что приводит к двум обыкновенным
дифференциальным уравнениям
![]() ,
,
![]() ,
(7)
,
(7)
![]() .
(8)
.
(8)
Задача (7) представляет собой краевую задачу для уравнения Лапласа в круге (см. пример 11). Собственные функции задачи
![]() ,
,
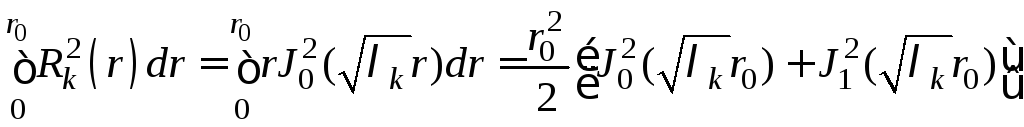 ,
,
где
![]() − корни характеристического уравнениия
− корни характеристического уравнениия
![]() .
.
Первые
пять корней уравнения для заданных
значений
![]() приведены в следующей таблице
приведены в следующей таблице
|
№ |
|
|
|
|
|
|
|
|
|
1 |
0 |
1 |
4 |
0,9176 |
3,0762 |
6,4687 |
11,095 |
16,9551 |
|
2 |
1 |
0 |
2 |
1,4458 |
7,6178 |
18,7218 |
34,7601 |
55,7331 |
|
3 |
2 |
1 |
2 |
0,9102 |
5,2942 |
14,1379 |
27,785 |
46,3249 |
Учитывая
найденные
собственные значения
![]() ,
получимобщее
решение уравнения (8)
,
получимобщее
решение уравнения (8)
![]()
Решение задачи (4) – (6) представим в виде
![]() , (9)
, (9)
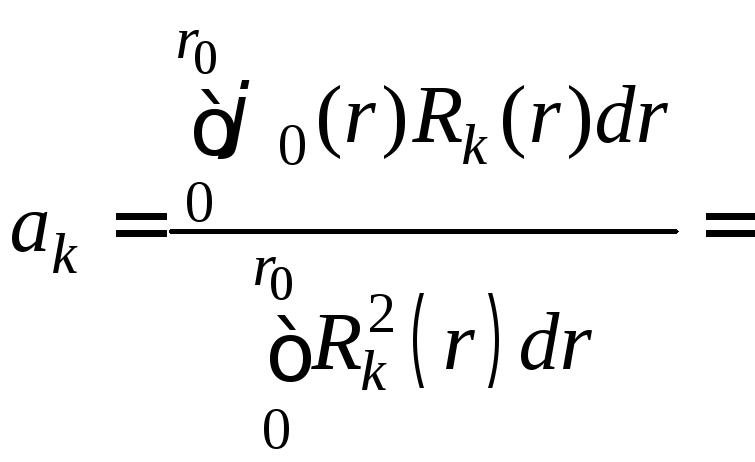
 , (10)
, (10)

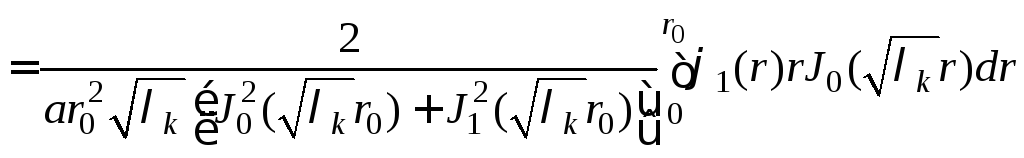 .
(11)
.
(11)
Рассмотрим конкретные варианты, предложенные в условии задачи.
Вариант первый
|
№ |
|
|
|
|
|
|
|
1 |
16 |
4 |
0 |
|
0 |
1 |
Это смешанная задача второго рода
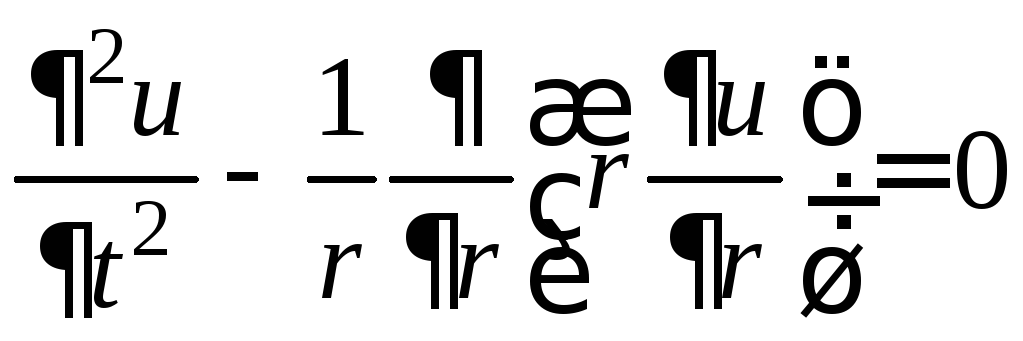 ,
,
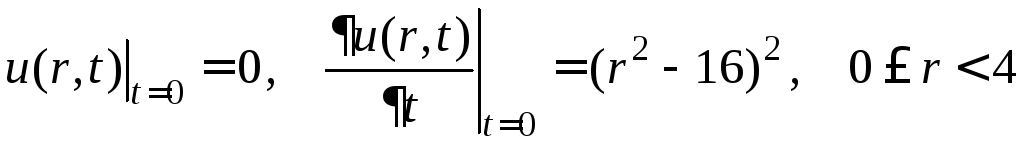 ,
,
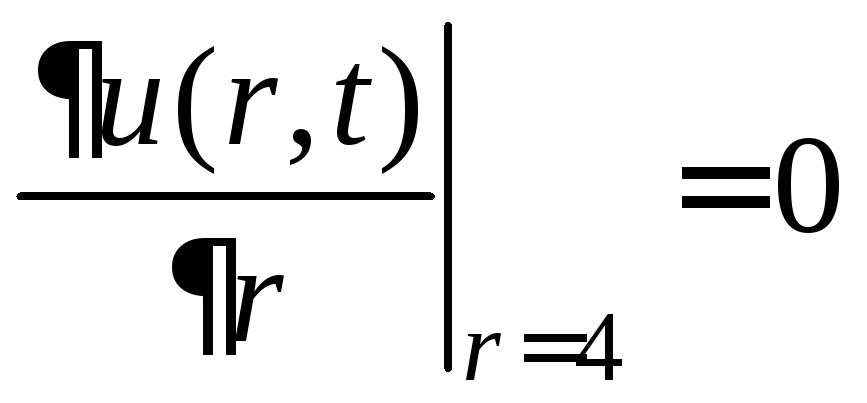 .
.
Находим
коэффициенты
![]() ,
,
![]() ,
для чего подставляем функции
,
для чего подставляем функции
![]() и
и
![]() в
выражения (10) и (11)
в
выражения (10) и (11)
![]() ,
,

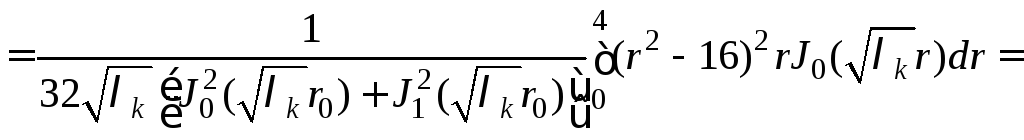
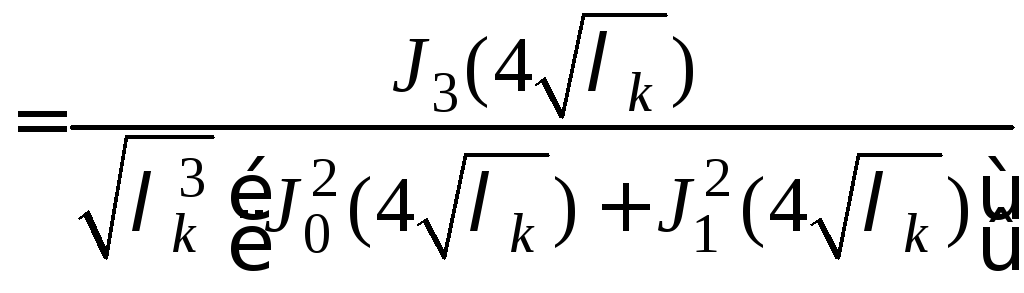 . (12)
. (12)
Интеграл в выражении (12) вычислен с помощью формулы 6.567.1. из [6]
 .
.
Подставляем полученные величины в формулу (6)
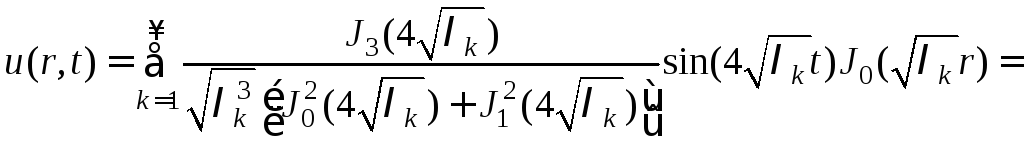
![]()
![]()
![]()
![]()
![]() …
…
Вариант второй
|
№ |
|
|
|
|
|
|
|
2 |
1 |
2 |
|
0 |
1 |
0 |
Это первая смешанная задача
 ,
,
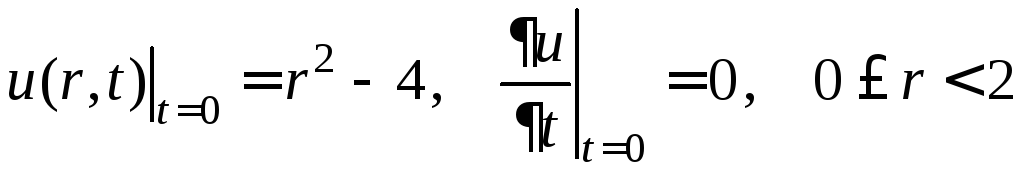 ,
,
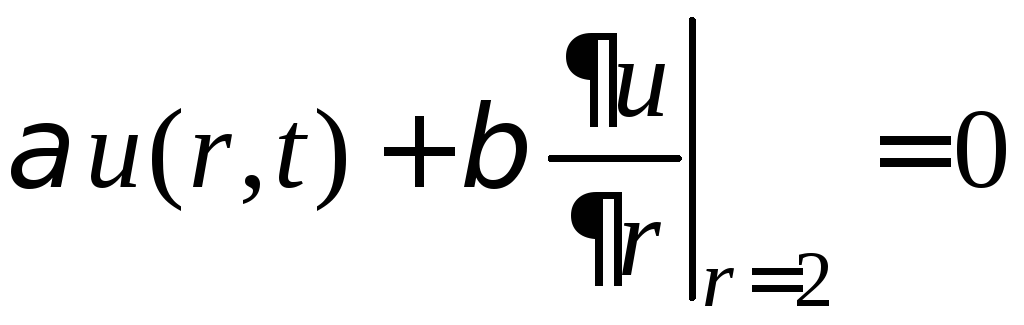 .
.
Находим коэффициенты ряда (9)

 .
.
![]() .
.
Подставляем полученные выражения в формулу (6)
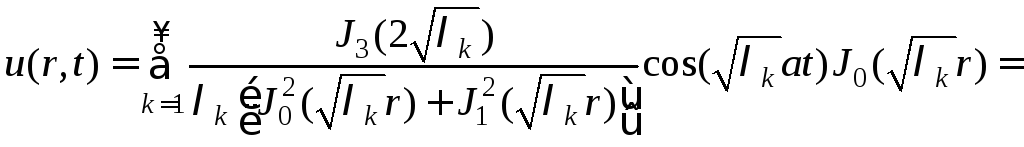
![]()
![]()
![]()
![]()
![]() …
…
Вариант третий
|
№ |
|
|
|
|
|
|
|
3 |
4 |
2 |
0 |
|
2 |
1 |
Это смешанная задача третьего рода
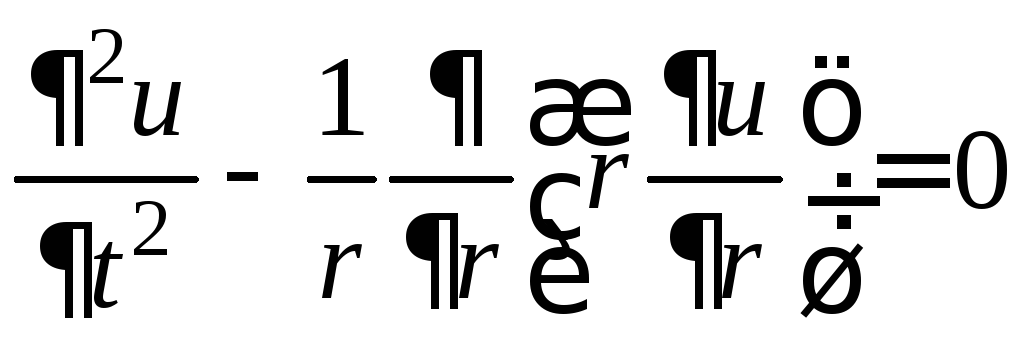 ,
,
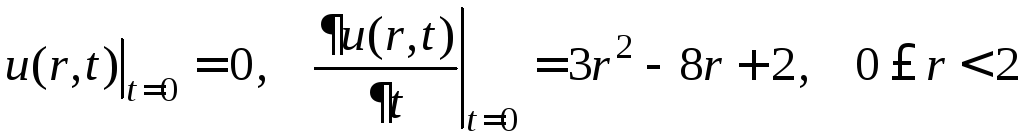 ,
,
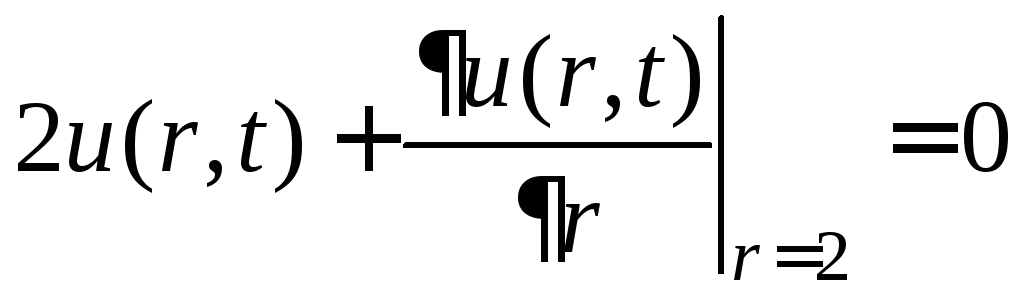 .
.
Находим коэффициенты
![]() ,
,

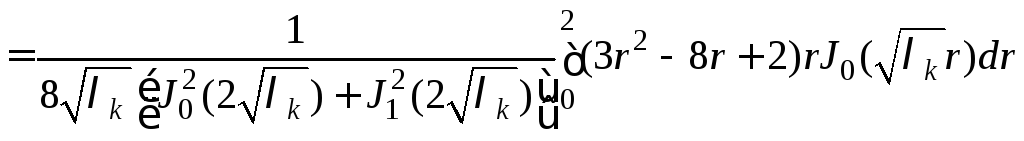 .
.
Подставляем найденные величины в формулу (6) и получаем искомое решение
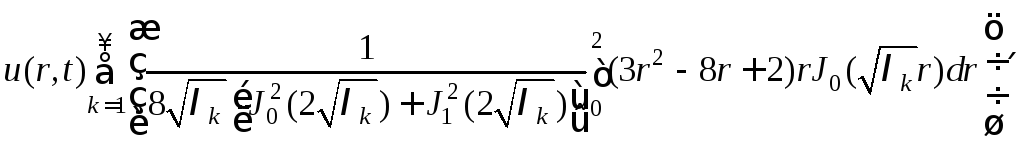
![]()
![]()
![]()
![]()
![]()
![]() …
…
Пример 24. Найдите решение смешанной задачи для однородного волнового уравнения в шаре (задание 20)
![]() (1)
(1)
![]() ,
,
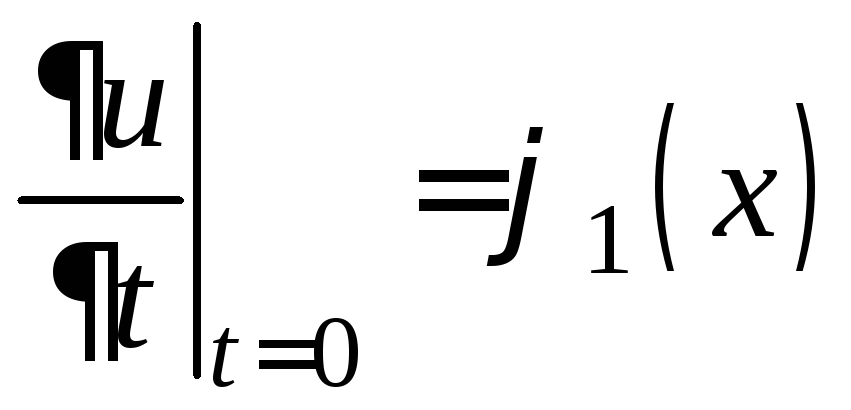 , (2)
, (2)
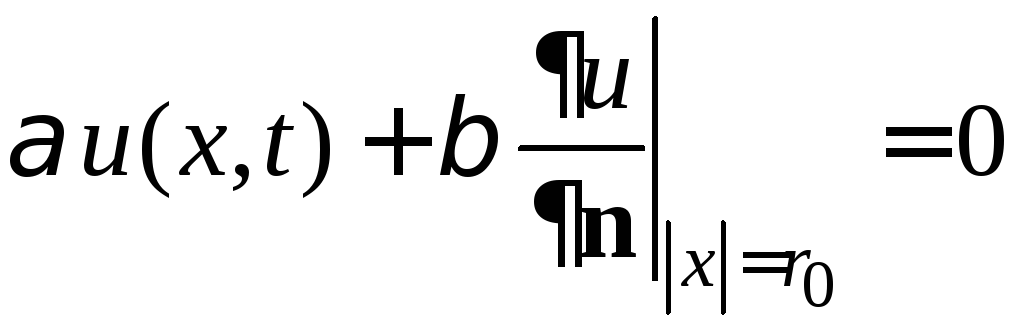 .
(3)
.
(3)
|
№ |
|
|
|
|
|
|
|
1 |
1 |
2 |
|
0 |
1 |
0 |
|
2 |
4 |
3 |
0 |
|
0 |
1 |
|
3 |
9 |
4 |
|
|
1 |
2 |
Решение.
Уравнение
(1), начальные условия (2) и граничное
условие (3) преобразуем в сферические
координаты (![]()
![]() ,
,![]() ).
Начальные и граничные условия не зависят
от
).
Начальные и граничные условия не зависят
от
![]() и
и![]() ,
поэтому задача будет иметь вид
,
поэтому задача будет иметь вид
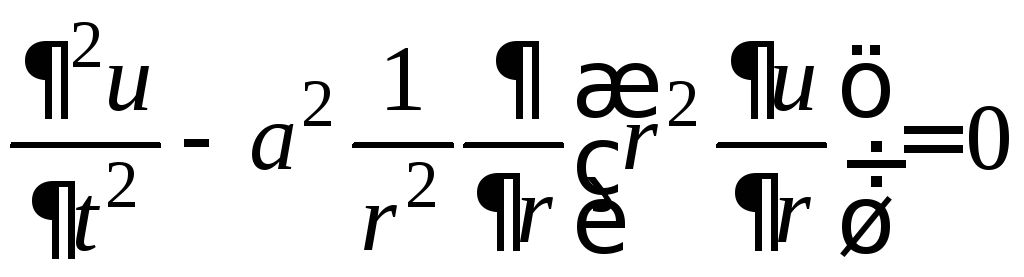 .
(4)
.
(4)
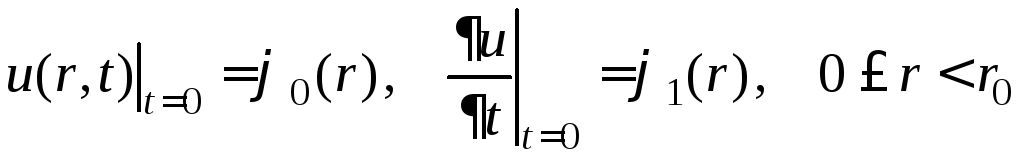 , (5)
, (5)
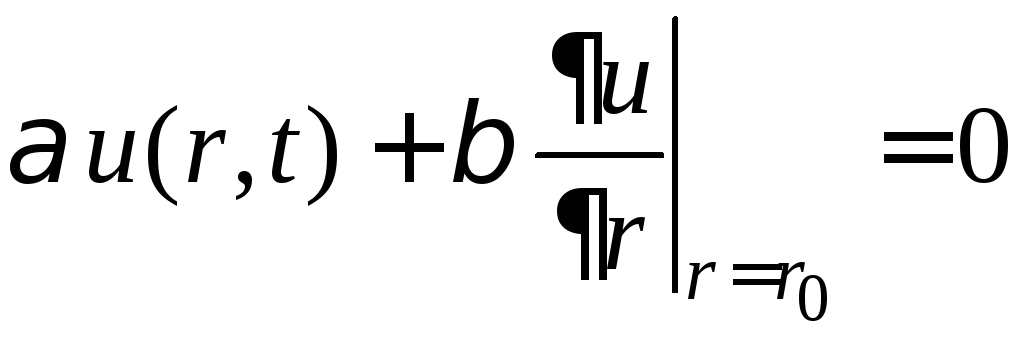 .
(6)
.
(6)
Решение
ищем c
помощью метода Фурье в виде
![]() ,
что приводит к двум обыкновенным
дифференциальным уравнениям
,
что приводит к двум обыкновенным
дифференциальным уравнениям
![]() , (7)
, (7)
![]() .
(8)
.
(8)
Уравнение (7) является уравнением Бесселя (см. п. 4.2.4.) с общим решением
![]() ,
,
где
![]() − сферические функции Бесселя и Неймана.
Так как при
− сферические функции Бесселя и Неймана.
Так как при
![]() ,
то следует положить
,
то следует положить
![]() .
.
Искомое решение приобретает вид
![]() .
.
Для нахождения
собственных значений
![]() ,
воспользуемся граничным условием
,
воспользуемся граничным условием![]() В результате получаем характеристическое
уравнение:
В результате получаем характеристическое
уравнение:
![]() ,
,
первые
пять корней которого для заданных в
условии задачи значений
![]() приведены в следующей таблице.
приведены в следующей таблице.
|
№ |
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
2 |
2,4674 |
9,8696 |
22,2066 |
39,4715 |
61,685 |
|
2 |
0 |
1 |
3 |
2,2434 |
6,6311 |
13,2111 |
21,9842 |
32,9505 |
|
3 |
1 |
2 |
4 |
0,2572 |
1,5089 |
3,9787 |
7,6808 |
12,6156 |
Значит, собственные функции задачи
![]() ,
,
![]()
будут равны
![]() .
.
Учитывая
найденные
собственные значения
![]() ,
получимобщее
решение уравнения (8)
,
получимобщее
решение уравнения (8)
![]() .
.
Решение задачи (4) – (6) представим в виде
![]() ,
(9)
,
(9)
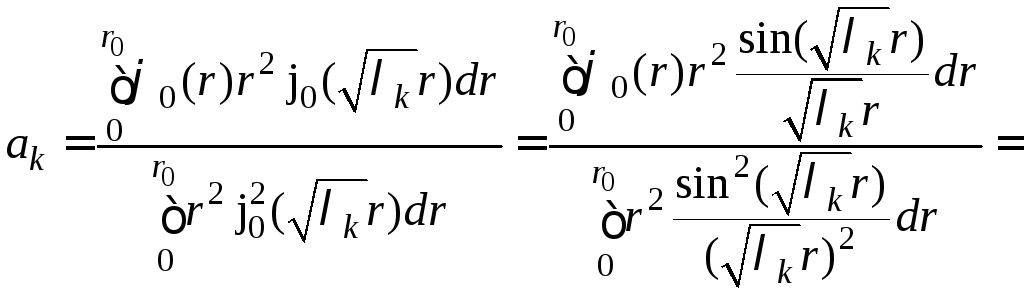
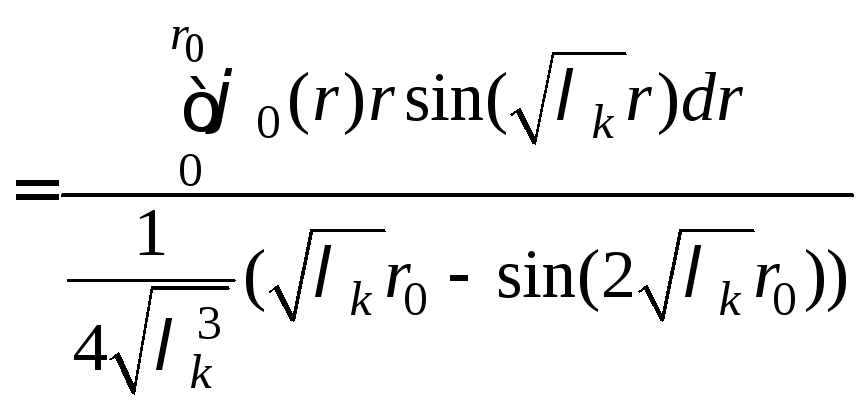 , (10)
, (10)
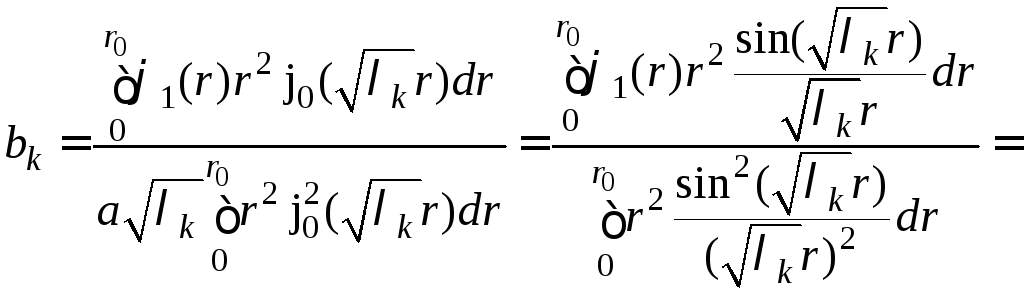
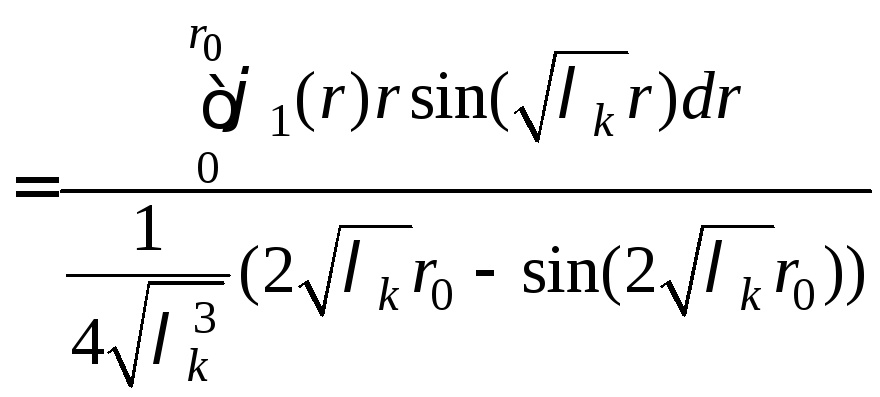 .
(11)
.
(11)
Рассмотрим конкретные варианты, предложенные в условии задачи.
Вариант первый
|
№ |
|
|
|
|
|
|
|
1 |
1 |
2 |
|
0 |
1 |
0 |
Это смешанная задача первого рода
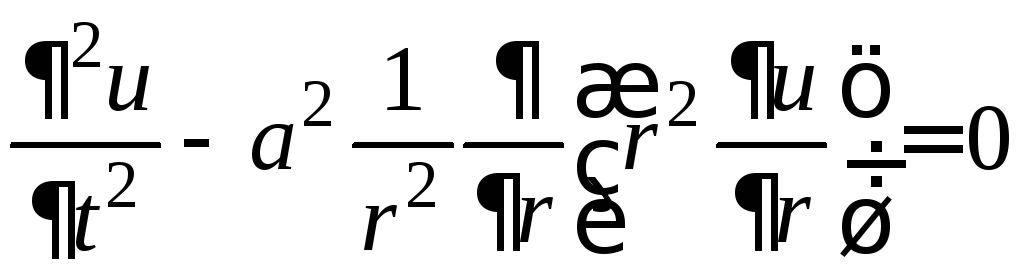 ,
,
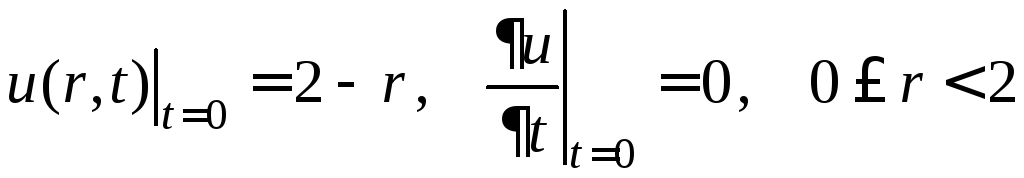 ,
,
![]() .
.
Находим коэффициенты
ряда (9), для чего подставляем функции
![]() и
и![]() в
выражения (10) и (11)
в
выражения (10) и (11)
![]()
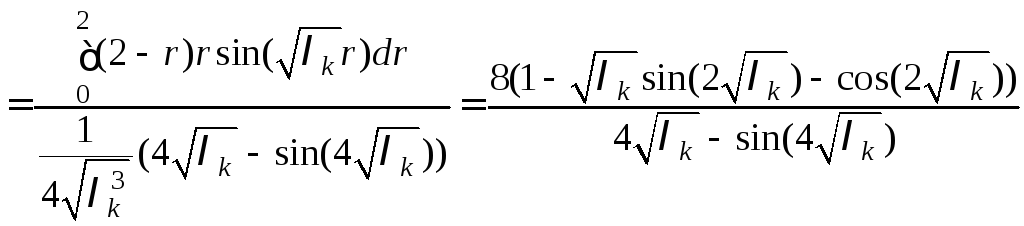 ,
,
![]() .
.
Полученные
выражения для коэффициентов и собственные
значения
![]() подставляем в формулу (9)
подставляем в формулу (9)
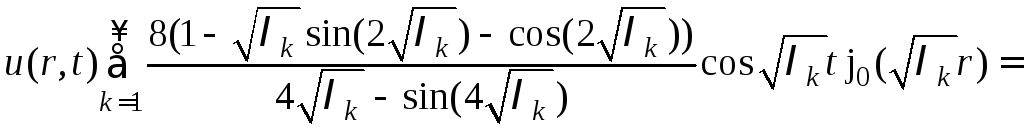
![]()
![]()
![]() …
…
Вариант второй
|
№ |
|
|
|
|
|
|
|
2 |
4 |
3 |
0 |
|
0 |
1 |
Это смешанная задача второго рода
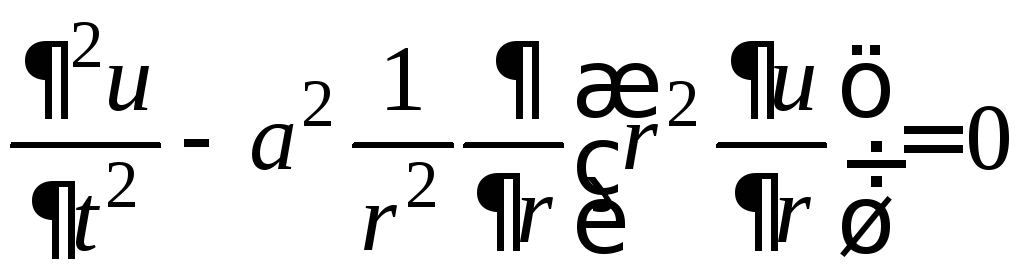 ,
,
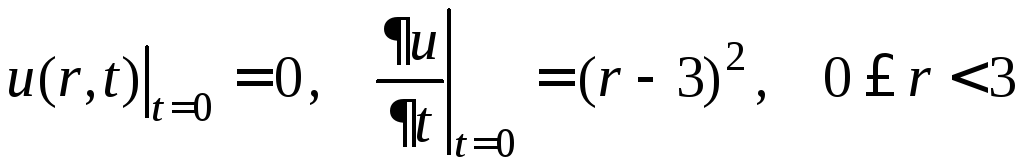 ,
,
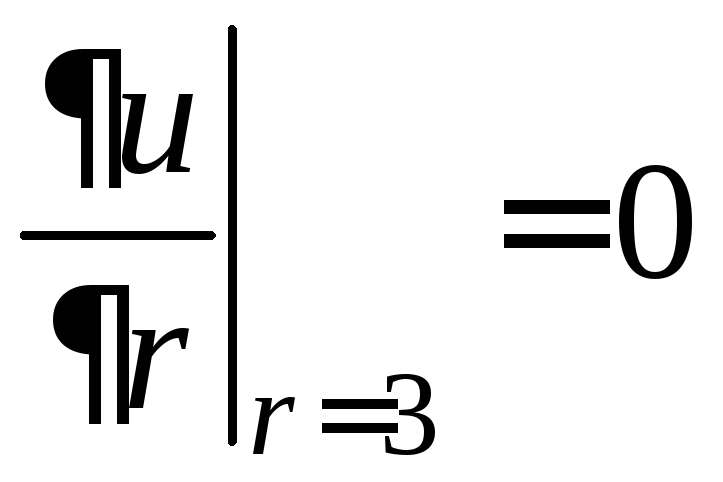 .
.
Находим коэффициенты
![]() ,
,
![]()
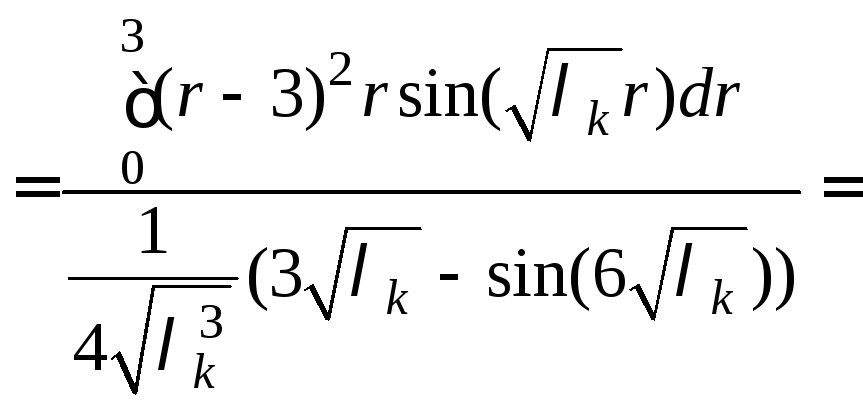
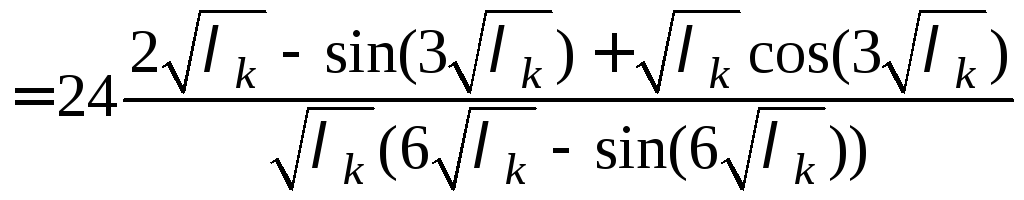
и
подставляем полученные величины и
значения корней характеристического
уравнения
![]() в формулу (9)
в формулу (9)
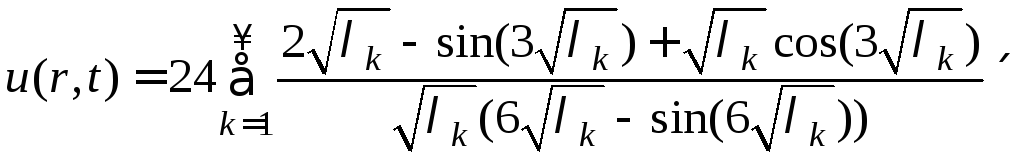
![]()
![]()
![]()
![]()
![]()
![]() …
…
Вариант третий
|
№ |
|
|
|
|
|
|
|
3 |
9 |
4 |
|
|
1 |
2 |
Это смешанная задача третьего рода
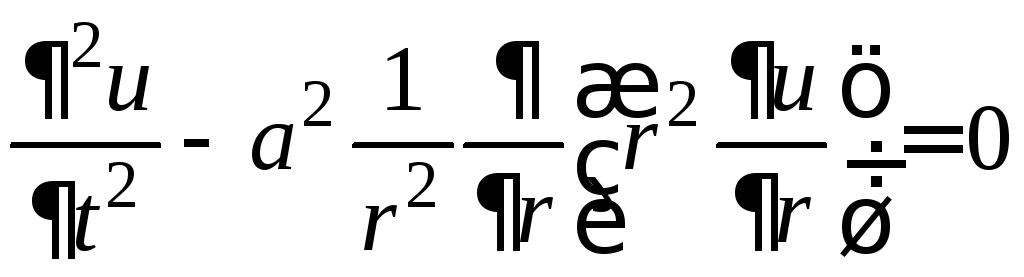 ,
,
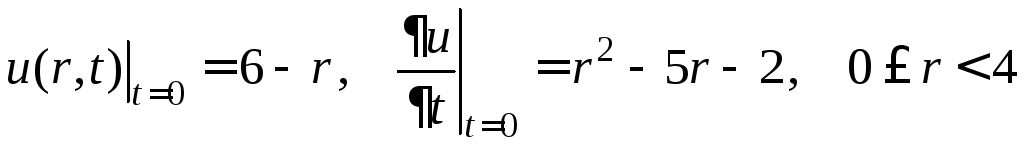 ,
,
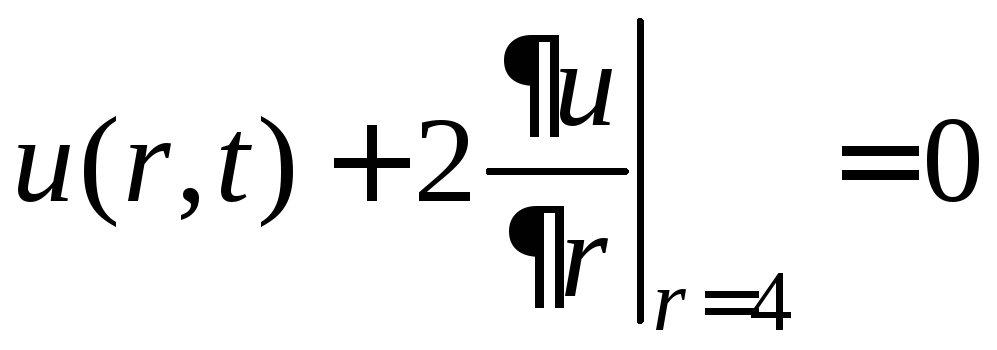 .
.
Находим коэффициенты
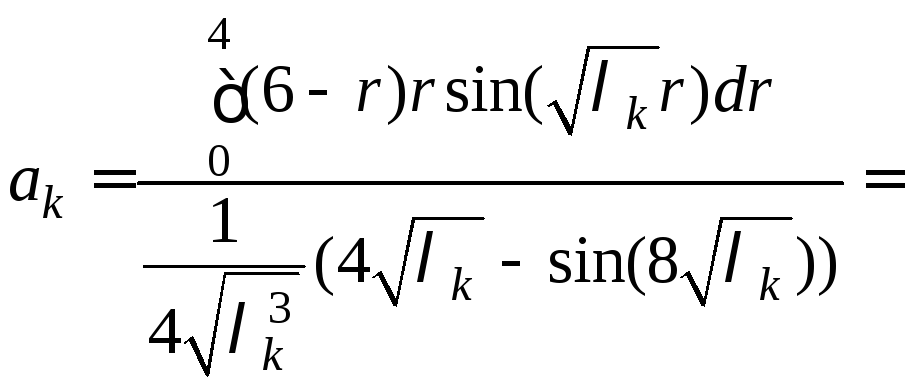
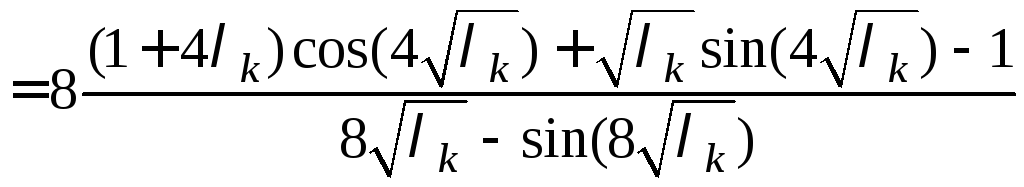 ,
,

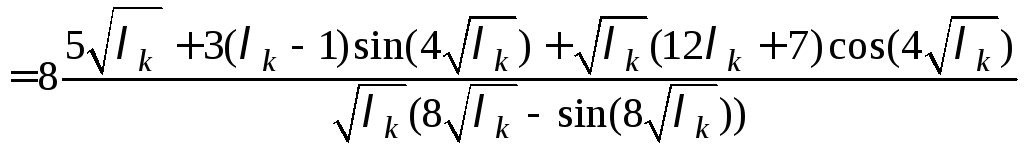 .
.
Подставляем найденные величины коэффициентов и значения корней характеристического уравнения в формулу (9) и получаем искомое решение
![]()

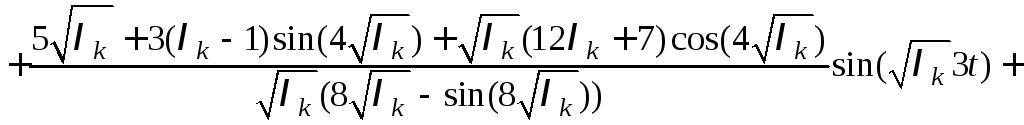
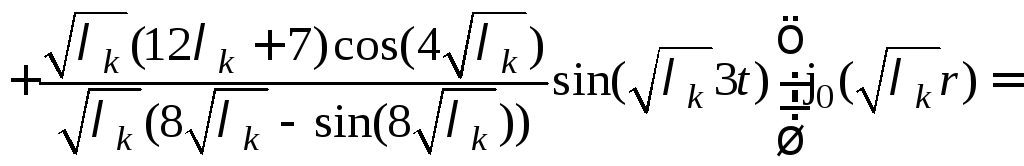
![]()
![]()
![]()
![]()
![]() …
…
