Пример 33. Найдите решение смешанной задачи для неоднородного уравнения теплопроводности в шаре (задание 27)
,
|
№ |
|
|
|
|
|
|
|
1 |
3 |
2 |
|
|
1 |
0 |
|
2 |
3 |
3 |
|
|
0 |
1 |
|
3 |
2 |
4 |
|
|
1 |
2 |
Решение. Преобразуем
задачу в сферические
координаты (
,
).
Начальные и граничные условия не зависят
от
и
.
Поэтому решение задачи тоже не будет
зависеть от
и
.
,
,
.
Решение
задачи, следуя схеме примера 30, ищем в
виде ряда Фурье по собственным функциям
оператораЛапласа
(1)
где
,
(2)
,
(3)
,
(4)
.
(5)
Далее составляем краевую задачу на собственные значения для оператора Лапласа в шаре (см. пример 15)
(6)
Уравнение (6) представляет собой уравнение Бесселя (см. п. 4.2.4). Его общее решение, как известно, определяется выражением
,
где
– сферическая функция Бесселя нулевого
порядка,
– сферическая функция Неймана нулевого
порядка. Из
условия, что решение
должно
быть ограниченным, следует положитьB=0,
так как
при
.
Искомое решение приобретает вид
.
Для
нахождения собственных значений
воспользуемся граничным условием
.
В результате получаем характеристическое
уравнение:
или
.
Первые
пять корней уравнения для заданных
значений
приведены в таблице.
|
№ |
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
2 |
2,4674 |
9,8696 |
22,2066 |
39,4715 |
61,685 |
|
2 |
0 |
1 |
3 |
2,2434 |
6,6311 |
13,2111 |
21,9842 |
32,9505 |
|
3 |
1 |
2 |
4 |
0,6169 |
5,5517 |
15,4213 |
30,2254 |
49,9649 |
Итак, собственные функции оператора Лапласа будут равны
.
Рассмотрим предложенные варианты задачи.
Вариант первый
|
№ |
|
|
|
|
|
|
|
1 |
3 |
2 |
|
|
1 |
0 |
Это смешанная задача первого рода
,
,
.
Характеристическое уравнение задачи на собственные значения для оператора Лапласа
,
собственные значения и собственные функции
Вычисляем с помощью выражений (2) − (5) коэффициенты
,
,
.
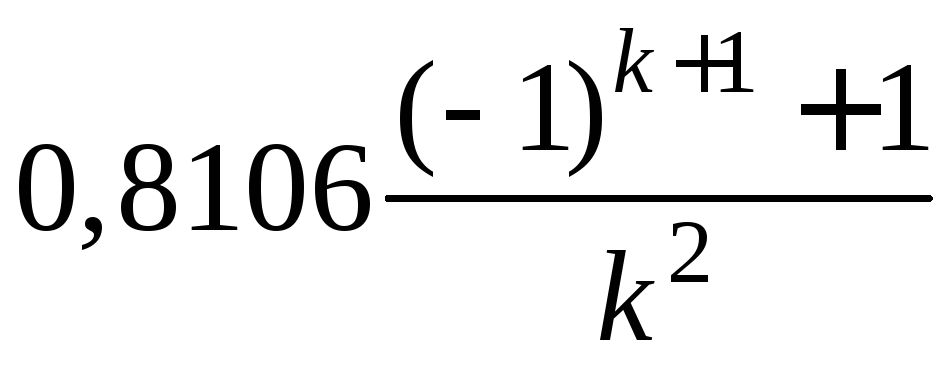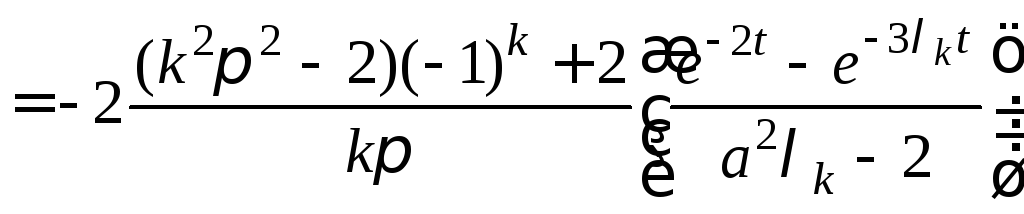Подставляем
найденные значения
,
,
в выражение (1) и получаем решение задачи
Вариант второй
|
№ |
|
|
|
|
|
|
|
2 |
3 |
3 |
|
|
0 |
1 |
Это смешанная задача второго рода
,
.
Характеристическое уравнение задачи на собственные значения для оператора Лапласа
.
Корни уравнения (собственные значения) приведены в табл. 6.5. Собственные функции
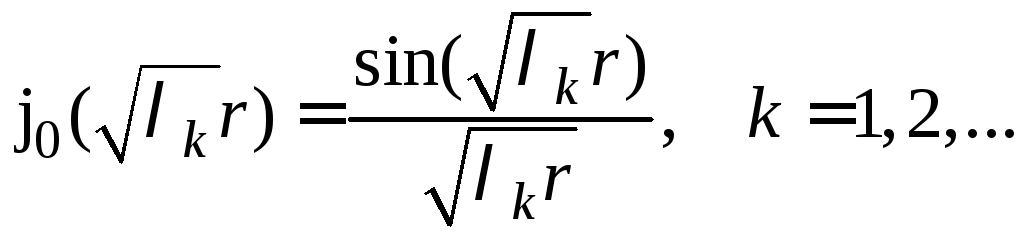
Вычисляем с помощью выражений (2) − (5) коэффициенты
,
.
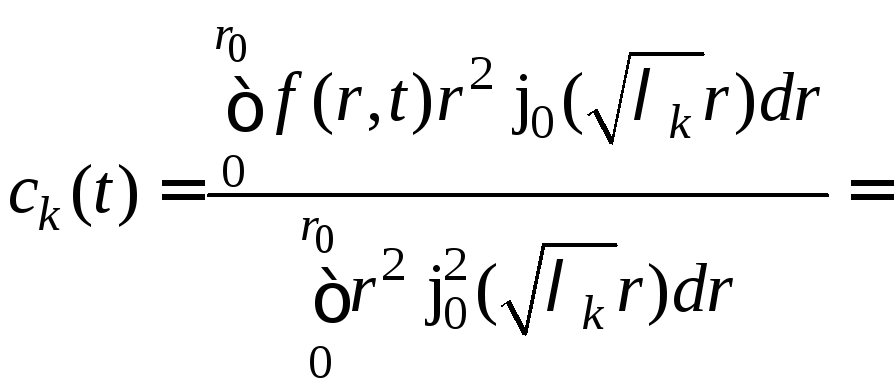
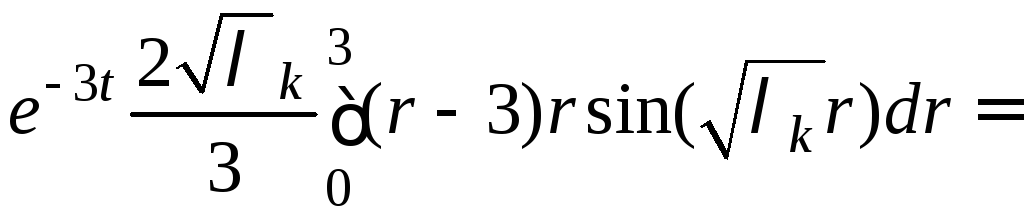
Подставляем
найденные значения
,
,
в выражение (1) и получаем решение задачи
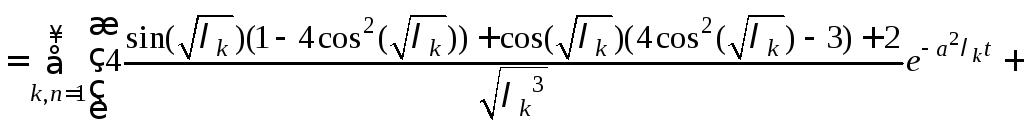
Вариант третий
|
№ |
|
|
|
|
|
|
|
3 |
2 |
4 |
|
|
1 |
2 |
Это смешанная задача третьего рода
,
,
.
Характеристическое уравнение задачи на собственные значения для оператора Лапласа
или
.
Корни уравнения (собственные значения) приведены в табл. 6.4. Собственные функции
Вычисляем с помощью выражений (2) − (5) коэффициенты
,
,
.
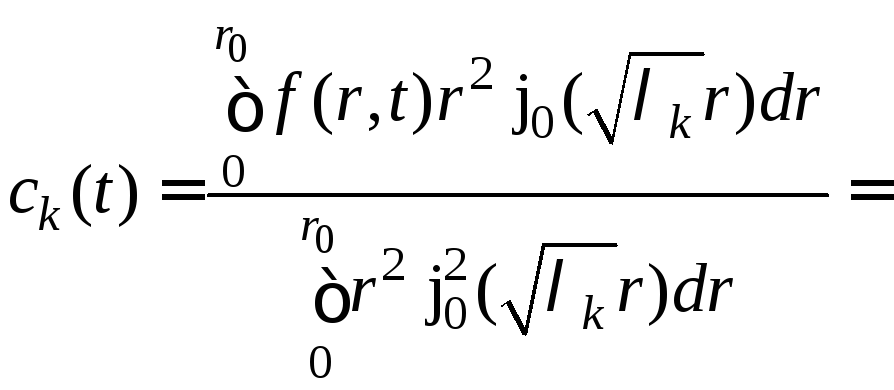
Подставляем
найденные значения
,
,
в выражение (1) и получаем
