II. Уравнения математической физики
1. Определение и классификация дифференциальных уравнений с частными производными
Дифференциальным уравнением с частными производными называется функциональное уравнение вида:
, (1)
где
,
, 
– неизвестная функция,
– вектор
с целочисленными, неотрицательными
координатами (мультииндекс),
– порядок уравнения. Условимся обозначать:
,
где
,
.
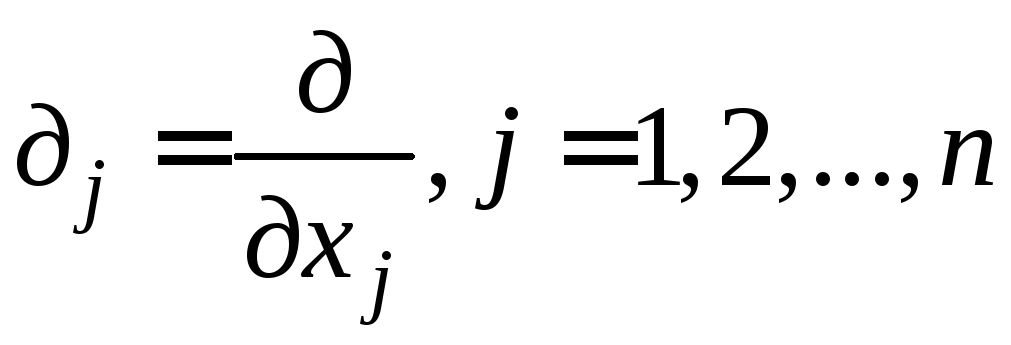Тогда
.
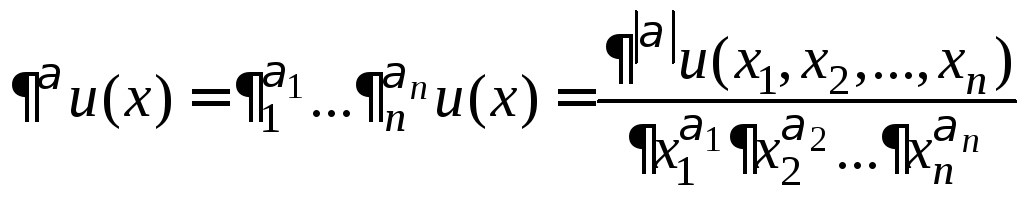При
,
то есть в случае уравнения не выше
второго порядка, будем употреблять
также обозначения:
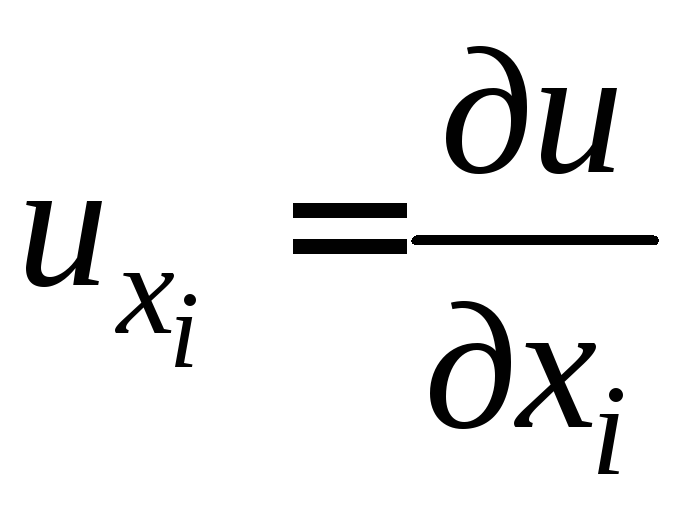и
,
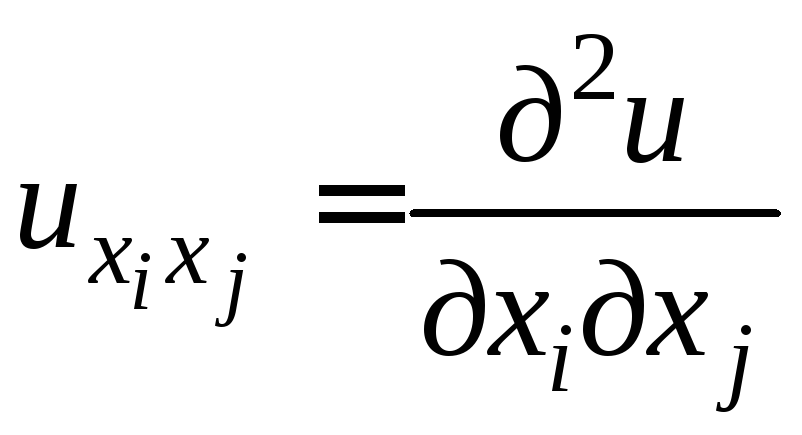а для одной независимой переменной
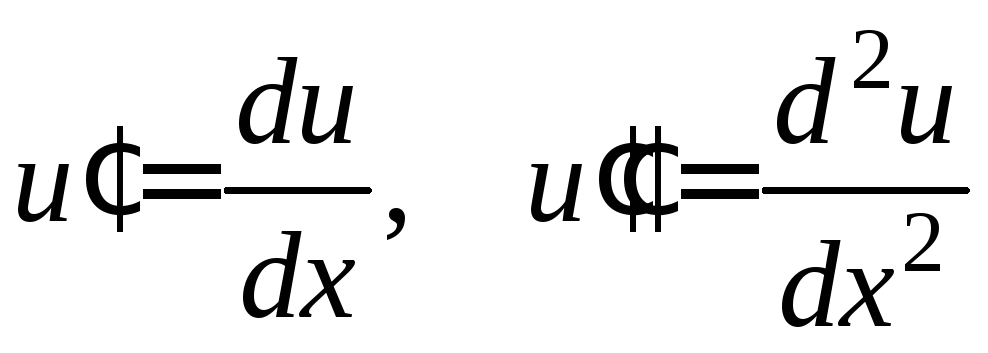и так далее.
Под
классическим (традиционным) решением
уравнения
(1) будем понимать функцию
,
которая при подстановке её в это уравнение
обращает его в тождество. Второй вид
решения – это обобщённое решение. Под
обобщённым решением уравнения (1)
будем понимать такое решение, которое
принадлежит классу обобщённых функций.
Множество всех решений уравнения (1)
называется общим
решением уравнения
(1). Решение называется формальным, если
оно получено без должного обоснования
правомерности используемых при этом
методов.
Уравнение
(1) называется квазилинейным,
если функция
линейна относительно старших производных,
а коэффициенты уравнения при старших
производных зависят только от
В
частном, самом простом случае, уравнение
может быть линейным,
если функция
линейна относительно функции
и её производных, а коэффициенты уравнения
зависят только от переменной 
.
Здесь
– правая часть уравнения. При
уравнение называется однородным
по правой части и принимает следующий
вид:
.
В
противном случае уравнение называется
неоднородным.
Если в указанных уравнениях коэффициенты
,
то они называются уравнениями
с постоянными коэффициентами.
Последующая классификация относится
к квазилинейным уравнениям второго
порядка, которые можно представить в
виде
.
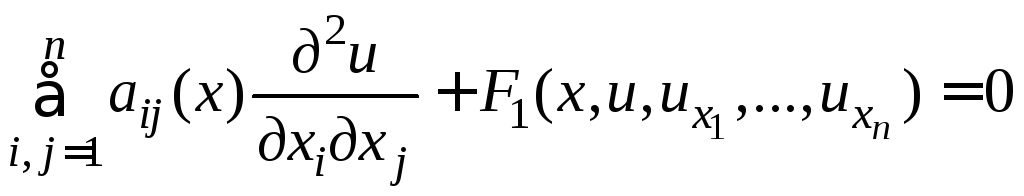В
случае уравнения с двумя независимыми
переменными
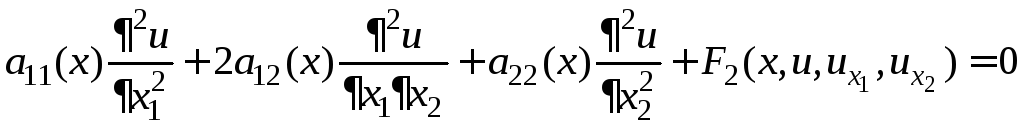(2)
тип уравнения определяется знаком определителя
.
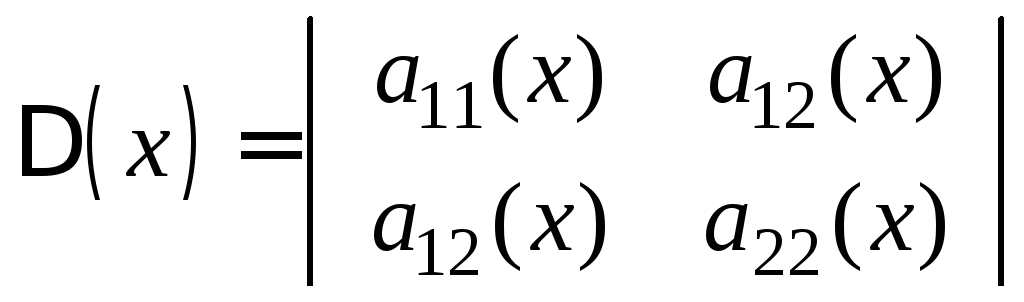Возможны
три различных случая (при
):
1.
. В
этом случае уравнение (2) называется
уравнением
эллиптического
типа (в точке
).
2.
.Тогда
уравнение (2) называется уравнением
гиперболического
типа (в точке
).
3.
. В
этом случае уравнение (2) – уравнение
параболического типа
(в точке
).
Замечание. Если
уравнение (2)
является эллиптическим,
гиперболическим
или параболическим в каждой точке
области
,
то оно называется
эллиптическим, гиперболическим или
параболическим во всей области
.
Для
классификации квазилинейных уравнений
второго порядка при числе независимых
переменных
можно использовать теорию квадратичных
форм. В курсе линейной алгебры доказывается,
что квадратичную форму всегда можно
привести к каноническому виду
.
(3)
Тип
уравнения в данной точке
определяется следующим образом.
1.
Пусть в квадратичной форме (3)
.
Тогда она определяет уравнение
эллиптического
типа в точке
,
если все слагаемые одного знака (
или
)
и уравнение
гиперболического
(нормально-гиперболического)
типа, если
одно из слагаемых по знаку отличается
от остальных
(
или
).
Если несколько слагаемых по знаку
отличаются от остальных, то есть
и
,
то уравнение
называется
ультрагиперболическим.
2.
Если в квадратичной форме (3)
,
то она определяет уравнение
параболического
типа, а при
и
или
–
нормально-параболического типа.
Пример 1. Определите, какие из приведенных уравнений являются нелинейными, квазилинейными или линейными (однородными или неоднородными). Укажите порядок уравнения (задание 1).
а)
,
б)
,
в)
,
г)
Решение.
а) Уравнение нелинейное, так как
коэффициенты при вторых производных
являются функциями не только независимых
переменных, но и функции
.
Это уравнение второго порядка.
б) Это уравнение квазилинейное, так как коэффициент при второй производной зависит только от независимых переменных. Порядок уравнения равен двум.
в)
Это неоднородное линейное уравнение,
так как коэффициенты при производных
и неизвестной функции зависят только
от независимых переменных и
.
Данное уравнение–
уравнение третьего порядка.
г)
Это однородное линейное уравнение, так
как коэффициенты при производных и
неизвестной функции зависят только от
независимых переменных и
.
Порядок уравнения равен двум.
Пример 2. Определите тип следующих уравнений (задание 2):
а)
,
б)
,
в)
,
г)
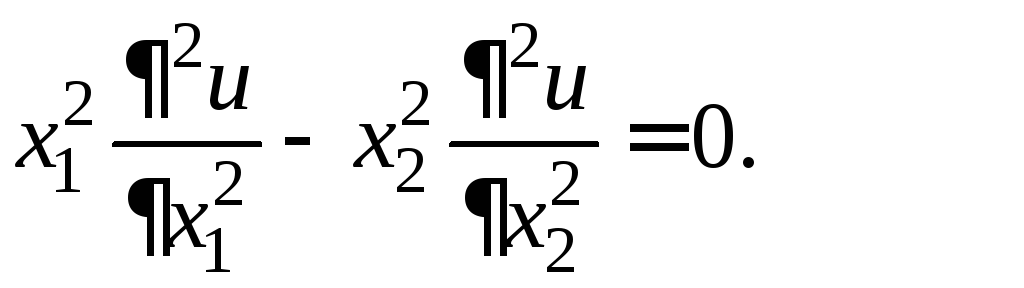
Решение. а) Коэффициенты уравнения
Определитель
.
Значит,
это уравнение гиперболического типа в
.
б)
Данное уравнение является уравнением
гиперболического типа при
и эллиптического типа при
,
так как
.
в)
Это уравнение параболического типа в
,
так как
в
.
г)
Определитель
в
.
Поэтому это уравнение гиперболического
типа в
.