4.3. Метод интегральных преобразований

Одним из эффективных методов, позволяющих упростить решение краевых задач для уравнений с частными производными, является метод интегральных преобразований. Так после - кратного применения интегрального преобразования дифференциальное уравнение спеременными сводится к дифференциальному уравнению спеременными. И, в частности, приполучается обыкновенное дифференциальное уравнение. К решению полученного уравнения применяют затем обратное интегральное преобразование и в результате получают решение исходного уравнения. Метод интегральных преобразований применяют для решения краевых задач для уравнений с частными производными всех типов.

Пример 34. Найдите решение задачи Коши для неоднородного уравнения теплопроводности

, (1)

. (2)

где , .

Решение. Применим к равенствам (1) и (2) преобразование Фурье по переменным . В результате получим

, (3)

, (4)

где

,

.

Итак, задача Коши (1) − (2) для уравнения с частными производными с помощью преобразования Фурье редуцировалась в задачу Коши (3) − (4) для обыкновенного дифференциального уравнения 1-го порядка. Решение этой задачи представим в виде

. (5)

Применение обратного преобразования Фурье к (5) даёт решение задачи Коши (1) − (2)

. (6)

Выражение (6) называется формулой Пуассона.

Пример 35. Найдите решение задачи Коши для неоднородного уравнения теплопроводности на прямой (задание 28)

, (1)

. (2)

Решение. Подставляем в формулу Пуассона заданные функции

. (3)

Рассмотрим первый интеграл

.

Выделим полный квадрат в выражении, стоящем в показателе экспоненты

и введём новую переменную

.

Тогда получим

.

Учитывая известную формулу

,

находим окончательное значение первого интеграла в выражении (3)

.

Во втором интеграле

делаем замену

и получаем

,

так как

, .

Подставляем найденные значения интегралов в формулу Пуассона и получаем решение заданной задачи

.

Пример 36. Найдите решение задачи Коши для неоднородного волнового уравнения

, (1)

. (2)

где , ,.

Решение. С помощью преобразования Фурье по переменной задачу Коши (1) − (2) сводим к задаче Коши для обыкновенного дифференциального уравнения

,

,

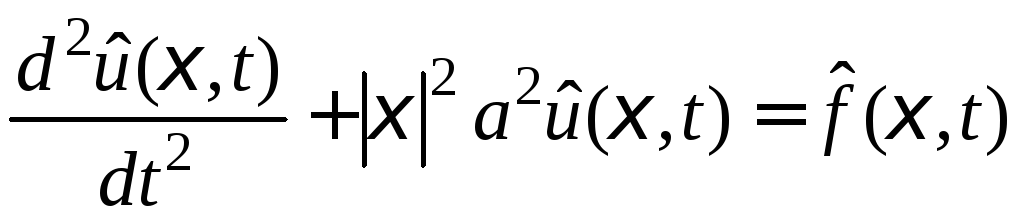где

.

Решение этой задачи представим в виде

. (3)

.

Применение обратного преобразования Фурье к (3) даёт решение задачи Коши (1) − (2)

. (4)

В случае выражение (4) даёт формулу Даламбера

,

при формулу Пуассона

,

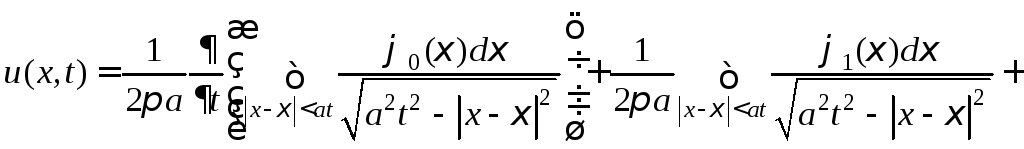
при формулу Кирхгофа

.

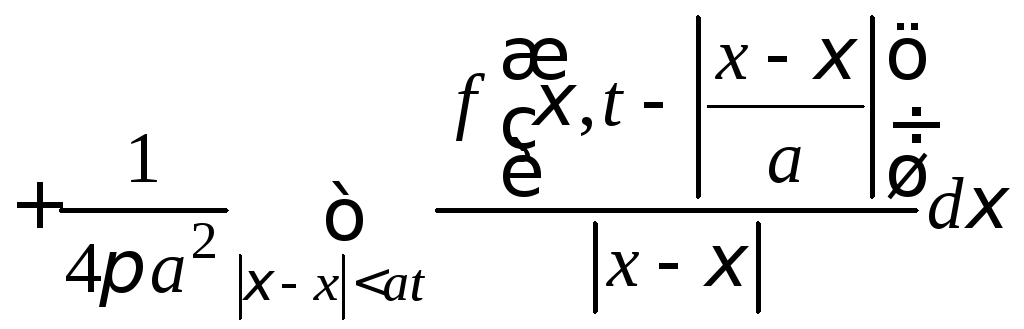Пример 37. Найдите решение задачи Коши для неоднородного волнового уравнения на плоскости (задание 29)

, , ,

, .

№
1	4
2	16			0
3	9		0

Решение задачи находим с помощью формулы Пуассона. Рассмотрим конкретные варианты.

Вариант первый

№
1	4

Подставляем в формулу Пуассона заданные функции , , и получаем

.

Область интегрирования по переменной представляет собой круг. Поэтому перейдём к полярным координатам

.

В результате получаем

.

Вариант второй

№
2	16			0

Подставляем в формулу Пуассона

, ,

и получаем

.

В полярных координатах

.

Вариант третий

№
3	9		0

Подставляем в формулу Пуассона

, ,

и получаем

.

В полярных координатах

.

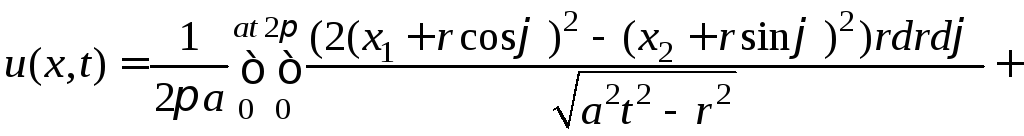
Пример 38. Найдите решение задачи Коши для неоднородного волнового уравнения в пространстве (задание 30)

,

.

№
1	4			0
2	16		0	0
3	4		0

Решение задачи Коши для неоднородного волнового уравнения в пространстве даётся формулой Кирхгофа

.

Рассмотрим предложенные варианты задачи.

Вариант первый

№
1	4			0

Подставляем в формулу Кирхгофа заданные функции , , и получаем

. (1)

Вычислим первый интеграл в выражении (1). В нашем случае поверхность представляет собой сферу

.

Разбиваем её на две полусферы

: ,

: .

В результате получаем

. (2)

Уравнения поверхностей и заданы в явном виде

.

Поэтому поверхностные интегралы вычисляем по формуле

, (3)

где − область интегрирования, представляющая собой круг

.

Подставляем интегралы (2) в формулу (3)

.

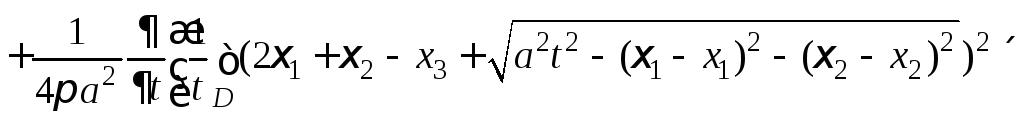
В полярных координатах

интегралы преобразуются следующим образом:

. (4)

Второй интеграл в выражении (1) вычислим, перейдя к сферическим координатам

. (5)

Подставим выражения (4) и (5) в формулу (1) и получим решение заданной задачи

+.