Пример 25. Найдите решение смешанной задачи для неоднородного волнового уравнения в области

(1)

, , (2)

, (3)

где , ,

Решение поставленной задачи представим в виде ряда Фурье

(4)

где (x) – собственные функции оператора , то есть решения краевой задачи на собственные значения для оператора Лапласа в областиG

(5)

. (6)

Неизвестные функции можно найти следующим образом. Умножим равенство (1) скалярно на.

(7)

и выполним следующие преобразования

(8)

.

Согласно (22) (см. п.4.2.6.)

.

Поэтому

. (9)

Равенство (7) с учётом (6), (8) и (9) принимает вид

, (10)

. (11)

Аналогично преобразуются начальные условия (2)

,

,

или с учётом (6)

,

,

откуда

(12)

Итак, функция представляет собой решение задачи Коши (10), (12). Общее решение уравнения (10), согласно теории обыкновенных дифференциальных уравнений, можно представить в виде

, (13)

где – общее решение однородного уравнения

, (14)

а – какое-либо частное решение неоднородного уравнения

. (15)

Общее решение уравнения (14) имеет вид

. (16)

Какое-либо частное решение уравнения (15) найдём методом вариации постоянных. Приводим окончательный результат.

(17)

Выражение (13) после подстановки в него (16) и (17) даст общее решение уравнения (15)

(18)

Значения неизвестных констант иполучим с помощью начальных условий (12)

(19)

. (20)

Подставим (18) в (4) и получим решение смешанной краевой задачи (1) – (3):

(21)

Теорема. Пусть выполняются следующие условия:

1. 

2. и – кусочно-непрерывны на, ;

3. .

Тогда решение задачи(1) – (3) существует, единственно и устойчиво, а при выполнении условия

4. 

определяется выражением (21).

Пример 26. Найдите решение смешанной задачи для неоднородного волнового уравнения в интервале (задание 21)

.

№
1	9		2			1	0	1	0
2	1		1		0	1	0	0	1
3	4		5	0		2	1	1	2

Решение. Предложенная задача является частным случаем задачи (), рассмотренной в примере 25. Поэтому решение будем искать в виде ряда Фурье по собственным функциямоператораЛапласа

(1)

где

, (2)

, , (3)

. (4)

Далее составляем краевую задачу на собственные значения для оператора Лапласа. В данном случае это будет задача Штурма -Лиувилля (см. пример 10)

с характеристическим уравнением

и решениями в виде

или

.

Рассмотрим конкретные варианты, предложенные в условии задачи.

Вариант первый

№
1	9		2			1	0	1	0

Задача Штурма - Лиувилля для этих параметров (см. решение примера 10)

,

,

характеристическое уравнение

,

собственные функции и собственные значения

Находим коэффициенты ,,и

,

;

,

.

Подставляем найденные значения ,,,в выражение (1) и получаем искомое решение

Вариант второй

№
2	1		1		0	1	0	0	1

Задача Штурма - Лиувилля для заданных параметров

,

характеристическое уравнение

,

собственные функции и собственные значения

Находим соответственно

,

,

,

.

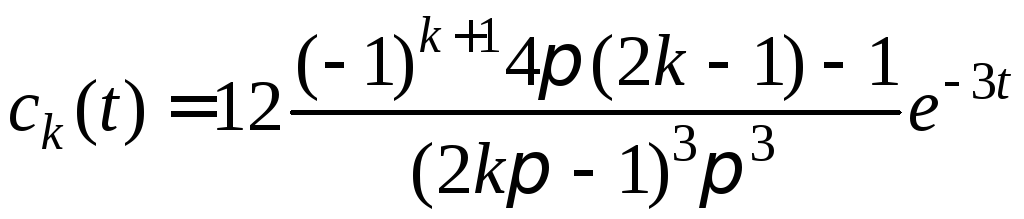Подставляем найденные значения ,,,в выражение (1) и получаем решение задачи

Вариант третий

№
3	4		5	0		2	1	1	2

Задача Штурма - Лиувилля для этих параметров

с характеристическим уравнением

,

первые пять корней которого приведены в таблице.

	1	2	3	4	5
	0,1941	0,9036	2,2675	4,347	7,1742
	8,209	0,7412	−0,3734	0,114	−0,0488
	3,2687	−0,3545	−0,2935	0,0742	−0,0376

Собственные функции, соответствующие найденным собственным значениям

или

.

Находим соответственно

,

,

,

.

Подставляем найденные значения ,,,в выражение (1) и получаем

…
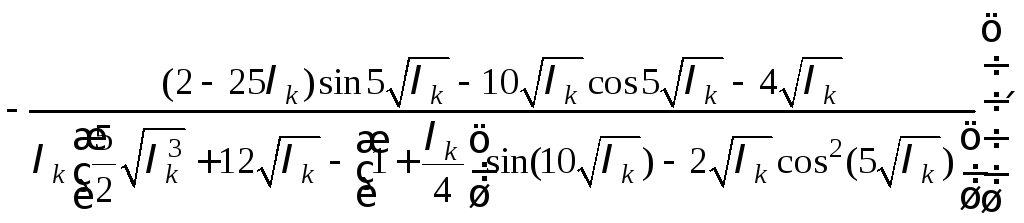