
- •II. Уравнения математической физики
- •1. Определение и классификация дифференциальных уравнений с частными производными
- •2. Характеристические поверхности (характеристики) квазилинейного уравнения второго порядка. Приведение квазилинейного уравнения второго порядка к каноническому виду
- •Пример 3. Приведите к каноническому виду уравнения (задание 3):
- •Пример 4. Упростите уравнения:
- •Пример 5. Найдите общее решение уравнения (задание 4)
- •3. Основные уравнения с частными производными. Задачи для уравнений с частными производными
- •4. Методы решения задач для уравнений с частными производными
- •4.1. Метод характеристик
- •4.1.1. Метод Даламбера
- •Пример 6. Найдите решение задачи Коши для однородного волнового уравнения на прямой
- •4.1.2. Фазовая плоскость
- •Вариант первый
- •Решение задачи находится по формуле Даламбера
- •Вариант второй
- •4.2. Метод разделения переменных (метод Фурье)
- •4.2.1. Ортогональные системы
- •4.2.2. Функции Бесселя
- •4.2.3. Модифицированные функции Бесселя
- •4.2.4. Сферические функции Бесселя
- •4.2.5. Шаровые и сферические функции
- •4.2.6. Схема метода Фурье
- •Пример 10. Найдите решения задачи Штурма - Лиувилля (задание 8)
- •Пример 11. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в круге
- •Пример 12. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в прямоугольнике (задание 9)
- •Пример 13. Найдите решение краевой задачи для уравнения Лапласа в круге (задание 11)
- •Пример 14. Найдите решение краевой задачи для уравнения Лапласа в прямоугольнике (задание 10)
- •Вариант первый
- •Вариант второй
- •Вариант третий
- •Пример 15. Найдите решение краевой задачи для уравнения Лапласа в шаре (задание 12)
- •Вариант третий
- •Пример 16. Найдите решение краевой задачи для уравнения Лапласа в цилиндре (задание 13)
- •Пример 17. Найдите решение краевой задачи для уравнения Пуассона в кольце (задание 14)
- •Пример 18. Найдите решение краевой задачи для уравнения Гельмгольца в круге (задание 15)
- •Имеем краевую задачу третьего рода
- •Пример 19. Найдите решение краевой задачи для уравнения Гельмгольца в шаре (задание 16)
- •Пример 21. Найдите решение смешанной задачи для однородного волнового уравнения в интервале (см. Задание17)
- •Пример 22. Найдите решение смешанной задачи для однородного волнового уравнения в прямоугольнике (задание 18)
4.2.5. Шаровые и сферические функции
Шаровыми функциями называются решения дифференциального уравнения
![]() , (20)
, (20)
называемого
уравнением
Лежандра.
Здесь
![]() ,
,
![]() и
и
![]() могут принимать любые значения. Частными
видами шаровых функций являются функции
Лежандра первого рода
могут принимать любые значения. Частными
видами шаровых функций являются функции
Лежандра первого рода
![]() и функции
Лежандра второго рода
и функции
Лежандра второго рода
![]() .
Эти функции при
.
Эти функции при
![]() определяются выражениями:
определяются выражениями:
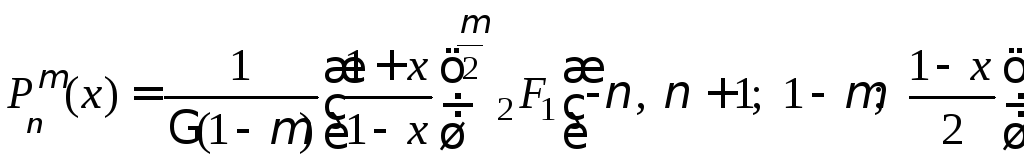 ,
,
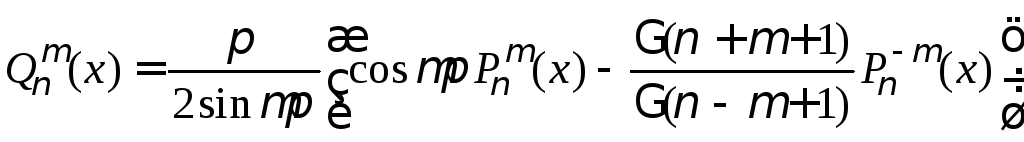 ,
,
где

или в виде интеграла
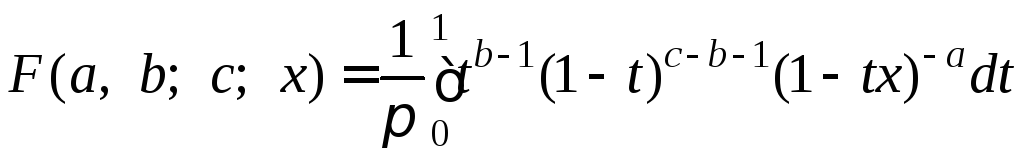 .
.
Здесь
![]() – гипергеометрическая функция.
– гипергеометрическая функция.
При
![]() уравнение (20) принимает вид
уравнение (20) принимает вид
![]() .
.

Рис. 4.8
Решения этого уравнения
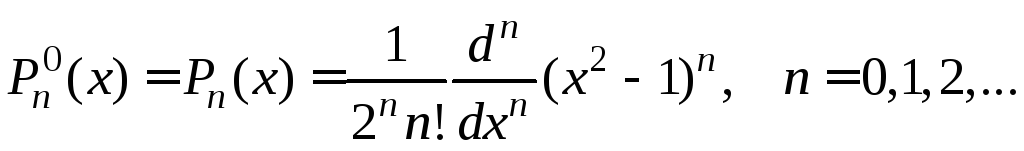 (21)
(21)
называются полиномами Лежандра. Формула (21) называется формулой Родрига. С помощью формулы (21) получаем
![]() ,
,
![]()
На рис.4.8 представлены графики полиномов Лежандра (цифры соответствуют порядку полинома).
Полиномы
Лежандра в пространстве
![]() ортогональны с весом
ортогональны с весом
![]() :
:
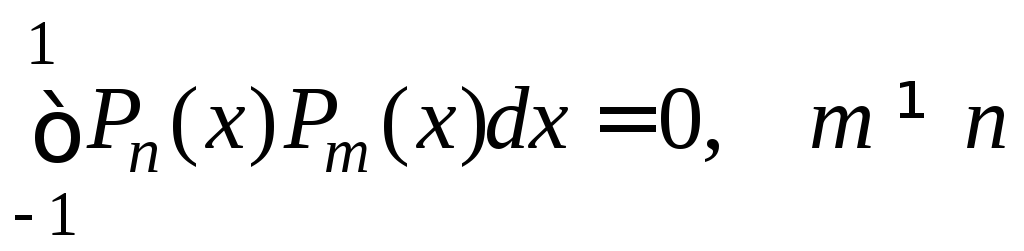 .
.
При
![]() решениями уравнения (20) будут присоединённые
функции Лежандра первого рода
решениями уравнения (20) будут присоединённые
функции Лежандра первого рода
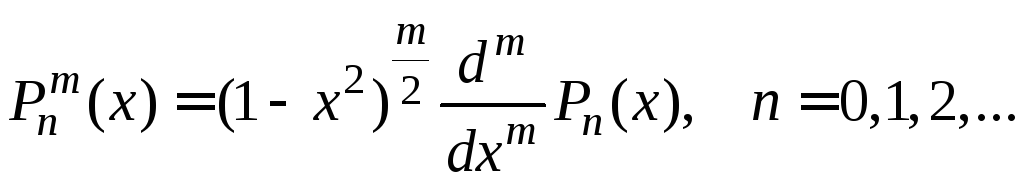
Функции
Лежандра в пространстве
![]() ортогональны с весом
ортогональны с весом
![]() ,
то есть
,
то есть
 .
.
Решения дифференциального уравнения
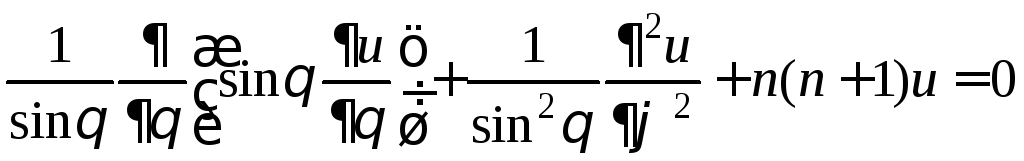 ,
,
получаемого при решении уравнения Лапласа по методу Фурье в сферических координатах, называются сферическими функциями и определяются формулой
![]() .
.
Здесь![]() .
.
Сферические
функции в пространстве
![]() ортогональны с весом
ортогональны с весом
![]() ,
то есть
,
то есть
 .
.
4.2.6. Схема метода Фурье
Сущность
метода разделения переменных заключается
в следующем. Неизвестная функция
![]() ,
зависящая от
,
зависящая от
![]() и
и
![]() ,
заменяется произведением функций,
каждая из которых зависит только от
,
заменяется произведением функций,
каждая из которых зависит только от
![]() и только от
и только от
![]()
![]() .
.
Это позволяет уравнение с частными производными разделить на несколько дифференциальных уравнений, некоторые из которых вместе с граничными условиями образуют краевую задачу на собственные значения для оператора Лапласа (или какого-либо другого дифференциального оператора)
![]() ,
,
![]() ,
(22)
,
(22)
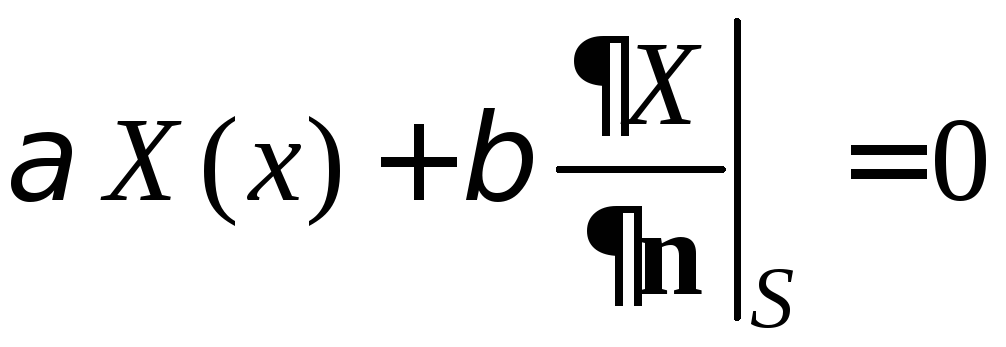 , (23)
, (23)
![]() ,
,
![]() ,
,
![]() +
+![]() >
0,
>
0,
![]() .
.
Значения
параметра
![]() ,
при которых уравнение (22) имеет ненулевые
решения, называются собственными
значениями оператора
,
при которых уравнение (22) имеет ненулевые
решения, называются собственными
значениями оператора ![]() ,
а соответствующие
им решения задачи (22) – (23) называются
собственными функциями оператора
,
а соответствующие
им решения задачи (22) – (23) называются
собственными функциями оператора
![]() .
.
Краевая
задача на собственные значения (22) –
(23) при
![]() называется
задачей Штурма - Лиувилля. Собственные
функции и собственные значения задачи
Штурма - Лиувилля
обладают следующими свойствами:
называется
задачей Штурма - Лиувилля. Собственные
функции и собственные значения задачи
Штурма - Лиувилля
обладают следующими свойствами:
1. Существует счётное множество собственных значений
![]()
которым соответствуют собственные функции
![]()
2.
Собственные функции в области
![]() ,
отвечающие различным собственным
значениям
,
отвечающие различным собственным
значениям
![]() ,
ортогональны с весом
,
ортогональны с весом
![]()
![]() .
.
После
того как будет решена краевая задача
(22) − (23), то есть будут найдены собственные
значения
![]() и собственные функции
и собственные функции
![]() этой задачи, искомое решение
этой задачи, искомое решение
![]() исходной краевой задачи представляется
в виде рядя Фурье по собственным функциям
исходной краевой задачи представляется
в виде рядя Фурье по собственным функциям
![]()
![]() .
.
Неизвестные
коэффициенты
![]() находят с помощью начальных или граничных
условий краевой задачи.
находят с помощью начальных или граничных
условий краевой задачи.
Если
полученный ряд допускает почленное
дифференцирование по переменным
![]() и
и
![]() два раза, то есть ряд после двукратного
дифференцирования по переменным
два раза, то есть ряд после двукратного
дифференцирования по переменным
![]() и
и
![]() сходится в области
сходится в области
![]() равномерно, то этот ряд будет решением
краевой задачи в области
равномерно, то этот ряд будет решением
краевой задачи в области
![]() .
В тех случаях, когда указанные условия
не выполняются, можно ограничиться
условием сходимости в среднем. Если же
не удаётся установить выполнение ни
одного из указанных условий, то будем
считать полученное решение формальным.
Более детальное изложение метода Фурье
рассмотрим на примере решения конкретных
краевых задач для уравнений гиперболического,
параболического и эллиптического типа.
.
В тех случаях, когда указанные условия
не выполняются, можно ограничиться
условием сходимости в среднем. Если же
не удаётся установить выполнение ни
одного из указанных условий, то будем
считать полученное решение формальным.
Более детальное изложение метода Фурье
рассмотрим на примере решения конкретных
краевых задач для уравнений гиперболического,
параболического и эллиптического типа.
