4. Методы решения задач для уравнений с частными производными
Наиболее распространёнными методами решения задач для уравнений с частными производными являются метод характеристик, метод разделения переменных и метод интегральных преобразований.
4.1. Метод характеристик
Основой метода характеристик является приведение уравнения к каноническому виду с помощью невырожденной замены независимых переменных. В качестве новых независимых переменных используются характеристики уравнения. В результате такой замены заданное уравнение сводится к более простому виду, что в ряде случаев позволяет найти решение задачи в квадратурах.
4.1.1. Метод Даламбера
Чаще всего метод характеристик применяется к решению задач для волнового уравнения и называется в этом случае методом Даламбера.
Пример 6. Найдите решение задачи Коши для однородного волнового уравнения на прямой
,
,
,
, 
,
где
,
.
Решение. Эту задачу можно рассматривать, как математическую модель малых колебаний бесконечной струны. Приводим уравнение к каноническому виду
,
.
Как видим, оно совпадает с уравнением (8), общее решение которого определяется формулой (9)
или в прежних переменных
. (11)
Функция
с ростом
смещается по оси
без изменения своей формы вправо, а
функция
–
влево. Поэтому функцию
называют прямой (правой) волной, а функцию
− обратной (левой) волной. Значит, общее
решение волнового уравнения представляет
собой суперпозицию двух расходящихся
волн.
Для нахождения решения задачи Коши подставим полученное общее решение в начальные условия
,
(12)
.
Проинтегрируем
последнее равенство по переменной
.
(13)
Здесь
и
– константы. Выражения (12) и (13) образуют
систему линейных алгебраических
уравнений относительно функций
и
.
Определитель этой системы
.
Поэтому система имеет единственное
решение
(14)
Подставляем (14) в (11) и получаем решение задачи Коши для однородного волнового уравнения на прямой (формула Даламбера)
.
(15)
Замечание.
Как следует
из формулировки задачи Коши, функция
должна быть дифференцируемая, а функция
− дважды дифференцируемая. Несмотря
на это, в предлагаемых задачах будут
рассматриваться функции
с точками разрыва первого рода
(кусочно-непрерывные функции), а функции
− с угловыми точками (кусочно-гладкие
функции). Это объясняется тем фактом,
что с помощью незначительных изменений
функции
и
можно сделать достаточно гладкими, а
полученные для этих сглаженных функций
решения
будут
мало отличаться от
.
Пример 7. Используя формулу Даламбера, найдите решение задачи Коши (задание 5)
,
,
, 
.
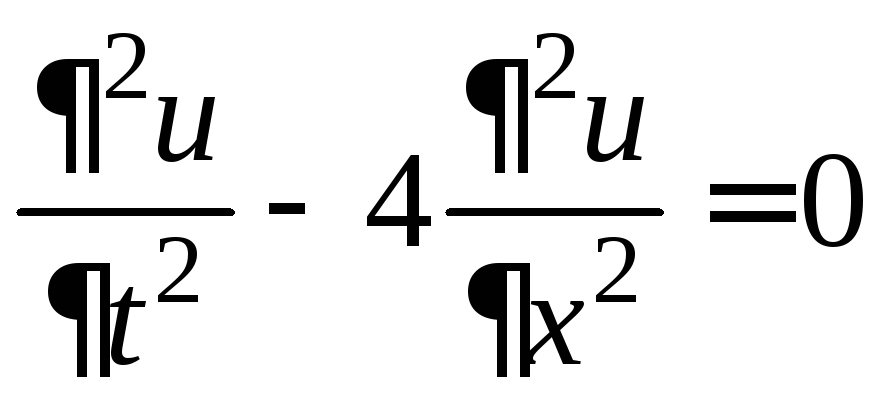Решение.
Подставим
в формулу Даламбера значения функций
и
и получим искомое решение
.
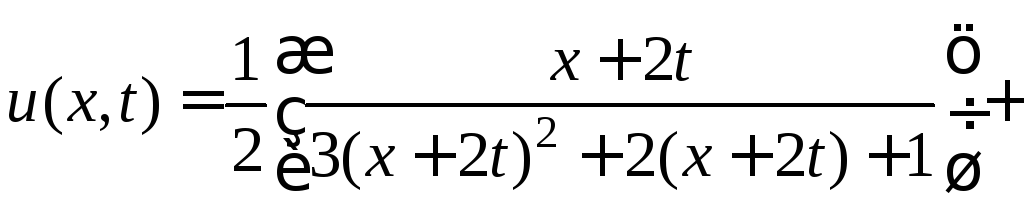
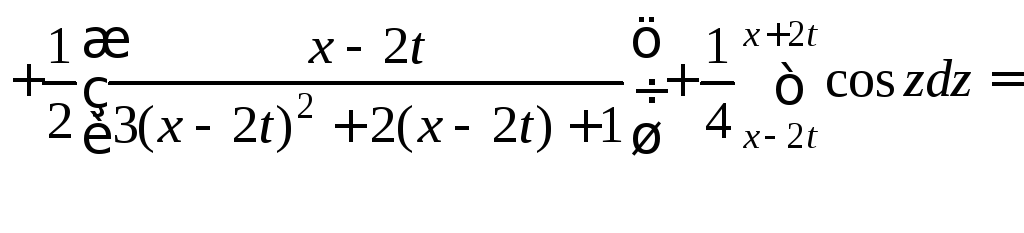
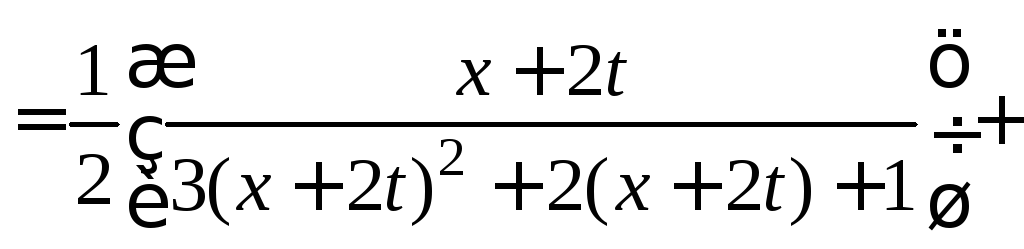
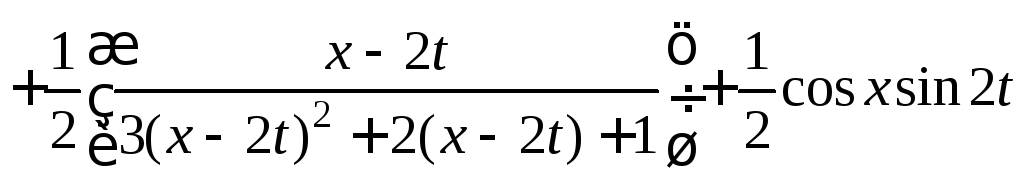Пример 8. Используя формулу Даламбера, найдите решение смешанной задачи для однородного волнового уравнения на полупрямой (задание 6)
,
,
,
, 
,
.
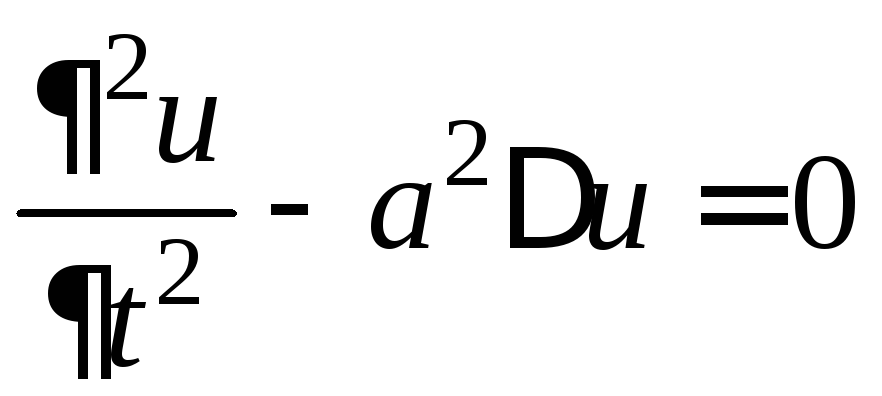Решение.
Эту задачу
можно рассматривать как задачу о малых
колебаниях полубесконечной струны.
Кроме начальных условий, необходимо
ещё задать граничное условие, например,
в точке
Для закреплённой в точке
струны это будет граничное условие
первого рода
,
для
свободного конца в точке
− граничное условие второго рода
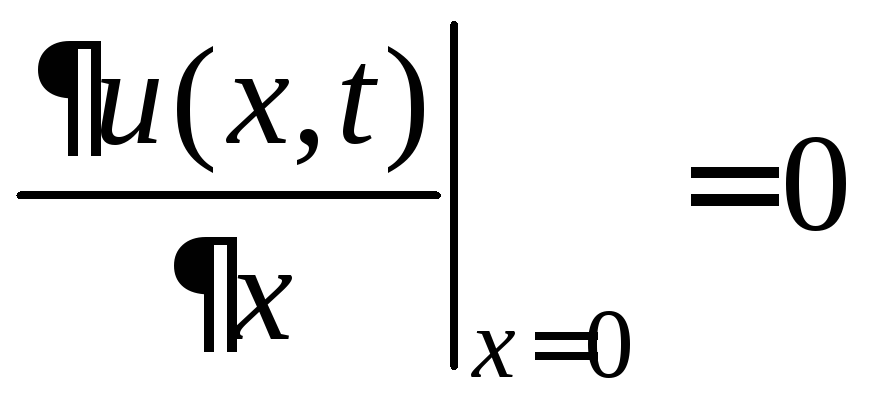
и
для упругого закрепления в точке
− граничное условие третьего рода
.
По
условию задачи функции
,
и
определены лишь при
.
Доопределим их при
,
полагая
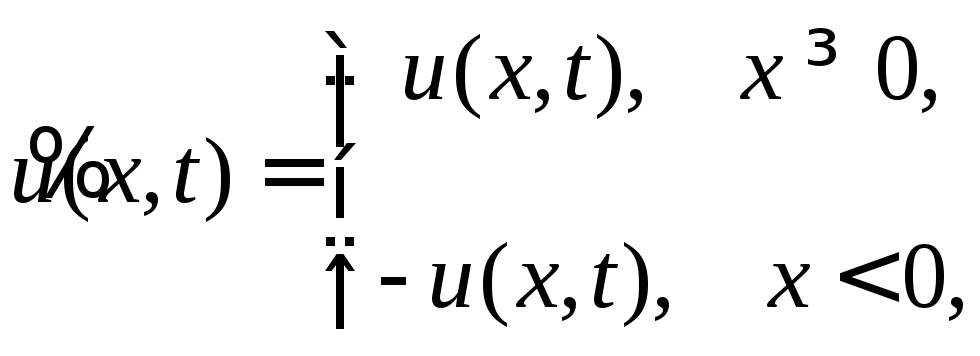
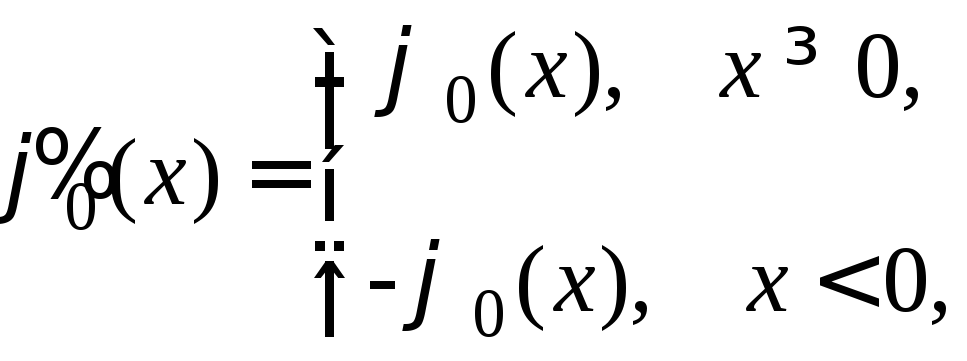
Теперь
функции
,
и
определены на всей числовой прямой.
Проверяем выполнение условия согласования
,
.
Полученную
задачу для функции
можно рассматривать, как задачу Коши,
решение которой определяется формулой
Даламбера
.
Подставим
в полученное выражение значения функций
и
,
ограничившись интересующим нас условием
исходной задачи
,
и получим искомое решение
