2. Характеристические поверхности (характеристики) квазилинейного уравнения второго порядка. Приведение квазилинейного уравнения второго порядка к каноническому виду

Обыкновенное дифференциальное уравнение

. (4)

называется характеристическим уравнением для уравнения (2). Если – общие интегралы уравнения (4), то функции называются характеристиками уравнения (2). Характеристики используются для приведения уравнения к каноническому виду (метод характеристик). Уравнение (4) эквивалентно двум уравнениям

, (5)

, (6)

.

Для уравнения эллиптического типа общие интегралы уравнений (5) и (6) будут комплексно-сопряжёнными

,

.

С помощью замены и уравнение (2) приводится к каноническому виду

.

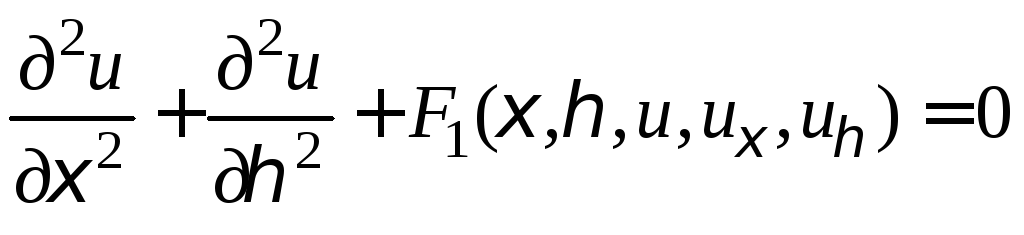Для уравнения гиперболического типа общие интегралы уравнений (5) и (6) будут вещественны и различны. Замена и приводит уравнение (2) к каноническому виду

.

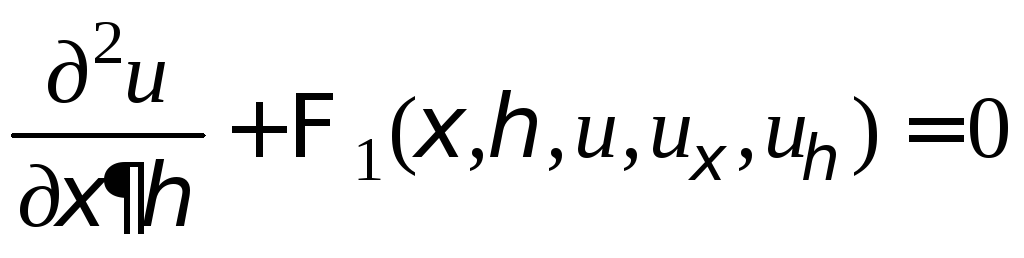После замены переменных и полученное уравнение в новых переменных принимает вид

.

Это вторая каноническая форма для гиперболического уравнения.

Если уравнение (2) принадлежит к параболическому типу, то общие интегралы уравнения (4) совпадают, то есть

.

Положим , а выберем независимо от , так чтобы преобразование было невырожденным. Уравнение (2) в рассматриваемой области приводится к каноническому виду

.

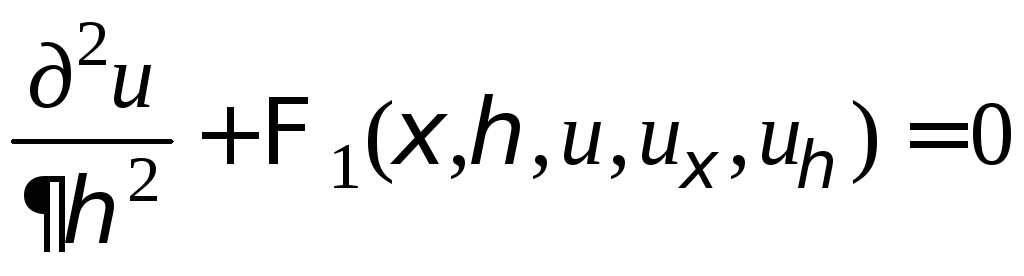Пример 3. Приведите к каноническому виду уравнения (задание 3):

а),

б),

в).

Решение. а) Здесь ,,– коэффициенты уравнения. Тогда определитель. Значит это уравнение эллиптического типа. Его уравнение характеристик:

или

,

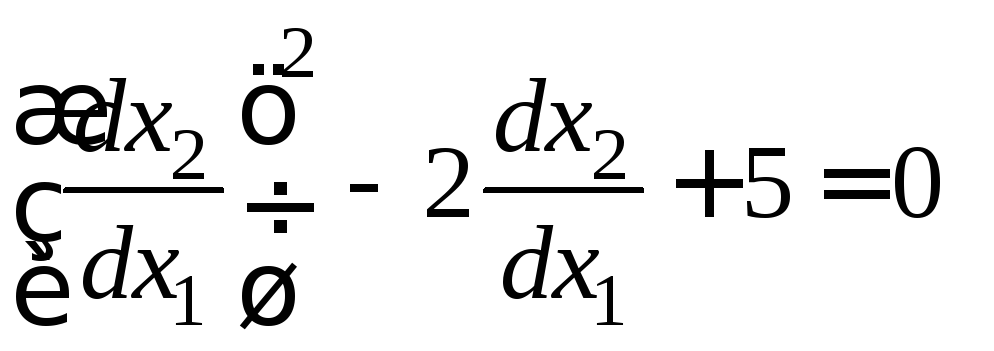откуда

,

то есть иии. Выберем в качестве новых переменныхи, тогда

, ,

, ,.

В новых переменных уравнение

имеет вид

или

.

б) Здесь – коэффициенты уравнения. Тогда. Значит это уравнение гиперболического типаc уравнением характеристик

или

,

откуда

,

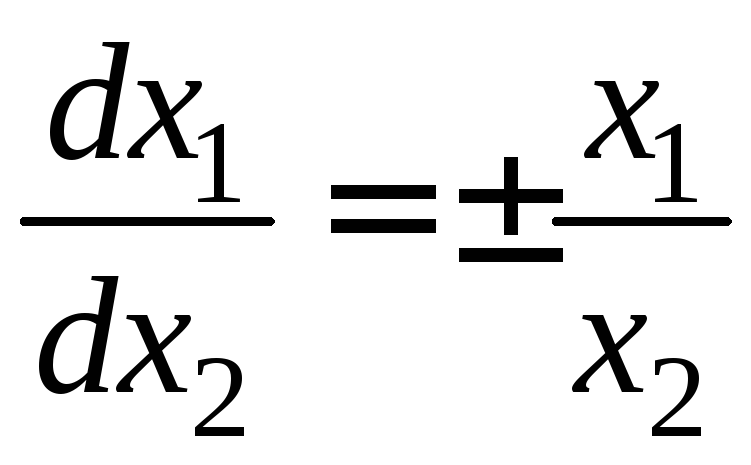то есть

и и.

За новые переменные выберем и,, (так как по условию). В этих переменных

, ,

,

.

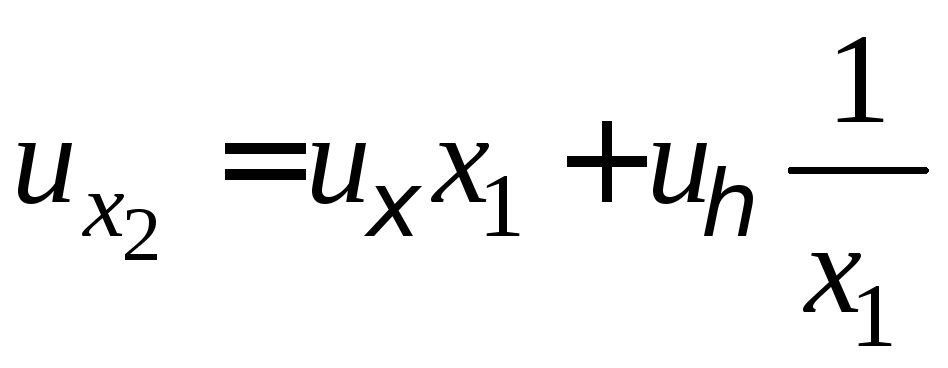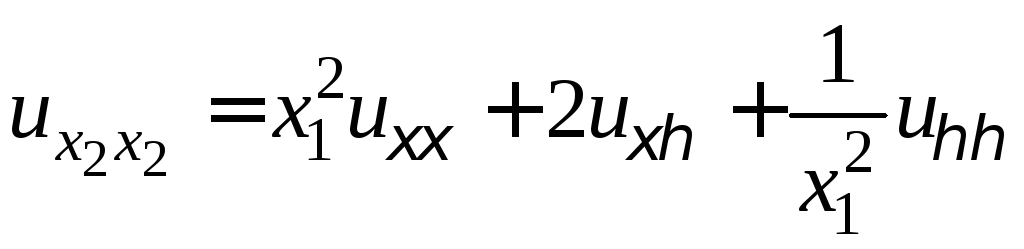После подстановки найденных значений производных в исходное уравнение получаем

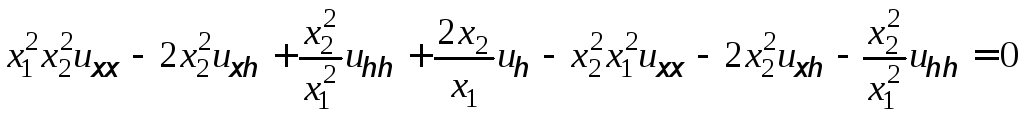
или

.

В этом уравнении нужно ещё заменить и с помощью формул

,

что позволяет привести его к каноническому виду

.

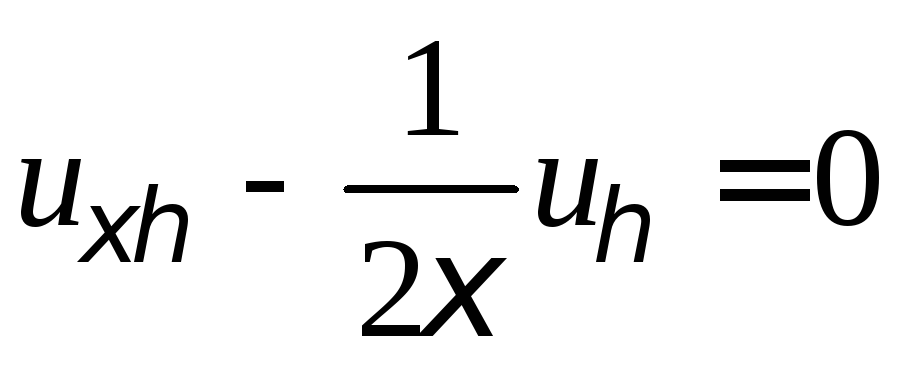Наконец, с помощью замены

получаем вторую каноническую форму

.

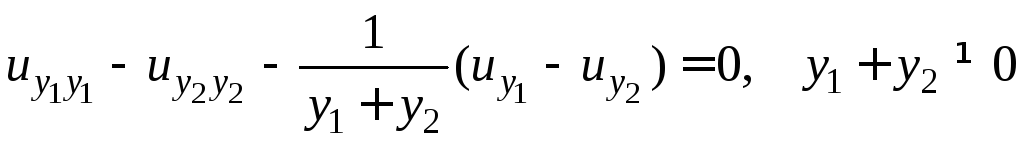в) Коэффициенты уравнения равны . Так как определитель, то это уравнение параболического типаc уравнением характеристик

или

,

откуда . Положим, авыберем независимо от, например,. В этих переменных

, ,,

,.

После подстановки найденных значений производных в исходное уравнение получаем

или

.

Замечание. В случае уравнения с постоянными коэффициентами после приведения этого уравнения к каноническому виду можно добиться дальнейшего упрощения с помощью замены

, (7)

где постоянные и подбираются таким образом, чтобы коэффициенты при и в эллиптическом и гиперболическом уравнениях и коэффициент при или при , а также коэффициент при в параболическом уравнении обращались бы в нуль.

Пример 4. Упростите уравнения:

а),

б) .

Решение. а) Заменяем функцию на по формуле (7)

.

Пр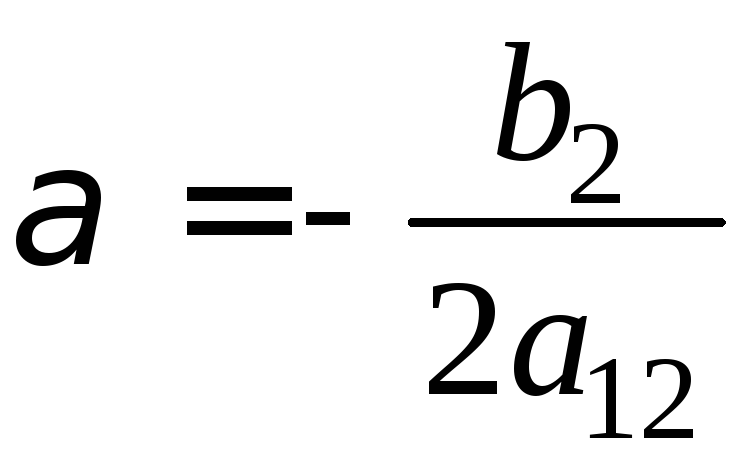и и 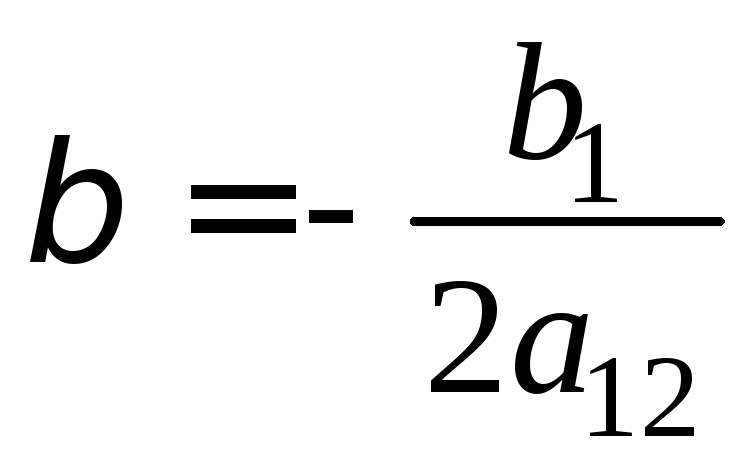получаем

.

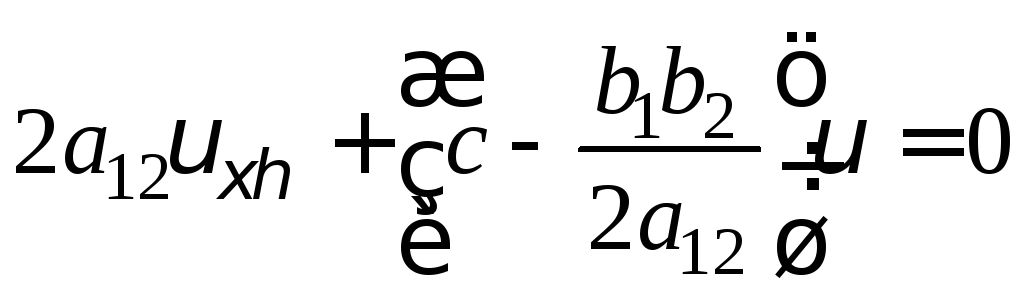б) Подставляем (7) в заданное уравнение и получаем

.

При , имеем

.

Иногда после приведения уравнения к каноническому виду удаётся найти его общее решение.