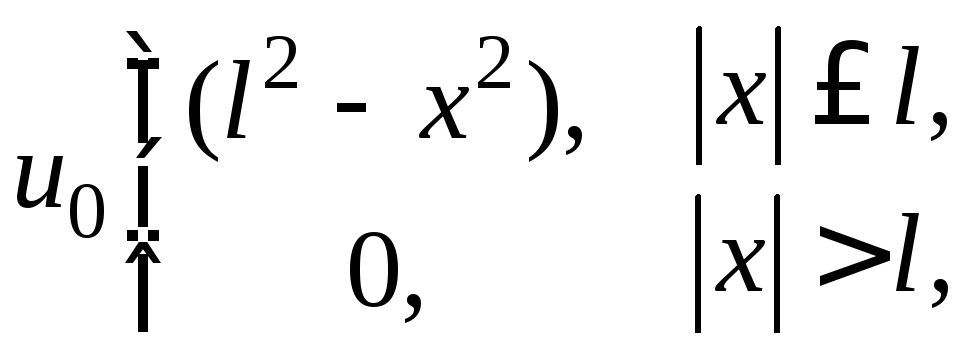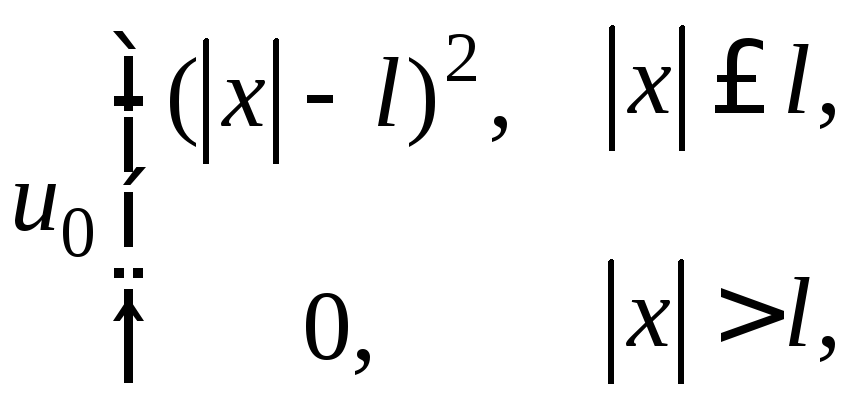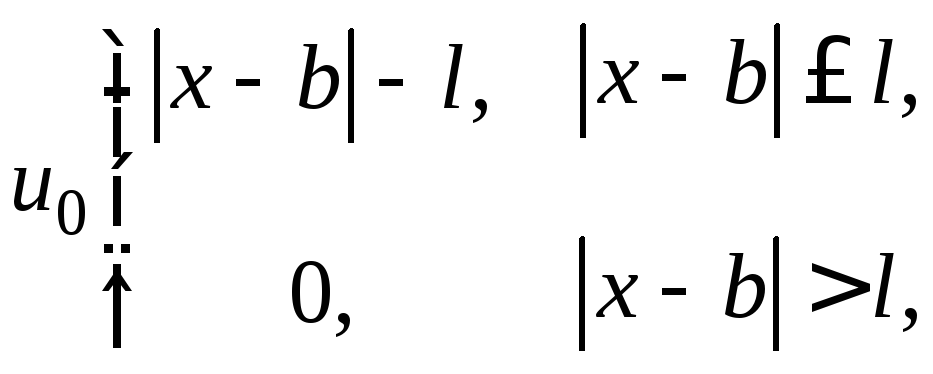- •II. Уравнения математической физики
- •1. Определение и классификация дифференциальных уравнений с частными производными
- •2. Характеристические поверхности (характеристики) квазилинейного уравнения второго порядка. Приведение квазилинейного уравнения второго порядка к каноническому виду
- •Пример 3. Приведите к каноническому виду уравнения (задание 3):
- •Пример 4. Упростите уравнения:
- •Пример 5. Найдите общее решение уравнения (задание 4)
- •3. Основные уравнения с частными производными. Задачи для уравнений с частными производными
- •4. Методы решения задач для уравнений с частными производными
- •4.1. Метод характеристик
- •4.1.1. Метод Даламбера
- •Пример 6. Найдите решение задачи Коши для однородного волнового уравнения на прямой
- •4.1.2. Фазовая плоскость
- •Вариант первый
- •Решение задачи находится по формуле Даламбера
- •Вариант второй
- •4.2. Метод разделения переменных (метод Фурье)
- •4.2.1. Ортогональные системы
- •4.2.2. Функции Бесселя
- •4.2.3. Модифицированные функции Бесселя
- •4.2.4. Сферические функции Бесселя
- •4.2.5. Шаровые и сферические функции
- •4.2.6. Схема метода Фурье
- •Пример 10. Найдите решения задачи Штурма - Лиувилля (задание 8)
- •Пример 11. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в круге
- •Пример 12. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в прямоугольнике (задание 9)
- •Пример 13. Найдите решение краевой задачи для уравнения Лапласа в круге (задание 11)
- •Пример 14. Найдите решение краевой задачи для уравнения Лапласа в прямоугольнике (задание 10)
- •Вариант первый
- •Вариант второй
- •Вариант третий
- •Пример 15. Найдите решение краевой задачи для уравнения Лапласа в шаре (задание 12)
- •Вариант третий
- •Пример 16. Найдите решение краевой задачи для уравнения Лапласа в цилиндре (задание 13)
- •Пример 17. Найдите решение краевой задачи для уравнения Пуассона в кольце (задание 14)
- •Пример 18. Найдите решение краевой задачи для уравнения Гельмгольца в круге (задание 15)
- •Имеем краевую задачу третьего рода
- •Пример 19. Найдите решение краевой задачи для уравнения Гельмгольца в шаре (задание 16)
- •Пример 21. Найдите решение смешанной задачи для однородного волнового уравнения в интервале (см. Задание17)
- •Пример 22. Найдите решение смешанной задачи для однородного волнового уравнения в прямоугольнике (задание 18)
4.1.2. Фазовая плоскость
Свойства решения волнового уравнения
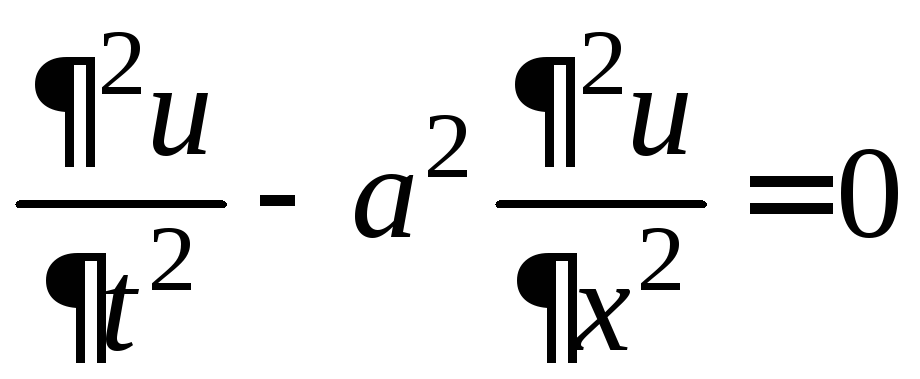
удобно
исследовать с помощью фазовой плоскости
![]() ,
которая называется также плоскостью
состояний. Характеристиками волнового
уравнения являются прямые
,
которая называется также плоскостью
состояний. Характеристиками волнового
уравнения являются прямые
![]() и
и
![]() .
Функция
.
Функция
![]() сохраняет постоянное значение вдоль
характеристики
сохраняет постоянное значение вдоль
характеристики
![]() ,
а функция
,
а функция
![]() – вдоль характеристики
– вдоль характеристики
![]() .
Пусть функции
.
Пусть функции
![]() и
и
![]() отличны от нуля в интервале
отличны от нуля в интервале
![]() и равны нулю вне этого интервала.
и равны нулю вне этого интервала.

Рис. 4.1
Проведем
через точки
![]() и
и
![]() характеристики
характеристики
![]() ,
,
![]() для функции
для функции
![]() и
и
![]() ,
,
![]() для функции
для функции
![]() (рис.4.1). Они разбивают фазовую плоскость
на шесть областей. На интервале
(рис.4.1). Они разбивают фазовую плоскость
на шесть областей. На интервале
![]() задано начальное возмущение для этих
функций
задано начальное возмущение для этих
функций
![]() .
.
При
![]() ,
то есть с ростом
,
то есть с ростом
![]() начальное возмущение функции
начальное возмущение функции
![]() будет перемещаться в полосе, ограниченной
прямыми
будет перемещаться в полосе, ограниченной
прямыми
![]() ,
,
![]() (области VI
и IV).
Поэтому функция
(области VI
и IV).
Поэтому функция
![]() ,
где
,
где
![]() ,
будет отличной от нуля только в областях
VI
и IV.
В областях же I,
II,
III
и V
,
будет отличной от нуля только в областях
VI
и IV.
В областях же I,
II,
III
и V
![]() .
Начальное возмущение функции
.
Начальное возмущение функции
![]() будет перемещаться в полосе, ограниченной
прямыми
будет перемещаться в полосе, ограниченной
прямыми
![]() ,
,
![]() (области VI
и II),
а функция
(области VI
и II),
а функция
![]() ,
где
,
где
![]() ,
будет отлична от нуля в областях VI
и II,
а в областях I,
III,
IV
и V
,
будет отлична от нуля в областях VI
и II,
а в областях I,
III,
IV
и V
![]() .
Таким образом, состояние процесса в
любой точке
.
Таким образом, состояние процесса в
любой точке
![]() фазовой плоскости зависит от того, в
какой из этих областей находится эта
точка. Так в областях I,
III,
V
отклонение равно нулю. В области II
отклонение вызывается только правой
волной, в области IV
– только левой волной, а в области VI
– и левой, и правой волной вместе.
фазовой плоскости зависит от того, в
какой из этих областей находится эта
точка. Так в областях I,
III,
V
отклонение равно нулю. В области II
отклонение вызывается только правой
волной, в области IV
– только левой волной, а в области VI
– и левой, и правой волной вместе.
Пример 9. Неограниченная
струна имеет на отрезке
![]() локальное начальное отклонение
локальное начальное отклонение
![]() и локальную начальную скорость
и локальную начальную скорость
![]() .
Найдите формулы, определяющие профиль
струны при
.
Найдите формулы, определяющие профиль
струны при
![]() (задание 7).
(задание 7).
|
№ |
|
|
|
|
1 |
9 |
|
0 |
|
2 |
4 |
|
0 |
|
3 |
1 |
0 |
|
Решение. Данная задача представляет собой задачу Коши для однородного волнового уравнения на прямой. Рассмотрим предложенные варианты задачи.
Вариант первый
|
№ |
|
|
|
|
1 |
9 |
|
0 |
Имеем задачу Коши
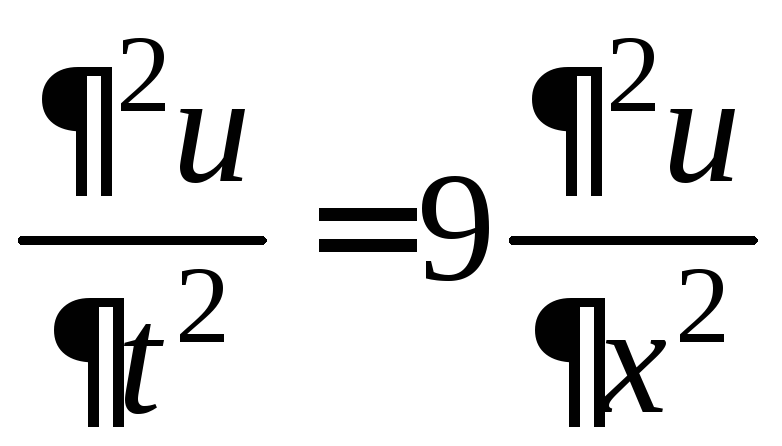 ,
,
![]() ,
,
![]() ,
,
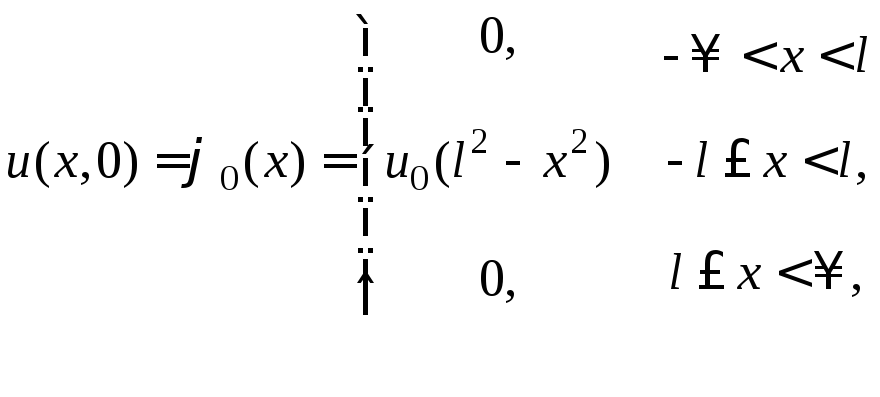
![]() ,
,![]() .
.
Её можно истолковать как математическую модель свободных колебаний бесконечной струны, которая в начальный момент времени имела начальное отклонение в форме квадратичной параболы (рис. 4.2) и начальную скорость, равную нулю.

Решение задачи находится по формуле Даламбера
 .
.
В
рассматриваемом случае
![]() ,
поэтому её решение будет иметь вид
,
поэтому её решение будет иметь вид
![]() .
.
Для
получения формул, определяющих форму
струны при
![]() ,
рассмотрим разбиение фазовой плоскости
,
рассмотрим разбиение фазовой плоскости
![]() характеристиками волнового уравнения,
проведенными из концов интервала (–l,
l).
На этом интервале, согласно начальному
условию
характеристиками волнового уравнения,
проведенными из концов интервала (–l,
l).
На этом интервале, согласно начальному
условию
![]() ,
отклонение отлично от нуля (рис. 4.3).
Из рисунка видно, что при
,
отклонение отлично от нуля (рис. 4.3).
Из рисунка видно, что при
![]() достаточно ограничиться двумя характерными
случаями:
достаточно ограничиться двумя характерными
случаями:
![]() и
и
![]() .
.
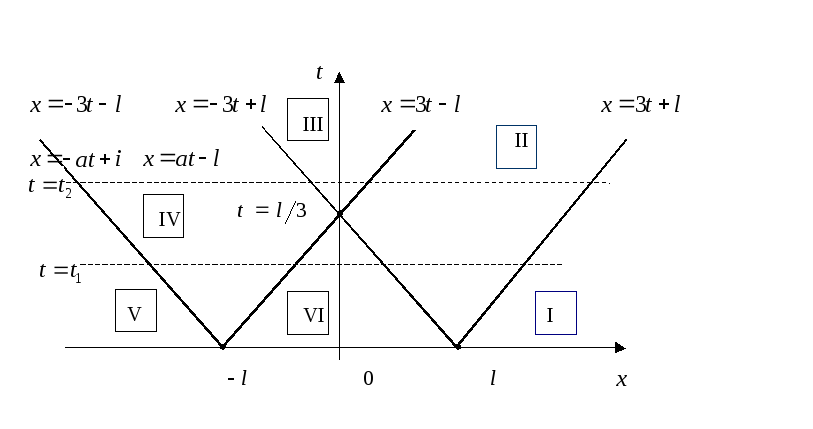 Рис.
4.3
Рис.
4.3
Точка
![]() представляет собой точку пересечения
прямых
представляет собой точку пересечения
прямых
![]() и
и
![]() .
Рассмотрим каждый из этих случаев в
отдельности.
.
Рассмотрим каждый из этих случаев в
отдельности.
а)
Пусть
![]() ,
,
![]() .
Тогда при перемещении вдоль прямой
.
Тогда при перемещении вдоль прямой
![]() слева направо точка
слева направо точка
![]() фазовой плоскости последовательно
проходит области V, IV, VI, II, I. Профиль
струны в этом случае описывается
соотношениями
фазовой плоскости последовательно
проходит области V, IV, VI, II, I. Профиль
струны в этом случае описывается
соотношениями

б)
![]() ,
,
![]() .
При перемещении вдоль прямой
.
При перемещении вдоль прямой
![]() слева направо точка
слева направо точка
![]() фазовой плоскости последовательно
проходит области V, IV, III,
II, I и профиль струны будет задаваться
соотношениями
фазовой плоскости последовательно
проходит области V, IV, III,
II, I и профиль струны будет задаваться
соотношениями