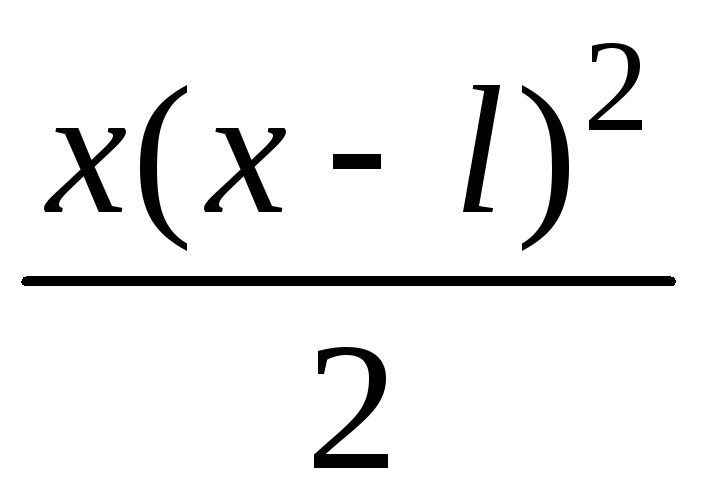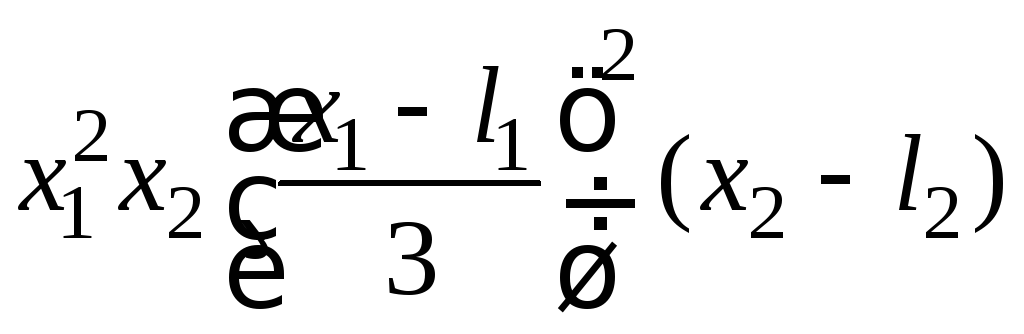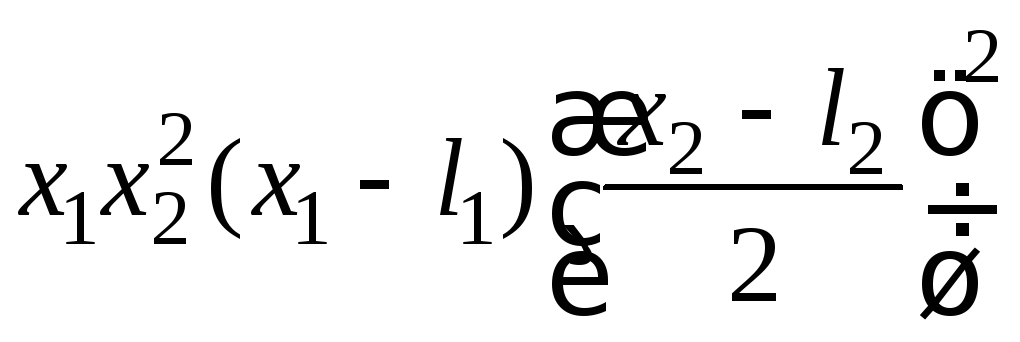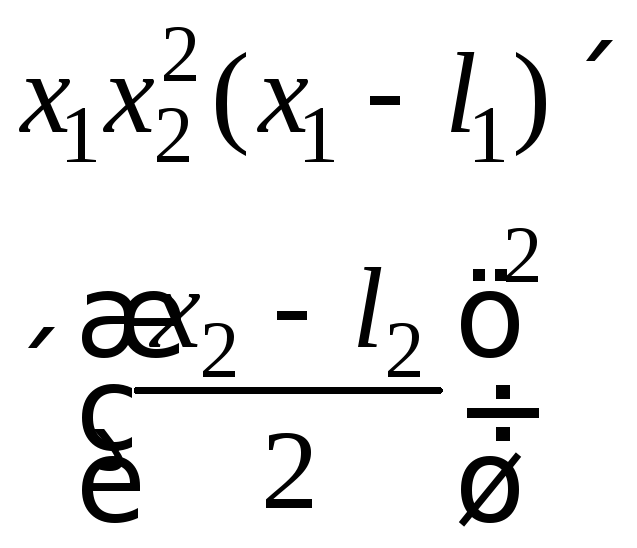Пример 21. Найдите решение смешанной задачи для однородного волнового уравнения в интервале (см. Задание17)
|
№ |
|
|
|
|
|
|
|
|
|
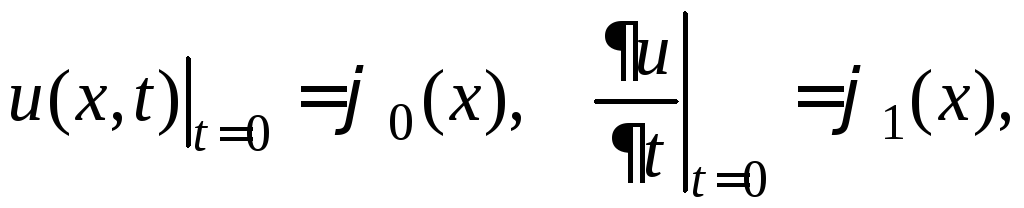
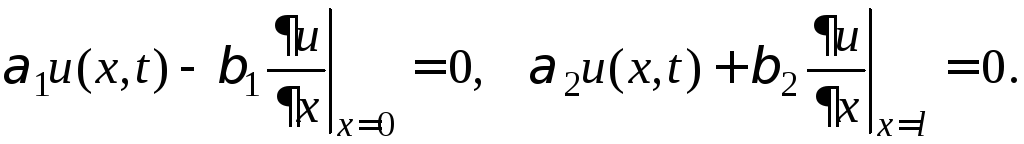
1 |
4 |
3 |
|
0 |
0 |
1 |
0 |
1 |
|
2 |
1 |
2 |
0 |
|
1 |
0 |
0 |
1 |
|
3 |
9 |
1 |
|
|
1 |
1 |
1 |
1 |
Решение. Предложенная задача является частным случаем задачи, рассмотренной в примере 20. Следуя схеме решения этой задачи, составляем краевую задачу на собственные значения для оператора Лапласа. В данном случае это будет задача Штурма - Лиувилля (см. пример 10)
(1)
(2)
с характеристическим уравнением
и решениями в виде
или
.
Рассмотрим конкретные варианты, предложенные в условии задачи.
Вариант первый
|
№ |
|
|
|
|
|
|
|
|
|
1 |
4 |
3 |
|
0 |
0 |
1 |
0 |
1 |
Задача (1) − (2) для этих параметров
будет иметь характеристическое уравнение
.
Корни этого уравнения (собственные значения задачи Штурма -Лиувилля) в данном случае равны
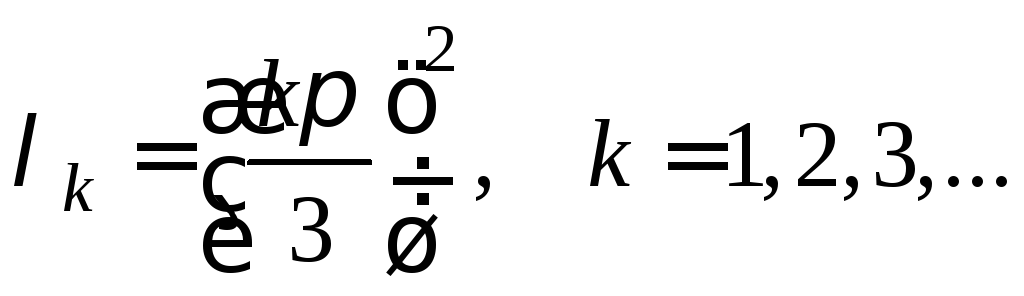
Решения задачи Штурма - Лиувилля (собственные функции) можно представить в виде
.
Подставим
найденные значения для
и заданные значения для
в
выражения (8) − (9) (см. пример 20) и получим
,
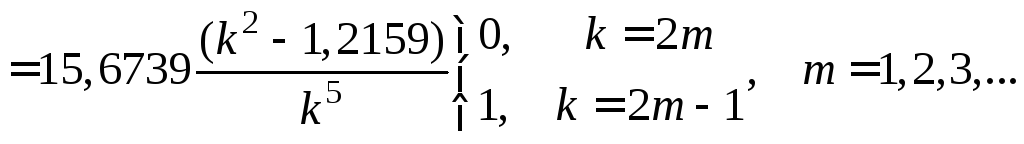
Вариант второй
|
№ |
|
|
|
|
|
|
|
|
|
2 |
1 |
2 |
0 |
|
1 |
0 |
0 |
1 |
Задача Штурма - Лиувилля для этих параметров
будет иметь характеристическое уравнение
,
собственные значения
,
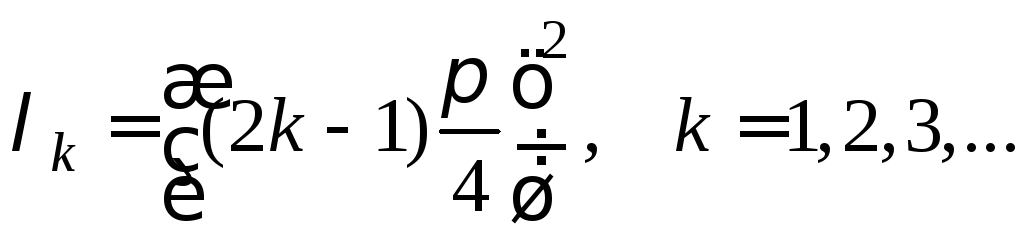собственные функции
.
Подставим
найденные значения для
и заданные значения для
в
выражения (8) − (9) из примера 20 и получим
,
.
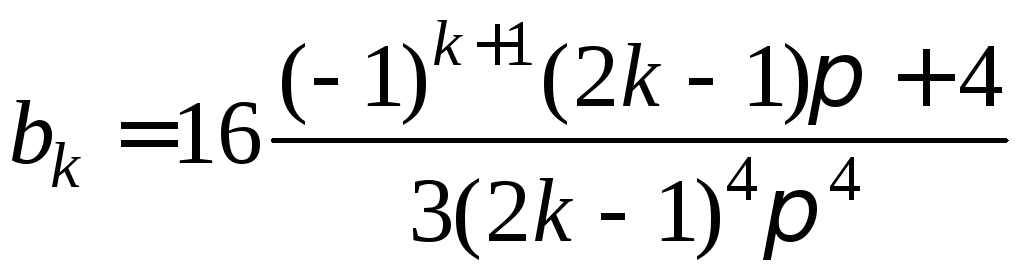
Вариант третий
|
№ |
|
|
|
|
|
|
|
|
|
3 |
9 |
1 |
|
|
1 |
1 |
1 |
1 |
Задача Штурма - Лиувилля для этих параметров
будет иметь характеристическое уравнение
,
первые пять корней которого приведены в таблице
|
|
1 |
2 |
3 |
4 |
5 |
|
|
1,7073 |
13,4924 |
43,3572 |
92,7693 |
161,8809 |
Собственные функции, соответствующие найденным собственным значениям
или
.
С помощью формул
,
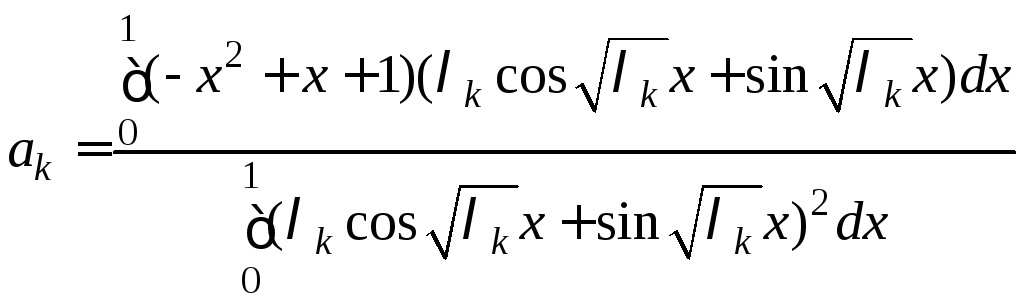находим
коэффициенты
.
Результаты вычислений сводим в таблице
|
|
1 |
2 |
3 |
4 |
5 |
|
|
2,2258 |
0,0651 |
0,0065 |
0,0014 |
0,000460 |
|
|
0,8938 |
0,0056 |
−0,002 |
−0,000699 |
−0,000312 |
Решение
задачи получим после подстановки
найденных значений для
,
в выражение (8) из примера 20
=
+
+
+
+
+…
Пример 22. Найдите решение смешанной задачи для однородного волнового уравнения в прямоугольнике (задание 18)
.
|
№ |
|
|
|
|
|
|
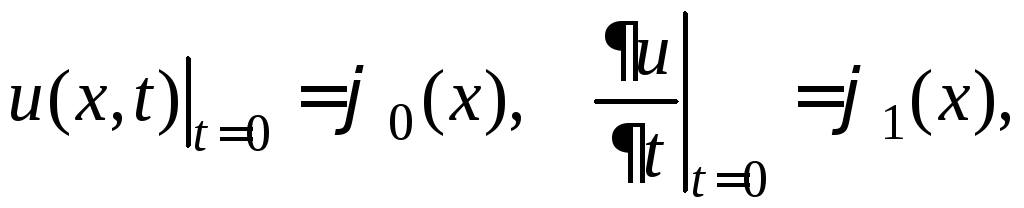
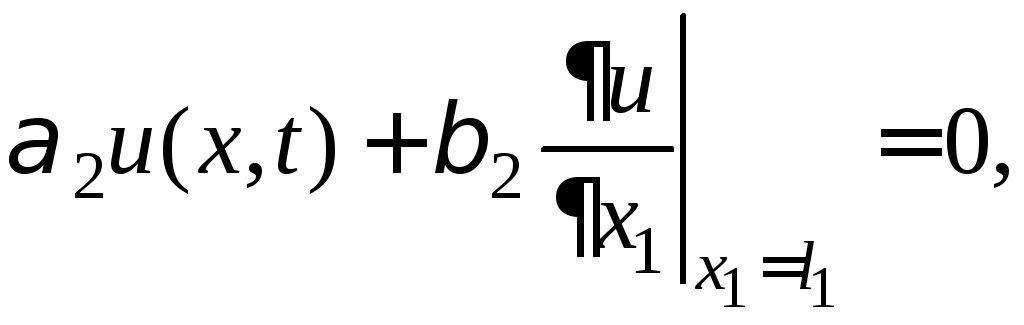
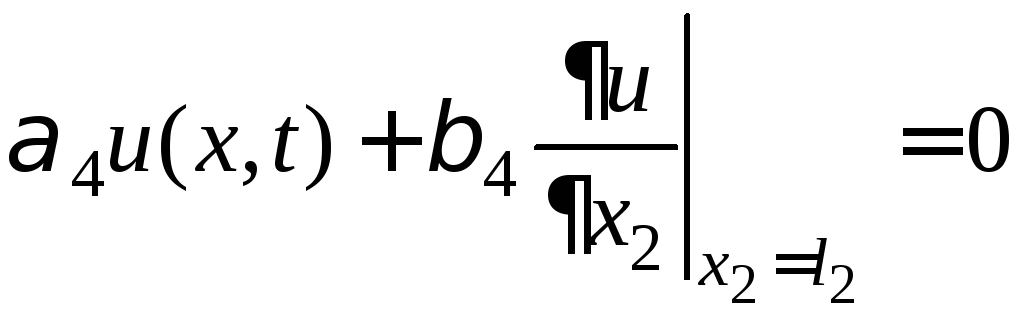1 |
4 |
2 |
4 |
|
0 |
|
2 |
1 |
3 |
5 |
0 |
|
|
3 |
9 |
4 |
6 |
|
0 |
|
№ |
|
|
|
|
|
|
|
|
|
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
|
3 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
Решение. Краевая задача на собственные значения для оператора Лапласа (см. пример 12)
,
(1)
(2)
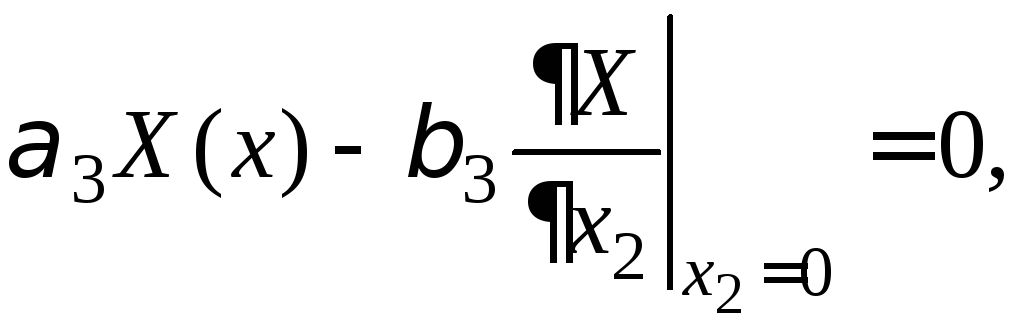
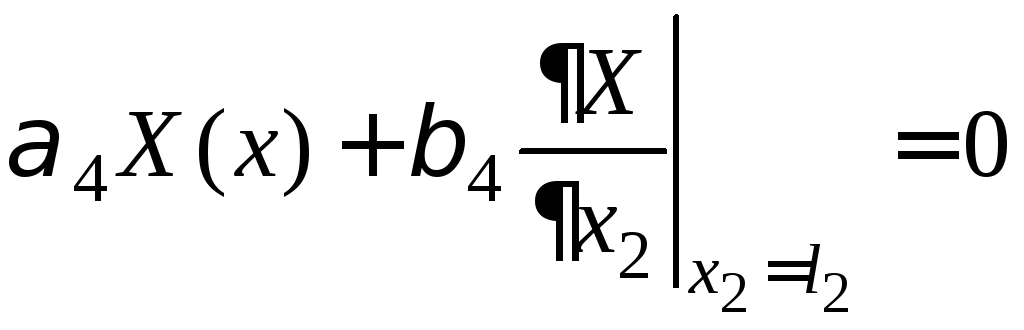(3)
имеет собственные значения и собственные функции, равные соответственно
,
или
или
или
,
(4)
где
и
− корнихарактеристических
уравнений
(5)
и
. (6)
Рассмотрим предложенные варианты краевой задачи.
Вариант первый
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
4 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Характеристические уравнения (5) и (6)
и
имеют корни
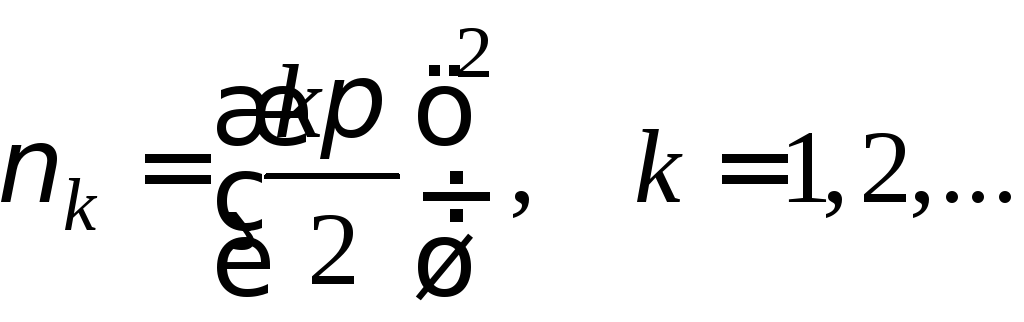
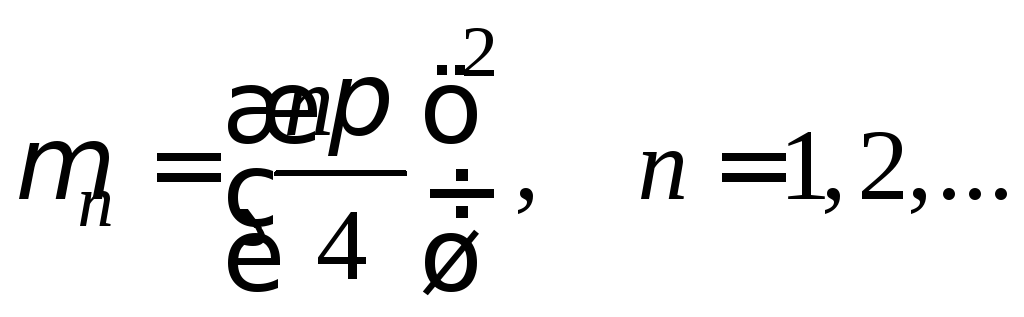
и собственные функции
.
В таком случае собственные значения и собственные функции задачи (1) − (3) будут равны соответственно
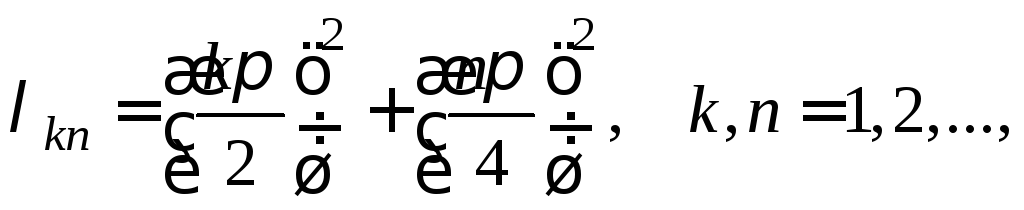
Подставляем
найденные значения для
и заданные значения для
в
выражения (8) − (9) (см. пример 20) и получаем
искомое решение
,
,
.
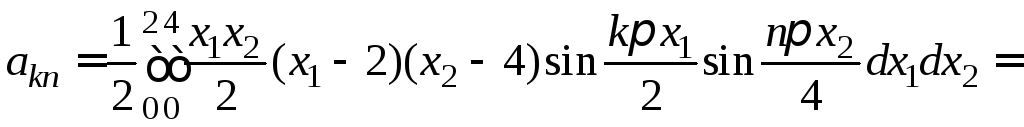
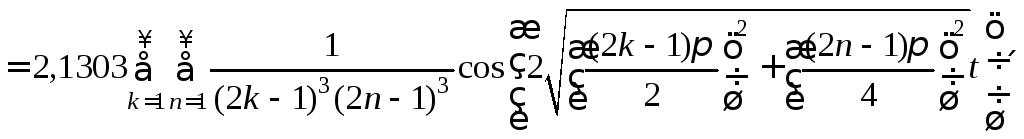
Вариант второй
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
5 |
0 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
В данном случае собственные значения и собственные функции задачи (1) − (3) будут равны соответственно
.
Подставляем
значения для
,
в выражения
(8) − (9) из примера 20 и
получаем
,
.
.
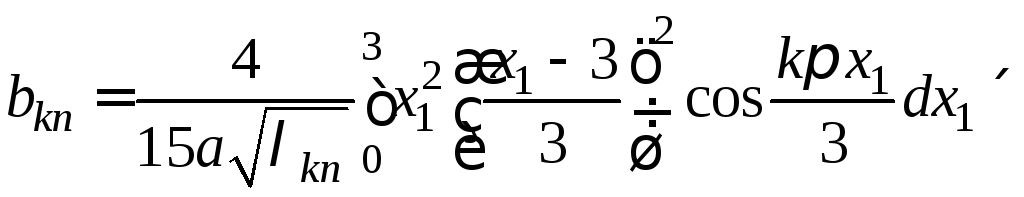
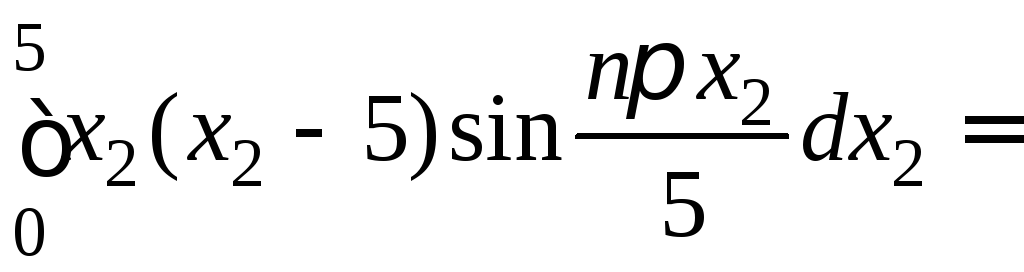
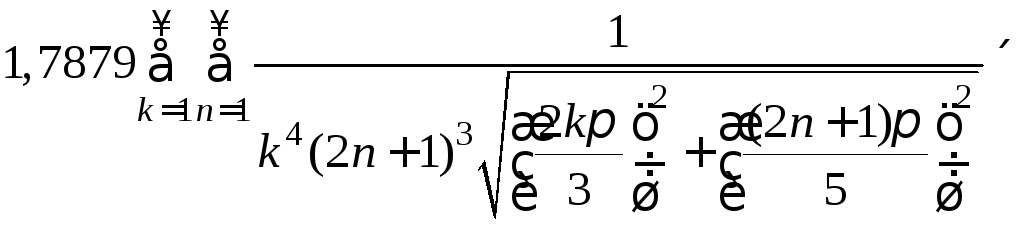
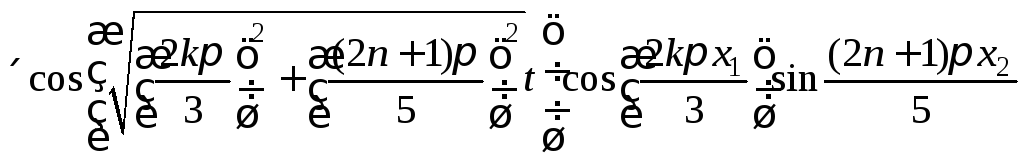Вариант третий
|
|
|
|
|
|
|
|
|
|
|
9 |
4 |
6 |
|
0 |
1 |
0 |
0 |
1 |
Собственные значения и собственные функции задачи (1) − (3) будут равны соответственно
.
Подставляем
значения для
,
в выражения (8) − (9) из примера 20 и получаем
,
,
.
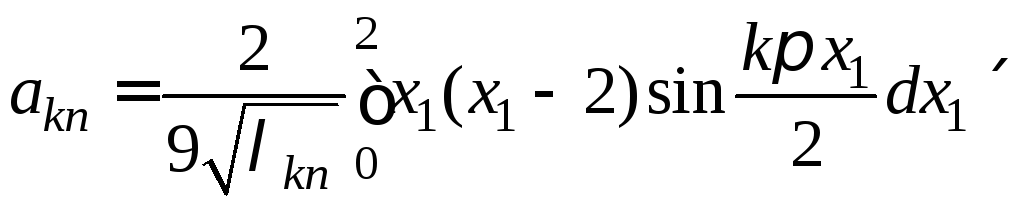
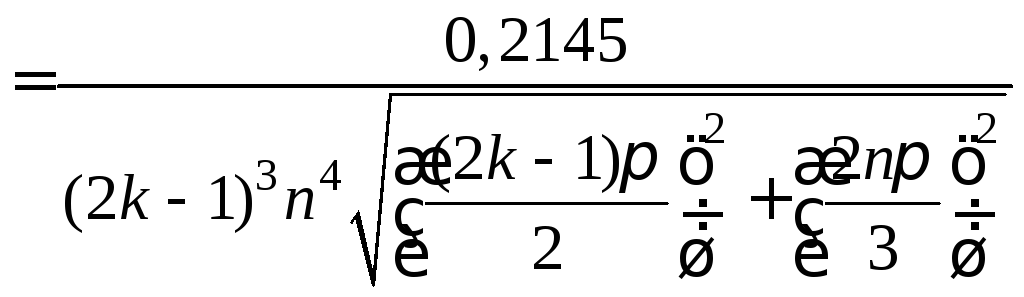
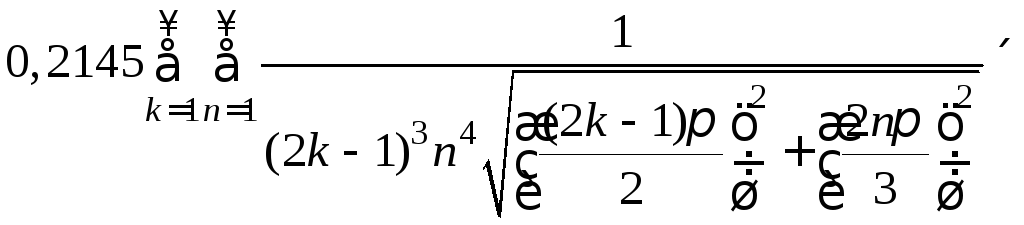
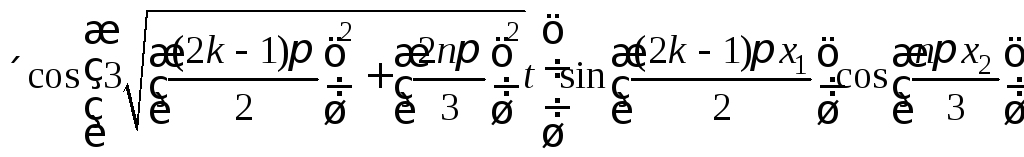