Пример 12. Найдите решения краевой задачи на собственные значения для уравнения Лапласа в прямоугольнике (задание 9)
,
(1)
(2)
.
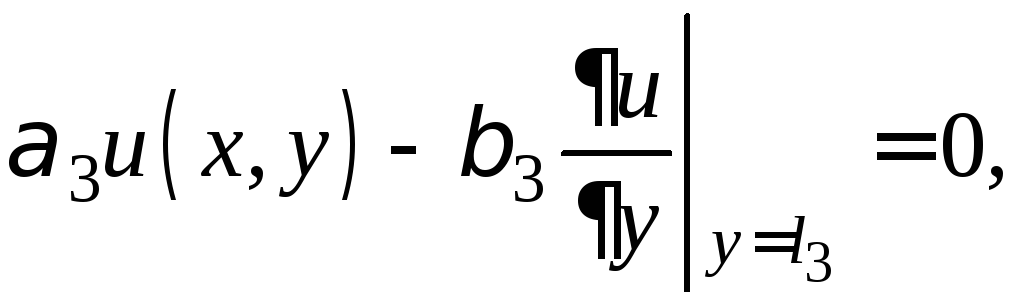
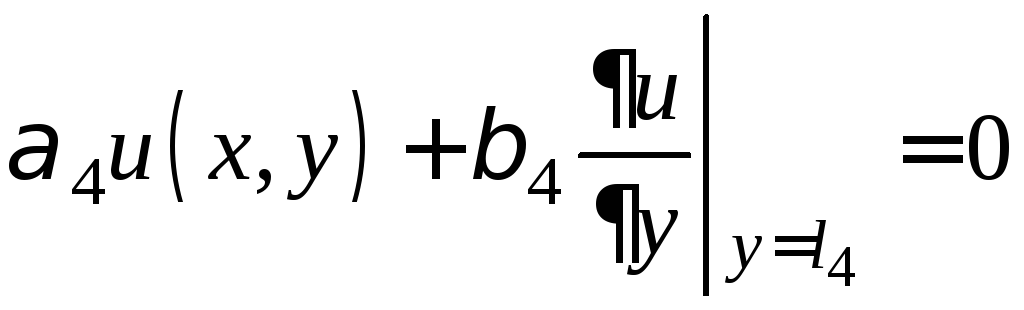(3)
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
1 |
3 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
2 |
1 |
3 |
2 |
5 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
3 |
3 |
5 |
3 |
7 |
1 |
2 |
2 |
3 |
2 |
1 |
1 |
3 |
Решение задачи представим в виде
.
В результате получим
или
после деления этого равенства на 
.
Каждое
из отношений
зависит лишь от одной переменной (от
или
соответственно).
Поэтому такое равенство возможно только
при условии, что эти отношения постоянны.
Положим
.
Тогда с учетом граничных условий получаем две задачи Штурма - Лиувилля:
(4)
(5)
.
Решение задачи Штурма - Лиувилля рассмотрено в примере 10. Для задачи (4) имеем характеристическое уравнение
,
собственные функции
или
.
Для задачи (5) соответственно
и
или
.
Собственные значения и собственные функции задачи (1) − (3) будут равны соответственно
,
или
или
или
.
Рассмотрим предложенные варианты краевой задачи.
Вариант первый
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
1 |
3 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Задача (4) для этих параметров
будет иметь характеристическое уравнение
.
Корни этого уравнения (собственные значения задачи Штурма - Лиувилля) в данном случае равны
Собственные функции
или
.
Аналогично задача (5)
будет иметь характеристическое уравнение
.
Корни этого уравнения (собственные значения задачи Штурма - Лиувилля) равны
Собственные функции
или
.
Собственные значения и собственные функции задачи (1) − (3) будут равны соответственно
,
или
или
или
.
Вариант второй
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
3 |
2 |
5 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
Задача (4) для этих параметров
будет иметь характеристическое уравнение
,
собственные значения
и собственные функции
или
.
Аналогично задача (5)
будет иметь характеристическое уравнение
.
Корни этого уравнения (собственные значения)
Собственные функции
или
.
Собственные значения и собственные функции задачи (1) − (3)
,
или
или
или
.
Вариант третий
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
5 |
3 |
7 |
1 |
2 |
2 |
3 |
2 |
1 |
1 |
3 |
Задача (4) для этих параметров
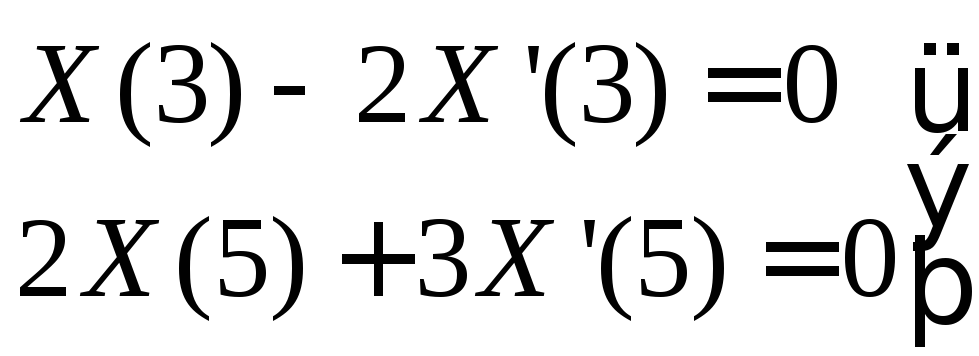
будет иметь характеристическое уравнение
.
Первые пять этого корней уравнения приведены в следующей таблице.
|
|
1 |
2 |
3 |
4 |
5 |
|
|
0,4823 |
3,5055 |
10,9935 |
23,3529 |
40,6333 |
Собственные функции, соответствующие найденным собственным значениям
или
.
Для задачи (5) характеристическое уравнение
.
Первые пять корней этого уравнения приведены в следующей таблице.
|
|
1 |
2 |
3 |
4 |
5 |
|
|
0,2343 |
1,2599 |
3,3264 |
6,5264 |
10,9089 |
Собственные функции, соответствующие найденным собственным значениям
или
.
Собственные значения задачи (37) − (39) будут равны соответственно
|
|
1 |
1 |
1 |
1 |
1 | |||||
|
|
1 |
2 |
3 |
4 |
5 | |||||
|
|
0,2880 |
1,8203 |
11,2978 |
42,8268 |
119,2563 | |||||
|
|
2 |
2 |
2 |
2 |
2 | |||||
|
|
1 |
2 |
3 |
4 |
5 | |||||
|
|
12,3434 |
13,8759 |
23,3535 |
54,8824 |
131,3173 | |||||
|
|
3 |
3 |
3 |
3 |
3 | |||||
|
|
1 |
2 |
3 |
4 |
5 | |||||
|
|
120,9119 |
122,4444 |
131,9220 |
163,4509 |
239,9611 | |||||
|
|
4 |
4 |
4 |
4 |
4 | |||||
|
|
1 |
2 |
3 |
4 |
5 | |||||
|
|
545,4128 |
546,9453 |
556,4229 |
587,9518 |
664,3620 | |||||
|
|
5 |
5 |
5 |
5 |
5 | |||||
|
|
1 |
2 |
3 |
4 |
5 | |||||
|
|
1,6511· |
1,6527· |
1,6621· |
1,6911· |
1,7701· | |||||
Собственные функции задачи (1) − (3)
или
или
или
.