1.1.3. Основной закон радиоактивного распада радионуклида

В результате всех видов радиоактивных превращений количество ядер данного изотопа постепенно уменьшается. Убывание количества распадающихся ядер происходит по экспоненте и записывается в следующем виде:

N=N₀е^-t (1.10)

где N₀ – количество ядер радионуклида в момент начала отсчета времени

(t=0); - постоянная распада, которая для различных радионуклидов разная;N – количество ядер радионуклида спустя времяt; е– основание натурального логарифма (е = 2,713….). Это и есть основной закон радиоактивного распада.

Вывод формулы (1.10.).Естественный радиоактивный распад ядер протекает самопроизвольно, без всякого воздействия из вне. Этот процесс статистический и для отдельно взятого ядра можно лишь указать вероятность распада за определенное время. Поэтому скорость радиоактивного распада можно характеризовать временемt. В практических расчетах для оценки характеристик радиационного излучения используется понятиепериода полураспада Т_1/2. Периодом полураспада называется промежуток времени, в течении которого исходное число радиоактивных ядер уменьшится вдвое, а число распавшихся ядер за время Т_1/2 остается постоянным ( = const).

Пусть имеется число N атомов радионуклида. Тогда, число распадающихся атомов dN за время dt пропорционально числу атомов N и промежутку времени dt:

dN = - lNdt (1.11)

где l - коэффициент пропорциональности, называемый постоянной распада. Знак минус показывает, что числоNисходных атомов уменьшается во времени. Экспериментально показано, что свойства ядер со временем не меняются, от сюда следует, чтоесть величена постоянная. Она носит названиепостоянная распада.Из (1.11) следует, что

 = - =const,

Экспериментально показано, что свойства ядер со временем не меняются, от сюда следует, что есть величена постоянная. Она носит названиепостоянная распада.Из (1.11) следует, что

 = - =const,

В уравнении (1.11.) поделим правую и левую части на Nи проинтегрируем:

dN/N = - ldt (1.12)

N t

∫dN/N = – λ∫ dt (1.13)

N₀ 0

ln N/N₀ = – λt и N = N₀ е^{– λt} , (1.14.)

где N₀ есть начальное число распадающихся атомов (Nприt=0).

В практических расчетах для временной оценки характеристик радиационного излучения используется понятие периода полураспада Т_1/2. Периодом полураспада называется промежуток времени, в течении которого исходное число радиоактивных ядер уменьшится вдвое, а число распавшихся ядер за время Т_1/2 остается постоянным ( = const).

Найдем связь постоянной радиоативного распада с периодом полураспада для чего в уравнении (1.10.) правую и левую часть поделим на N, и приведем к виду:

N₀/N = е^-t (1.16.)

Полагая, что N₀/N = 2, а t = T,получимln2 = Т, откуда

ln2 = 0,693 = 0,693/T (1.17.)

Подставив выражение (1.17.) в (1.10.) получим

N = N₀е^-0.693t/T (1.18.)

N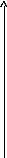

N₀ 1

0,5

0,25

t

0,125

.

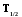
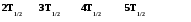
Рис. 1.2. Изменение числа распавшихся ядер исходного элемента со временем.

На графике (рис.1.2.) показана зависимость числа распадающихся атомов от времени. Из графика следует, что в несколько первых полупериодов распад происходит быстро, а затем медленно. Теоретически кривая экспонента никогда не может слиться с осью абсцисс, но на практике можно считать, что примерно через 10 – 20 периодов полураспада радиоактивное вещество распадается полностью.

Основной характеристикой источника радиационного излучения является его активность.

АКТИВНОСТЬ - это физическая величина, характеризующая число радиоактивных распадов в единицу времени.

или

АКТИВНОСТЬ - это отношение числа спонтанных (вероятных) ядерных переходов из определенного ядерно-энергетического состояния радионуклида за интервал времени.

А = . (1.19)

Исходя из определения активности, следует, что активность характеризует скорость ядерных переходов в единицу времени. С другой стороны, количество ядерных переходов зависит от постоянной радиоактивного распада.

Единицей измерения активности в системе СИ является БЕККЕРЕЛЬ (Бк).

Беккерель равен активности источника (радионуклида), в котором за время 1 секунды происходит один спонтанный (вероятностный) переход из определенного ядерно-энергетического состояния этого радионуклида.

Внесистемной единицей измерения активности является КЮРИ (Кu).

Кюри равен активности одного грамма радия.

1 Ku = 3,7 * 10¹⁰ Бк

Отношение активности радионуклидов к единице измерения называется:

к массе - удельной активностью - А_m;

к объему - объёмной активностью - A_v;

к площади - поверхностной активностью - A_s.

Так как АКТИВНОСТЬ характеризует лишь число ядерных переходов, поэтому такие термины, как альфа-, бета-, гамма-активность недопустимы. Так как ядерные превращения не всегда совпадают с числом испускаемых корпускулярных частиц и еще реже - с числом испускаемых фотонов.

Используя уравнение активности (1.19) и уравнение постоянной радиоактивного распада можно получить зависимость изменения активности во времени, а именно:

А =- ,  = - (1.20).

(знак " - " показывает убыль числа ядер - dN). Подставляя в уравнение активности значение dN/dt из уравнения постоянной радиоактивного распада получим А =   N , а так как N в зависимости от времени определяется зависимостью N_t = N₀  e^-t,

выражение активности от времени запишется как

А =N_о е ^-t = N_o exp (-t) = А_o  exp(- t), (1.21)

Однако в процессе радиоактивного распада нас часто интересует не количество ядерных переходов, а масса распавшегося исходного вещества.

Как известно из химии и физики число атомов и масса элемента связаны соотношением:

mN_A

N =  , (1.22)

А

где m-масса элемента (нуклида), N_А - число Авогадро (N_А=6,02210²³ моль^-1), А - атомный вес элемента (массовое число).

Используя зависимость числа атомов через постоянную радиационного распада и выше приведенное соотношение, и их связь с активностью можно определить массу распавшегося радионуклида в процессе радиационного распада за время Т_1/2.

AТ_1/2

m =  , (1.23)

0,693N_А

а так как активность имеет экспоненциальную зависимость, то, преобразуя полученную зависимость массы распавшегося радионуклида во времени, получим выражение

m(t) = m_о  ехр(- t) , (1.24)

Используют также кратную единицу мегакюри 1 Мки = 110⁶ Ки и дольные – милликюри, 1 мКи = 10^-3Ки; микрокюри, 1 мкКи = 10^-6Ки.

А_mможет быть выражена в Бк/кг или Кu/кг;A_sможет быть выражена в Бк/м²или

Кu/ км²;A_vможет быть выражена в Бк/ м³или Кu/ м³.

На практике могут быть использованы как укрупненные, так и дробные единицы измерения. Например: Кu/ км², Бк/см², Бк/г и др.

В нормах радиационной безопасности НРБ-2000 дополнительно введены еще несколько единиц активности, которыми удобно пользоваться при решении задач радиационной безопасности.

Активность минимально значимая (МЗА) - активность открытого источника ионизирующего излучения в помещении или на рабочем месте, при превышении которой требуется разрешение органов санитарно-эпидемиологической службы Министерства здравоохранения на использование этих источников, если при этом также превышено значение минимально значимой удельной активности.

Активность минимально значимая удельная (МЗУА) - удельная активность открытого источника ионизирующего излучения в помещении или на рабочем месте, при превышении которой требуется разрешение органов санитарно-эпидемиологической службы Министерства здравоохранения на использование этого источника, если при этом также превышено значение минимально значимой активности.

Активность эквивалентная равновесная (ЭРОА) дочерних продуктов изотопов радона ²²²Rn и ²²⁰Rn - взвешенная сумма объемных активностей короткоживущих дочерних продуктов изотопов радона - ²¹⁸Ро (RaA); ²¹⁴Pb (RaB); ²¹²Pb (ThB); ²¹²Вi (ThC) соответственно:

(ЭРОА)_Rn = 0,10 А_RaA + 0,52 А_RaB + 0,38 А_RaC ;

(ЭРОА)_Th = 0,91 А_ThB + 0,09 А_ThC ,