
- •Введение
- •1 Основные понятия и определения. Классификация механизмов
- •1.1 Основные понятия и определения
- •1.2 Кинематические пары и их классификация
- •1.3 Кинематические цепи и их классификация
- •1.4 Структурные, кинематические и конструктивные схемы механизмов
- •1.5 Общая классификация механизмов
- •1.5.1 Механизмы, преобразующие вид движения
- •1.5.2 Механизмы, преобразующие параметры движения
- •2 Анализ рычажных механизмов
- •2.1 Структурный анализ
- •2.2 Кинематический анализ
- •2.2.1 Основные кинематические характеристики механизмов
- •2.2.2 Цели, задачи и методы кинематического анализа
- •2.2.3 Графический метод дифференцирования (метод кинематических графиков)
- •2.2.4 Метод планов скоростей и ускорений
- •2.2.5 Понятия об аналитических методах
- •2.3 Силовой анализ
- •2.3.1 Задачи и методы силового анализа
- •2.3.2 Определение внешних сил
- •2.3.3 Трение в кинематических парах
- •2.3.4 Механический КПД машины
- •2.3.5 Определение сил реакций в кинематических парах
- •2.3.6 Кинетостатика ведущего звена (рисунок 2.54)
- •2.3.7 Определение уравновешивающей силы методом Жуковского
- •3 Анализ зубчатых механизмов
- •3.1 Основной закон зацепления (теорема Виллиса)
- •3.2 Теория эвольвенты
- •3.4 Основные параметры эвольвентных зубчатых колес
- •3.5 Способы изготовления зубчатых колес
- •3.6 Основные параметры зубчатой пары
- •3.7 Построение картины внешнего эвольвентного зацепления
- •3.8 Качественные показатели зацепления
- •3.9 Блокирующий контур
- •3.10 Кинематический анализ механизмов передач
- •3.10.1 Аналитический метод
- •3.10.2 Графоаналитический метод
- •3.11 Силовой анализ передач
- •4 Анализ кулачковых механизмов
- •4.1 Общие сведения
- •4.2 Силовой анализ
- •5 Синтез рычажных механизмов
- •5.1 Структурный синтез
- •6 Синтез планетарных механизмов
- •7 Синтез кулачковых механизмов
- •7.1 Графический метод
- •7.1.1 Законы движения ведомого звена
- •7.1.3 Определение основных размеров кулачкового механизма
- •7.1.4 Построение профиля кулачка
- •7.2 Аналитический метод
- •7.2.1 Аналитическое описание закона движения толкателя
- •7.2.2 Определение основных размеров кулачка
- •7.2.3 Построение центрового профиля кулачка
- •7.2.4 Определение радиуса ролика
- •7.2.5 Построение конструктивного профиля кулачка
- •8. Динамика машин с жесткими звеньями
- •8.1 Определение масс и моментов инерции звеньев
- •8.2 Приведение масс
- •8.3 Приведение сил
- •8.4 Режим работы машины
- •8.5 Уравнение движения
- •8.6 Неравномерность хода машинного агрегата
- •8.7 Расчет маховика без учета характеристик приводного электродвигателя
- •8.8 Динамика машин с учетом характеристик приводного электродвигателя
- •9 Динамика машин с учетом упругости звеньев
- •9.1 Структура динамического расчета
- •9.2 Динамические модели
- •9.3 Математические модели
- •9.4 Решение уравнений движения
- •9.5 Оптимизация колебательного процесса
- •10 Уравновешивание и виброзащита машин
- •10.1 Уравновешивание машин
- •10.1.1 Уравновешивание вращающихся звеньев
- •10.1.2 Уравновешивание плоских рычажных механизмов (циклических механизмов)
- •10.2 Виброзащита машин
- •10.2.1 Виброгашение
- •10.2.2 Виброизоляция
- •11 Манипуляторы и промышленные роботы
- •11.1 Виды манипуляторов и промышленных роботов
- •11.2 Структура и геометрия манипуляторов
- •11.3 Кинематика манипуляторов
- •12 Синтез системы управления механизмами машины-автомата
- •12.1 Тактограмма движения
- •12.2 Таблица включений (таблица 12.2)
- •12.3 Составление формул включения и их упрощение
- •12.4 Построение системы управления на пневматических элементах
- •12.5 Построение системы управления на электрических элементах
- •Список использованных источников
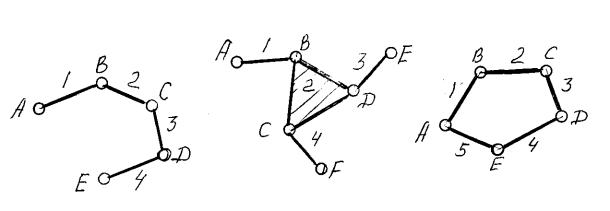
1.3 Кинематические цепи и их классификация
Кинематическая цепь – это связанная система звеньев, образующих между собой кинематические пары.
Кинематические цепи делятся на:
а) простые, если каждое звено входит не более, чем в две кинематические пары (рисунок 1.6а, в) и сложные, если хотя бы одно звено входит более, чем в две кинематические пары (рисунок 1.6б);
а) |
б) |
в) |
Рисунок 1.6
б) открытые (незамкнутые), если есть звенья, входящие только в одну кинематическую пару (рисунок 1.6а, б) и закрытые (замкнутые), если каждое звено входит по крайней мере в две кинематические пары (рисунок 1.6в);
в) плоские и пространственные (аналогично кинематическим парам). Число степеней свободы кинематической цепи относительно одного из ее звеньев называют степенью подвижности – W. Степень подвижности является структурной характеристикой кинематической цепи и механизма в целом.
Если число подвижных звеньев – n, то общее число степеней свободы до соединений их в кинематическую цепь равно Н = 6n.
Соединяясь между собой и со стойкой в кинематические пары различной степени подвижности у кинематической цепи отнимаются степени свободы в зависимости от класса кинематической пары.
Тогда степень подвижности кинематической цепи
W = H − S å = 6n − ( 5P1 + 4P2 + 3P3 + 2P4 + P5 ) , |
(1.1) |
или структурная формула общего вида для пространственных механизмов, где P1 ,P2 ,P3 ,P4 ,P5 - число кинематических пар одно, двух, трех, четырех и пяти подвижности. В плоских механизмах из шести возможных
движений три не |
могут быть осуществлены: одно поступательное, |
перпендикулярное |
плоскости |
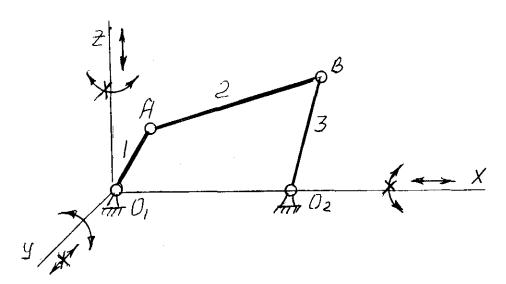
механизма (XOZ) и два вращательных вокруг осей X, Z определяющих эту плоскость (рисунок 1.7).
Рисунок 1.7
Тогда, степень подвижности плоского механизма
W = (6 − 3)n − (5 − 3)P1 − (4 − 3)P2 − (3 − 3)P3 ,
или
(1.2)
W = 3n − 2P1 − P2 - (формула Чебышева 1869 г.)*
В состав плоского механизма кинематические пары Р5, Р4, Р3 входить не могут, как обладающие пространственным характером возможных относительных движений.
Степень подвижности плоских рычажных механизмов с одноподвижными кинематическими парами (у которых Р2 = 0)
W = 3n − 2P1. |
(1.3) |
Для кривошипно-коромыслового механизма (рисунок 1.7) |
|
n = 3, P1 = 4, |
|
W = 3 × 3 - 2 × 4 = 1 |
|
Степень подвижности показывает количество ведущих звеньев в механизме.
____________________________________________________________________
* Чебышев Пафнутий Львович (1821-1894) – знаменитый русский математик и механик. Написал 15 работ по теории механизмов.
1.4 Структурные, кинематические и конструктивные схемы механизмов
Для уяснения общего принципа работы, любой механизм может быть представлен структурной схемой, т.е. может быть изображен графически, без учета масштаба с применением условных обозначений звеньев и кинематических пар. Например, на рисунке 1.4 представлена структурная схема кривошипно-коромыслового механизма.
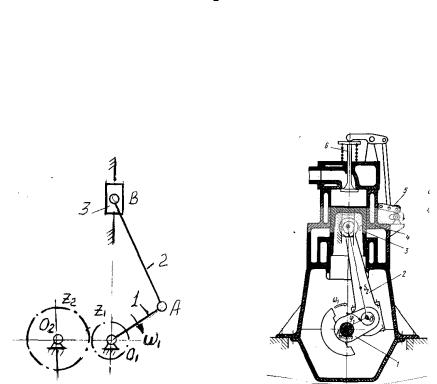
Чтобы изучить движение механизма (кинематические характеристики) необходимо знать размеры всех звеньев, направление и частоту вращения ведущего звена и т.д. Для этого составляют кинематическую схему механизма, которая строится в выбранном масштабе, с точным соблюдением всех размеров и форм звеньев, с указанием направления движения ведущего звена. На рисунке 1.8 представлена кинематическая схема кривошипноползунного механизма, где звено 3 – ползун, совершает возвратнопоступательное движение относительно неподвижной направляющей.
Масштабный коэффициент μl = l/l м/мм означает, что 1 мм чертежа соответствует μl метрам натуральной длины звеньев.
Кинематическая схема должна иметь все параметры необходимые для кинематического анализа: длины звеньев, числа зубьев зубчатых колес, профили элементов высших кинематических пар (кулачков) и т.д.
Рисунок 1.8 |
Рисунок 1.9 |
Конструктивные особенности звеньев, не оказывающих влияние на движение механизма, на кинематической схеме не изображаются. Если эти особенности нужно учесть, то составляют конструктивную схему механизма, (рисунок 1.9).
