
- •Введение
- •1 Основные понятия и определения. Классификация механизмов
- •1.1 Основные понятия и определения
- •1.2 Кинематические пары и их классификация
- •1.3 Кинематические цепи и их классификация
- •1.4 Структурные, кинематические и конструктивные схемы механизмов
- •1.5 Общая классификация механизмов
- •1.5.1 Механизмы, преобразующие вид движения
- •1.5.2 Механизмы, преобразующие параметры движения
- •2 Анализ рычажных механизмов
- •2.1 Структурный анализ
- •2.2 Кинематический анализ
- •2.2.1 Основные кинематические характеристики механизмов
- •2.2.2 Цели, задачи и методы кинематического анализа
- •2.2.3 Графический метод дифференцирования (метод кинематических графиков)
- •2.2.4 Метод планов скоростей и ускорений
- •2.2.5 Понятия об аналитических методах
- •2.3 Силовой анализ
- •2.3.1 Задачи и методы силового анализа
- •2.3.2 Определение внешних сил
- •2.3.3 Трение в кинематических парах
- •2.3.4 Механический КПД машины
- •2.3.5 Определение сил реакций в кинематических парах
- •2.3.6 Кинетостатика ведущего звена (рисунок 2.54)
- •2.3.7 Определение уравновешивающей силы методом Жуковского
- •3 Анализ зубчатых механизмов
- •3.1 Основной закон зацепления (теорема Виллиса)
- •3.2 Теория эвольвенты
- •3.4 Основные параметры эвольвентных зубчатых колес
- •3.5 Способы изготовления зубчатых колес
- •3.6 Основные параметры зубчатой пары
- •3.7 Построение картины внешнего эвольвентного зацепления
- •3.8 Качественные показатели зацепления
- •3.9 Блокирующий контур
- •3.10 Кинематический анализ механизмов передач
- •3.10.1 Аналитический метод
- •3.10.2 Графоаналитический метод
- •3.11 Силовой анализ передач
- •4 Анализ кулачковых механизмов
- •4.1 Общие сведения
- •4.2 Силовой анализ
- •5 Синтез рычажных механизмов
- •5.1 Структурный синтез
- •6 Синтез планетарных механизмов
- •7 Синтез кулачковых механизмов
- •7.1 Графический метод
- •7.1.1 Законы движения ведомого звена
- •7.1.3 Определение основных размеров кулачкового механизма
- •7.1.4 Построение профиля кулачка
- •7.2 Аналитический метод
- •7.2.1 Аналитическое описание закона движения толкателя
- •7.2.2 Определение основных размеров кулачка
- •7.2.3 Построение центрового профиля кулачка
- •7.2.4 Определение радиуса ролика
- •7.2.5 Построение конструктивного профиля кулачка
- •8. Динамика машин с жесткими звеньями
- •8.1 Определение масс и моментов инерции звеньев
- •8.2 Приведение масс
- •8.3 Приведение сил
- •8.4 Режим работы машины
- •8.5 Уравнение движения
- •8.6 Неравномерность хода машинного агрегата
- •8.7 Расчет маховика без учета характеристик приводного электродвигателя
- •8.8 Динамика машин с учетом характеристик приводного электродвигателя
- •9 Динамика машин с учетом упругости звеньев
- •9.1 Структура динамического расчета
- •9.2 Динамические модели
- •9.3 Математические модели
- •9.4 Решение уравнений движения
- •9.5 Оптимизация колебательного процесса
- •10 Уравновешивание и виброзащита машин
- •10.1 Уравновешивание машин
- •10.1.1 Уравновешивание вращающихся звеньев
- •10.1.2 Уравновешивание плоских рычажных механизмов (циклических механизмов)
- •10.2 Виброзащита машин
- •10.2.1 Виброгашение
- •10.2.2 Виброизоляция
- •11 Манипуляторы и промышленные роботы
- •11.1 Виды манипуляторов и промышленных роботов
- •11.2 Структура и геометрия манипуляторов
- •11.3 Кинематика манипуляторов
- •12 Синтез системы управления механизмами машины-автомата
- •12.1 Тактограмма движения
- •12.2 Таблица включений (таблица 12.2)
- •12.3 Составление формул включения и их упрощение
- •12.4 Построение системы управления на пневматических элементах
- •12.5 Построение системы управления на электрических элементах
- •Список использованных источников
В качестве самоконтроля при построении диаграммы перемещения необходимо учесть, что ордината, соответствующая концу фазы подъема, должна давать (приближенно) значение ходя толкателя или коромысла, ордината, получающаяся в конце фазы опускания, должна (приближенно) равняться нулю.
7.1.3 Определение основных размеров кулачкового механизма
Кулачковый механизм с роликовым толкателем (рисунок 7.4).
Эксцентриситет е, угол α доп и направление вращения кулачка заданы
(вращение против часовой стрелки).
Все три диаграммы движения толкателя построены и все масштабные коэффициенты определены (рисунок 7.3).
Необходимо определить минимальное расстояние от центра вращения кулачка до начального положения центра ролика - ro = O1A0 , при котором переменный угол давления ни в одном положении кулачкового механизма не будет больше α доп .
Из рисунка 7.4 имеем, минимальный радиус центрового профиля
ro = r + rрол ,
где r – радиус окружности, вписанной в конструктивный профиль; rрол – радиус ролика толкателя.
Построим диаграмму перемещения толкателя в функции от аналога скорости S = S(S' ) (рисунок 7.5). Начало координат диаграммы совпадает с
начальным положением центра ролика (точка Ао) ось ординат направлена в сторону подъема толкателя и на ней откладываем ординаты с диаграммы перемещения S = S(ϕ ) .
Направление оси абсцисс получено поворотом оси ординат на 900 в направлении вращения кулачка на фазе подъема и в противоположную сторону на фазе опускания и вдоль ее откладываем значения с диаграммы
аналога скорости S' = S' (ϕ ) .
Масштабные коэффициенты должны быть равны между собой и равны масштабному коэффициенту построения μS' = μS = μl .
Получаем точки а1, а2, а3 ... а12 на фазе подъема и точки а13, а14 ... а25 – на фазе опускания. Соединяя эти точки плавной линией получаем диаграмму
S= S(S' ) .
Кпостроенной диаграмме проведем касательную τ под углом α доп к
оси S на фазе подъема и касательную τ под углом α доп на фазе опускания (обычно α доп > α доп , в курсовых проектах α доп = α доп ).
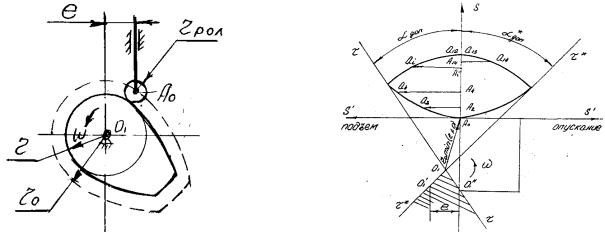
Острый угол τ о1τ (заштрихован) определяет на плоскости геометрическое место точек, каждую из которых можно принять за центр вращения кулачка, где α < α доп . tgα i = S' /(r + Si ).
Точке О1 – соответствует наименьшее значение начального радиуса -
ro min .
Если смещение е задано, то наименьшему значению будет соответствовать точка O'1 (если е = 0, то O"1 ).
Следует отметить, что чем ниже располагать центр вращения кулачка внутри угла, тем меньше будет угол передачи движения, тем лучше будут условия
Рисунок 7.4 |
Рисунок 7.5 |
работы механизма. Однако, одновременно с этим будет увеличиваться начальный радиус ro и, следовательно, размеры кулачка.
Радиус ролика выбирается из условий:
- радиус ролика rрол должен быть меньше ρ min - наименьшего радиуса
кривизны центрового профиля на выпуклых участках, т.к. в противном случае конструктивный профиль будет иметь самопересечение, обычно
принимают rрол ≤ 0,8ρ min ;
- вторым ограничением является неравенство rрол ≤ 0,4ρ 0 рекомендуемое из конструктивных соображений.
Кулачковый механизм с роликовым коромыслом (рисунок 4.1г).
Предполагаем, что все три диаграммы движения построены и все масштабные коэффициенты определены. Длина коромысла l2, угол α доп ,
величина и направление вращения кулачка заданы (вращение против часовой стрелки).
Необходимо определить минимальные значения центрового профиля радиуса romin и расстояния между центрами вращения кулачка и коромысла lо при которых переменный угол давления α в любом положении кулачкового механизма будет меньше α доп (причем γ = 900 − α ).
Учитывая равенство масштабных коэффициентов μ S" = μ S' = μ S = μ l ,
строим начальное положение коромысла О2А0 (центр вращения и направление коромысла выбираем произвольно) и через точку Ао проводим траекторию центра ролика (рисунок 7.6). На траектории откладываем отрезки

А0 А1 , А0 А2 , А0 Аi с диаграммы перемещений S. (Длину дуги
окружности, если она не больше 100, можно считать равной длине хорды). Если дуга превышает 100, то ее надо разделить на части. После
разметки траектории точки А, проводим прямые 02 А1 , 02 А2 , ..., 02 Аi ,
ина них откладываем отрезки Аiai , длины которых равны
соответствующим ординатам на диаграмме аналога скорости S’. Направление этого отрезка на фазе подъема откладываем от центра
вращения О2, если кулачок и коромысло вращается в противоположных направлениях, и к центру О2, если они вращаются в одну сторону (т.е. поворот вектора скорости точки Аi на 900 в направлении вращения кулачка), Указанные построения дают геометрическое место точек а1, а2, ..., а12 на фазе подъема, и точки а13, а14, ..., а25 на фазе опускания. Соединяя точки аi плавной линией, получаем диаграмму S = S(S’).
Из точек аi под углом (900 - α доп ) к отрезку Аiai на фазе подъема и под углом (900 - α *доп ) на фазе опускания проводим лучи τ i и τ *i . В курсовых
проектах лучи τ i и τ *i достаточно провести из трех крайних точек аi с
каждой стороны диаграммы S = S(S’).
В следствии приближенности всех расчетов, связанных с допускаемым углом давления, допускаемая зона для центра вращения кулачка практически
располагается между прямыми τ и τ * , имеющими наименьшую точку
пересечения – О1 (заштрихованная область).
Выбранное в допускаемой зоне положение центра кулачка О1 определяет искомый начальный радиус - romin и расстояние между центрами вращения кулачка и коромысла О1О2 = lо.
Кулачковый механизм с плоским толкателем (рисунок 4.1в).
Основными размерами в кулачковом механизме с плоским толкателем являются – r – начальный радиус профиля кулачка (радиус окружности, вписанной в конструктивный профиль кулачка) и размер тарелки толкателя – rт. Причем, расстояние от оси толкателя (проходящей через центр вращения кулачка) до точки контакта его с профилем кулачка равно аналогу скорости
S’.
При вращении кулачка против часовой стрелки эта точка расположена при подъеме справа, а при опускании – слева от оси толкателя (при вращении кулачка по часовой стрелке – наоборот). Из сказанного следует, что величина тарелки толкателя должна превышать наибольшее значение модуля аналога скорости толкателя и при подъеме вп и при опускании во, т.е. должно быть
выполнено условие rт > вп ,во .
Величину начального радиуса кулачка можно получить графически, строя диаграмму перемещения в функции от аналога ускорения S = S(S”) (рисунок 7.7). По оси абсцисс откладываем значения аналога ускорений S” по
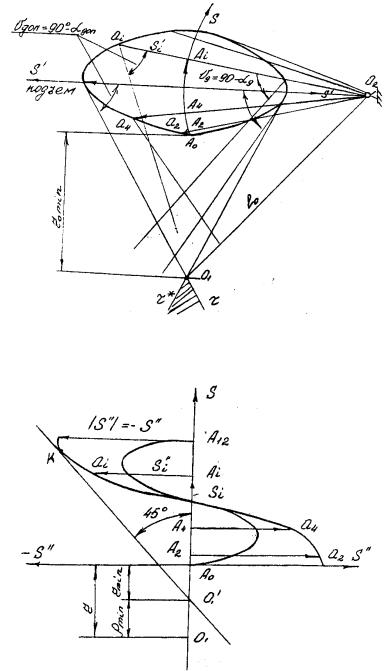
оси ординат величину перемещений S, которые берем соответственно с диаграммы аналога ускорения и диаграммы перемещения. После этого
Рисунок 7.6
Рисунок 7.7
проводим под углом 450 к оси абсцисс прямую так, чтобы она касалась снизу одной из ветвей диаграммы с отрицательными абсциссами. Отрезок 0′1 А0 ,
который отсекает эта прямая на отрицательном направлении оси ординат определяет искомую величину rmin, т.е. такое значение r, при котором радиус
кривизны профиля хотя бы в одной точке (такая точка на профиле соответствует К – точке касания прямой с диаграммой) обращается в ноль, но отрицательных значений иметь не может.
