
Engineering and Manufacturing for Biotechnology - Marcel Hofman & Philippe Thonart
.pdfPART II
PROCESS MODELLING
MATHEMATICAL MODELLING OF MICROBIAL PROCESSES – MOTIVATION AND MEANS
TEIT AGGER AND JENS NIELSEN
Center for Process Biotechnology, Department of Biotechnology, Technical University of Denmark, Building 223, DK-2800 Lyngby,
Denmark.
Abstract
In this paper the motivation for using mathematical models to describe microbial processes is discussed. Mathematical models have a unique ability to extract information from the wealth of experimental data constantly accumulating in the fields of basic and applied microbiology. They allow for detailed investigations of the interactions in complex biological systems that are otherwise practically impossible.
Modelling can be applied to optimise the performance of industrial processes, e.g. by use in advanced control algorithms or by simulating different operating conditions.
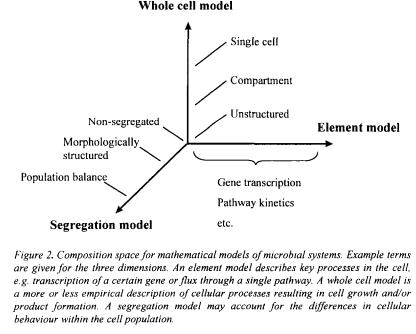
Furthermore, mathematical models used for computer simulations of microbial processes are invaluable educational tools. Mathematical models can be grouped in three classes - whole cell models, segregation models and element models. A whole cell model describes growth and product formation, often in an empirical fashion. A segregation model is used to describe different cell types, and element models are used to give detailed mechanistic descriptions of specific processes. Any level of detail can be included in each of the three classes of models, and the different models may be combined when a fermentation process is to be described. Here a general mathematical framework is given for whole cell models and a few examples of relatively simple, yet very applicable, models are given.
1. Introduction
Modern biotechnology is a rapidly growing discipline encompassing an enormous range of applications. Common to all applications, however, is the involvement of life processes at some stage, directly or indirectly. One such process is the growth of microorganisms, a process used extensively in many of modern society’s vital industries, such as the manufacturing of food, alcoholic beverages, pharmaceuticals, fine chemicals and enzymes. Although micro-organisms are relatively simple life forms their growth is the result of a machinery of immense complexity, involving sophisticated molecular
61
M. Hofman and P. Thonart (eds.), Engineering and Manufacturing for Biotechnology, 61–75. © 2001 Kluwer Academic Publishers. Printed in the Netherlands.
Teit Agger and Jens Nielsen
processes in which numerous genes, proteins and metabolites take part. This intrinsic complexity of microbial growth, coupled with the fact that far from all aspects of the growth processes are known at present, makes the analysis, development and optimisation of processes that involve the growth of micro-organisms a difficult task. One way of approaching this task in a rational manner is by using mathematical models. These models can help in structuring the wealth of information constantly accumulating in the field, extracting correlations that would otherwise be difficult, if not impossible, to discover. They can increase our understanding of the multitude of processes occurring in the microbial cells and their complex interplay, thereby enabling more rational and efficient experimental strategies to be developed. This paper presents an overview of the purposes and applications of mathematical modelling of microbial growth as well as some of the tools needed, i.e. general mathematical frameworks.
2. Motivation
Mathematical modelling is a powerful scientific tool, but when applying mathematical models to microbial processes it is very important to clearly state the reasoning for setting up the model and using it for simulations. The model should aim at fulfilling a
purpose other than just fitting experimental |
data, which is rarely of any scientific value. |
In the following a few of the many good |
reasons for using mathematical models are |
discussed.
Experimental research involving microbial processes often produces large amounts of data and it can be difficult if not impossible to interpret these data without the aid of mathematical models. The ability of mathematical models to extract information is invaluable in the processing and comparison of experimental data. An example of this is the use of simple mathematical models to quantify the morphology of filamentous fungi
- Spohr et al. (1997) measured the average total hyphal length and the average number of tips of three different strains of Aspergillus oryzae during submerged growth. Using simple mathematical models, parameters such as the maximal tip extension rate and the maximal branching frequency were extracted from the data, enabling the investigators to easily compare the different strains examined. The concepts of metabolic flux analysis and metabolic control analysis can also be used to extract valuable information from experimental data concerning the magnitude of intracellular fluxes and the degree to which different enzymatic steps in the metabolism are rate controlling. Using 13C- labelled substrates metabolic pathways can be analysed in even greater detail, and information on new pathways or the intracellular localisation of reactions can be obtained. This information can then be used to target an experimental effort in order to increase productivity for example. An example of this is the work of Pedersen et al. (1999) who, using metabolic flux analysis, found an increase of 15-26 % in the flux through the pentose phosphate pathway in a recombinant A. oryzae producing higher levels of  amylase than the wild type. Work on recombinant Bacillus subtilis producing riboflavin (Sauer et al., 1997) also showed that the pentose phosphate pathway is a major pathway for carbon catabolism.
amylase than the wild type. Work on recombinant Bacillus subtilis producing riboflavin (Sauer et al., 1997) also showed that the pentose phosphate pathway is a major pathway for carbon catabolism.
62
Mathematical Modelling of Microbial Processes
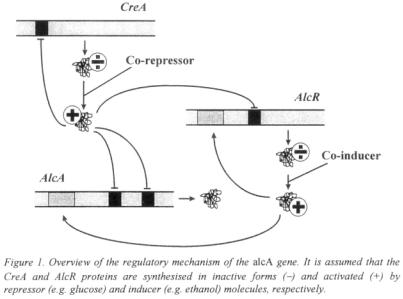
The complex nature of biological systems often makes it a very hard task to predict the effects of an alteration of the system just by looking at it. The use of mathematical models to examine the interactions in a complex system by describing individual parts and their interplay makes such predictions possible. As an example, control of gene expression is a highly complex process, often involving several regulatory proteins, and predicting the effects of performing changes in the genes involved is not an easy task. Lee and Bailey (1984a-c) used a mechanistic approach to model the lac operon in E. coli and were able to correctly predict the effects of mutations in the genes involved. They also investigated how the efficiency of a cloned lac promoter depends on the number of promoters per cloning vector and the cloning vector size. A similar approach was used by Agger and Nielsen (1999) for modelling the alcA system in A. nidulans, a system with a fairly complex regulatory structure involving a represser (CreA), an inducer (AlcR) and the structural gene (alcA) interacting as shown in Figure 1 (Mathieu and Felenbok, 1994).
The general features of this regulatory system are similar to many other systems, e.g. regulation of  amylase production in Aspergillus oryzae and regulation of the gal- genes in Saccharomyces cerevisiae. Estimation of model parameters such as binding affinities of regulatory proteins to target genes were based on experimental data on intracellular levels of mRNA and protein obtained by Panozzo et al. (1998). By changing only the relevant parameters the model was able to simulate the effects of genetic alterations such as deletion of represser sites in the structural gene and expression of an extra copy of the activator gene with a constitutive promoter.
amylase production in Aspergillus oryzae and regulation of the gal- genes in Saccharomyces cerevisiae. Estimation of model parameters such as binding affinities of regulatory proteins to target genes were based on experimental data on intracellular levels of mRNA and protein obtained by Panozzo et al. (1998). By changing only the relevant parameters the model was able to simulate the effects of genetic alterations such as deletion of represser sites in the structural gene and expression of an extra copy of the activator gene with a constitutive promoter.
Models like these contain systems of non linear differential equations with many parameters, the numerical solution of which pose a heavy computational burden.
63
Teit Agger and Jens Nielsen
However, with the explosive development in computing power this is not a practical problem and simulations using even very complex models can be routinely performed on desk-top computers. These highly mechanistic and extremely detailed models hold the potential for enabling investigators to test hypotheses concerning the interactions in regulatory systems without spending hours in the laboratory. They are able to aid in experimental planning by pointing towards the targets of manipulation that will most likely have the desired impact on the system. And as genomic sequence data continues to build up with ever increasing speed, they will be invaluable in interpreting this wealth of information. In theory, models like these will eventually form the basis for a complete, mechanistic description of all events in the cell.
Another, more practical, use of mathematical models is for optimising the performance of industrialfermentation processes. When producing Bakers yeast by fedbatch fermentation with S. cerevisiae, control of the feed rate is important. If it is too high, the yeast will produce ethanol, thereby significantly reducing the yield of biomass on substrate. On the other hand, the productivity of the process increases with the feed rate that makes it desirable to operate at a feed rate just below that resulting in ethanol formation. Since a fed-batch fermentation is a dynamic process with a constantly changing biomass concentration the feed rate has to be adjusted throughout the fermentation. A way of optimising the process performance is by applying a control strategy involving information about the metabolism of the micro-organism in the form of a mathematical model (internal model control) which allows for a faster and more precise regulation. Model based regulation can also be used for effective control of the dissolved oxygen tension and the feed rate during production of products such as penicillin. If the process model is sufficiently robust it can be used for designing and optimising fermentation processes as well, e.g. choosing the optimal feeding strategy for a fed-batch fermentation.
Mathematical models are also excellent educational tools for teaching everything from basic fermentation technology to advanced metabolic pathway analysis. Interactive illustrations of microbial processes based on mathematical models are fast, comprehensive and inexpensive and are valuable supplements to laboratory training of students. Simulations allow students to explore the dynamics of microbial systems, obtaining instant results and covering many subjects in a short time.
3. Means - General modelling frameworks
A biochemical system involving microbial cells is by nature very complex and heterogeneous. It includes a huge array of chemical compounds ranging from simple metabolites to extremely complex macromolecules, it involves interactions on many levels and exhibits dynamics spanning a wide timescale. This makes a complete mathematical description of such a system virtually impossible and any modelling effort will therefore result in a more or less crude approximation. Keeping this in mind, it is obvious that the modelling should strive to capture the most important elements of the system, these being determined by the purpose of the modelling exercise. As an example, if one wants to be able to quantify the impact of genetic changes on the
64
Mathematical Modelling of Microbial Processes
morphology of a micro-organism it is most likely of little use to focus on a detailed description of primary carbon catabolism. It is thus essential to clearly define the intended use of the model before initiating the mathematical description of the system.
When modelling a microbial process one has to take into account the environment in which the organisms are growing, i.e. the bioreactor. If the dynamics of the processes that the model is supposed to describe are much slower than those of the bioreactor, then the environment can be assumed to be homogenous (‘ideal’ bioreactor). However, even in small-scale laboratory bioreactors the time of e.g. substrate mixing can be sufficiently long to have a major impact on cellular processes, and then the mass transfer and flow patterns in the bioreactor have to be given special attention. This treatment is out of the scope of this text and hence the models considered here will refer to a homogenous environment.
When constructing a mathematical model for a microbial system, three basic questions have to be posed:
•How detailed does the general functions (e.g. substrate uptake, product formation)
|
of the cell have to be described? |
• |
Does the application of the model require any element of the cellular functions to |
|
be modelled in detail? |
•Are the cells to be treated as average cells or is a description of several different cell types required?
65
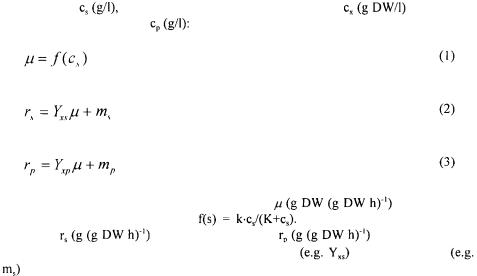
Teit Agger and Jens Nielsen
The answers to these three questions will place the model composition somewhere in the space outlined in Figure 2. The element model will often be a highly detailed, mechanistic model of certain cellular functions, whereas the whole cell model gives an empirical description of e.g. substrate uptake and product formation. In theory, a whole cell model can be constructed from a large net of detailed element models describing all the key processes involved in cell growth, e.g. gene transcription, protein synthesis, catabolism and anabolism. However, this is practically impossible and only the elements of cellular function relevant to the specific application are normally included in the element model, the remaining functions being described in a more or less empirical fashion by a whole cell model.
Traditionally, a mathematical model of a microbial system is referred to as being ‘unstructured’ if only one variable (e.g. biomass concentration) is used to describe the cells, whereas ‘structured’ models make use of several variables (Fredrickson et al., 1970). Similarly, a ‘non-segregated’ model describes all cells in the system considered as being equal whereas a ‘segregated’ model includes a description of the variation between cells (Ramkrishna, 1979). The simplest model is thus the unstructured, nonsegregated model given in Eq. (1) - (3) for growth on a single substrate with
concentration |
formation of biomass with concentration |
and a single |
product with |
concentration |
|
Biomass is formed with |
a specific growth rate of |
which is |
often |
||
described by Monod kinetics, i.e. |
|
The specific rates of substrate |
|||
utilisation |
and |
product |
formation |
are given as |
linear |
functions of the specific growth |
rate µ |
with the yield |
and maintenance |
|
|
coefficients being constants. |
Although completely empirical, this very simple model |
||||
performs rather well in a number of situations, especially when substrate is plentiful and balanced growth prevails (all internal cell components grow at the same rate). However, the model does not supply any information about the processes occurring during growth of the micro-organism and it will most likely fail when the growth situation becomes just a little more complex.
If a model is needed that is able to describe microbial growth during a broader range of conditions, the model structure has to incorporate more detailed descriptions of the processes taking place. These descriptions can be included by extending the model complexity along one or more of the three axes shown in Figure 2, e.g. in an empirical fashion by including more detail in the whole cell model or by a description of different
66

Mathematical Modelling of Microbial Processes
cell types or morphology and also in a mechanistic fashion by including an element model employing descriptions based on the vast amount of knowledge available on the biochemistry and genetics of microorganisms. Depending on the purpose of the model, one or more of these subjects can be predominant in the model structure, thus giving rise to e.g. ‘morphologically structured’ models or ‘genetically structured’ models. A general framework for the biochemistry of microbial cells, based on that of Nielsen and
Villadsen (1992), is given below. It incorporates Q morphological forms each having J intracellular reactions involving L intracellular components (X), N substrates (s) and M metabolic products (p). All biochemical reactions, including substrate uptake and product excretion, can be described by eq. (4) whereas eq. (5) describes K irreversible
metamorphosis reactions, converting one morphological form (with mass fraction Zq) to another:
A mass balance for the intracellular components yields eq. (6) in which R is the net rate of formation of the cell component vector
The |
matrix contains the stoichiometric |
coefficients, |
is the rate vector of the |
reactions (4) for the 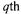 morphological form,
morphological form,  are matrices containing the negative and positive stoichiometric
are matrices containing the negative and positive stoichiometric  coefficients, respectively,
coefficients, respectively, 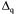 is the qth column of
is the qth column of
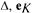 is a vector with K elements, all being unity, u is a diagonal
is a vector with K elements, all being unity, u is a diagonal 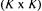 matrix which contains the rates of the metamorphosis reactions and
matrix which contains the rates of the metamorphosis reactions and 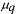 is the specific growth rate of the qth morphological form. The first term on the right hand side of eq. (6) thus describes the change in the cell component vector X, caused by the reactions given in eq. (4), the second term gives the change caused by the metamorphosis reactions and the third term describes the dilution caused by growth. Mass balances for a bioreactor with sterile feed are given in eqs. (7) - (11):
is the specific growth rate of the qth morphological form. The first term on the right hand side of eq. (6) thus describes the change in the cell component vector X, caused by the reactions given in eq. (4), the second term gives the change caused by the metamorphosis reactions and the third term describes the dilution caused by growth. Mass balances for a bioreactor with sterile feed are given in eqs. (7) - (11):
67

Teit Agger and Jens Nielsen
Here M is a 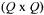 diagonal matrix with
diagonal matrix with 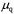 in the diagonal,
in the diagonal,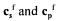 are the inlet concentrations of substrates and products, respectively, D is the dilution rate and
are the inlet concentrations of substrates and products, respectively, D is the dilution rate and
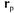 are given by
are given by
with the matrices 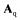 and
and 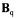 containing the stoichiometric
containing the stoichiometric 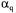 and
and 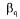 coefficients, respectively. The specific growth rate
coefficients, respectively. The specific growth rate 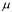 of the total biomass is given by
of the total biomass is given by
where 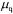 is the specific growth rate of the qth morphological form. With sterile feed, the dilution rate D is zero for a batch cultivation,
is the specific growth rate of the qth morphological form. With sterile feed, the dilution rate D is zero for a batch cultivation, 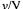 for a continuous cultivation and
for a continuous cultivation and
68

Mathematical Modelling of Microbial Processes
for a fed-batch cultivation. The mass balances (7) - (11) can be used to describe a segregated model to the level of a morphologically structured model containing a finite number Q of cell types and a whole cell model containing any level of detail. If an infinite number of cell types are to be considered the mass balances changes to
where |
is a dimensionless discrete distribution function of cell forms, normalised |
by |
|
with the average property vector 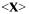 given by:
given by:
The element models will often need a customised mathematical framework to deal with the processes in question. If a description of gene transcription, translation and regulation is needed, a general framework is given in Agger and Nielsen (1999) based on the work of Lee and Bailey (1984a-c). The model is based on a description of the
69
