
- •Типовой расчет «Функции нескольких переменных»
- •Вариант № 1
- •1. Найдите область определения функций:
- •Вариант № 2
- •Вариант № 3
- •1. Найдите область определения функций :
- •Вариант № 4
- •1. Найдите область определения функции :
- •Вариант № 5
- •1. Найдите область определения функций:
- •Вариант № 6
- •1. Найдите область определения функций :
- •Вариант № 7
- •1. Найдите область определения функций:
- •Вариант № 8
- •1. Найдите область определения функций :
- •Вариант № 9
- •1. Найдите область определения функций :
- •Вариант № 10
- •1. Найдите область определения функций :
- •Вариант № 11
- •1. Найдите область определения функций :
- •Вариант № 12
- •1. Найдите область определения функций :
- •Вариант № 13
- •1. Найдите область определения функций :
- •Вариант № 14
- •1. Найдите область определения функций :
- •Вариант № 15
- •1. Найдите область определения функций :
- •Вариант № 16
- •1. Найдите область определения функций :
- •Вариант № 17
- •1. Найдите область определения функций :
- •Вариант № 18
- •1. Найдите область определения функций :
- •Вариант № 19
- •1. Найдите область определения функций :
- •Вариант № 20
- •1. Найдите область определения функций :
- •Вариант № 21
- •1. Найдите область определения функций :
- •Вариант № 22
- •1. Найдите область определения функций :
- •Вариант № 23
- •1. Найдите область определения функций :
- •Вариант № 24
- •1. Найдите область определения функций :
- •Вариант № 25
- •1. Найдите область определения функций :
- •Вариант № 26
- •1. Найдите область определения функций :
- •Вариант № 27
- •1. Найдите область определения функций :
- •Вариант № 28
- •1. Найдите область определения функций :
- •Вариант № 29
- •1. Найдите область определения функций:
- •Вариант № 30
- •1. Найдите область определения функций:

Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения
Э. Е. Поповский П. П. Скачков
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Типовой расчет
Екатеринбург
2010
Федеральное агентство железнодорожного транспорта Уральский государственный университет путей сообщения Кафедра «Высшая математика»
Э. Е. Поповский П. П. Скачков
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Типовой расчет
Учебно-методическое пособие для студентов всех специальностей
Екатеринбург
2010
УДК 517.1 П 58
Поповский, Э. Е.
П 58 Функции нескольких переменных. Типовой расчет : учеб.-метод. пособие для студентов всех специальностей / Э. Е. Поповский, П. П. Скачков. − Екатеринбург : УрГУПС, 2010. − 44 с.
Пособие предназначено для выполнения индивидуальных заданий типового расчета по теме «Функции нескольких переменных» студентами всех специальностей дневной формы обучения.
Первая часть пособия содержит краткие теоретические сведения, необходимые для решения задач типового расчета. Рассмотрены примеры для всех типов заданий. Приведены подробные решения наиболее важных из них с необходимыми пояснениями и ссылками на теоретический материал.
Вторая часть представляет собой индивидуальные задания. По уровню сложности и тематике они носят характер, соответствующий требованиям программы по математике для технических вузов.
УДК 517.1
Пособие рекомендовано к изданию на заседании кафедры«Высшая математика», протокол № 9 от 21.09. 2010 г.
Авторы: Э. Е. Поповский, доцент кафедры «Высшая математика», УрГУПС;
П. П. Скачков, доцент кафедры «Высшая математика», канд. физ.-мат. наук, УрГУПС
Рецензенты: Г. А. Тимофеева, профессор кафедры «Высшая математика», д-р физ.-мат. наук, УрГУПС;
Л. Ф. Спевак, старший научный сотрудник ИМ УрО РАН, канд. физ.-мат. наук
ÓУральский государственный университет путей сообщения (УрГУПС), 2010
|
ОГЛАВЛЕНИЕ |
|
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ................................................................... |
4 |
|
1. |
Область определения функции нескольких переменных…................... 4 |
|
2. |
Линии уровня функции .............................................................................. |
7 |
3. |
Предел и непрерывность функции двух переменных .............................. |
9 |
4. |
Дифференцирование функции двух переменных................................... |
10 |
5. |
Дифференцирование неявных функций двух переменных…………….12 |
|
6. |
Полный дифференциал функции............................................................. |
13 |
7. |
Касательная плоскость и нормаль к поверхности .................................. |
14 |
8. |
Производная по направлению и градиент функции……………………16 |
|
9. |
Частные производные второго порядка .................................................. |
18 |
10. Экстремум функции ............................................................................. |
19 |
|
11. Наибольшее и наименьшее значение функции .................................... |
24 |
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ......................................................... |
26 |
|
Типовой расчет «Функции нескольких переменных» ........................................ |
27 |
|
3
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1. Область определения функции нескольких переменных
Ранее было введено понятие функции одной переменной. Однако многие задачи физики, техники, экономики и . тд. приводят к рассмотрению переменной величины, которая связана зависимостью с двумя или более независимо изменяющимися переменными. Отсюда вытекает необходимость
оперировать |
|
|
с |
так |
называемыми |
функциями |
нескольких |
переменны |
||||||||||
(аргументов). В данном пособии мы ограничимся рассмотрением случая двух |
||||||||||||||||||
независимых переменных, так как все основные свойства таких функций легко |
||||||||||||||||||
обобщить |
|
на |
|
большее |
число |
аргументов, |
кромеи |
того, функции |
двух |
|||||||||
переменных имеют вполне определенный геометрический смысл. |
|
|
|
|
||||||||||||||
Определение 1.1. |
Пусть D – некоторое множество упорядоченных |
|||||||||||||||||
пар действительных |
чисел(x; y) |
и |
пусть |
каждой |
|
паре(x; y) из D |
по |
|||||||||||
определенному правилу поставлено в соответствие единственное значение |
||||||||||||||||||
переменной |
z. |
Тогда |
говорят, что |
на |
множестве D |
задана функция |
двух |
|||||||||||
переменных |
|
z = f (x; y) . |
Переменные x и y называют независимыми |
|||||||||||||||
переменными (или аргументами), |
а переменную z – функцией. |
|
|
|
|
|||||||||||||
При |
нахождении |
частного |
значения |
функцииz = f (x; y) , |
которое |
она |
||||||||||||
принимает |
при |
|
конкретных значениях |
аргументовx = x0 , |
y = y0 , |
используют |
||||||||||||
обозначение |
z |
0 |
= f (x ; y ) . |
Например, если |
z = x2 + y2 |
+1 и x = 3, y |
0 |
= 4 , то |
||||||||||
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
||
z = 32 + 42 +1 = 26 .
Чтобы задать функцию двух переменных, следует задать способ, с помощью которого для каждой пары (x; y) из D можно найти соответствующее
значение |
функции. Чаще всего мы |
будем |
использовать |
способ |
|
задания с |
||||||||
помощью |
формулы z = f (x; y) , где |
f (x; y) – некоторое |
выражение, |
|||||||||||
зависящее |
от x |
и y. |
Например, z = |
|
|
|
Такой |
способ |
задания |
|||||
x2 + y2 |
-1 + ln(xy) . |
|||||||||||||
функции называется аналитическим. |
|
|
|
|
|
|
|
|
|
|
||||
Обычно функции двух переменных задаютаналитическим |
или |
|||||||||||||
табличным способами. Нас в дальнейшем будет интересовать аналитический |
||||||||||||||
способ задания, при котором функция задается некоторой формулой, |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
например, |
z(3; 4) = |
x2 + y2 -1 + ln(xy) . |
|
|
|
|
|
|
|
|
|
|||
Определение |
1.2. Множество |
всех |
пар ( |
x; у), при |
которых |
|||||||||
аналитическое выражение f (x; y) имеет |
смысл, называется |
областью |
||||||||||||
определения |
функции z = f (x; y) . |
В |
дальнейшем |
область |
определения |
|||||||||
функции будем обозначать символом |
D( f ) . |
|
|
|
|
|
|
|
|
|||||
4
Определение 1.3. Множество значений, принимаемых переменной z в области определения, называется множеством значений функции.
Так как каждой паре чисел(x; у) на координатной плоскости Oxy соответствует точка М с координатами (x; у), то для области определения
функции |
z = f (x; y) можно |
построить |
геометрическую модель: D( f ) |
– |
||
множество |
точек M (x; y) |
координатной плоскости, координаты которых |
||||
обеспечивают существование выраженияf (x; y) . Это |
может |
быть |
вся |
|||
координатная плоскость (например, D( f ) |
для функции z = x2 + y2 ) или часть |
|||||
плоскости, |
ограниченной |
некоторыми |
линиями. Эти |
линии |
называются |
|
границами области определения, а их точки – граничными точками области.
Точки области определения, не лежащие на границе, называются внутренними. Область, содержащая все свои граничные точки, называется замкнутой. Область, состоящая из одних внутренних точек, называется
открытой областью.
Отметим некоторые условия, которые используются при нахождении
областей определения функций, заданных аналитически: |
|
|
1) подкоренные выражения радикалов четных |
степеней должны быть |
|
неотрицательны, например для выражения |
φ(x; y) |
должно выполнятся |
неравенство φ(x; y) ³ 0 ; |
|
|
2) знаменатели дробей должны быть |
отличны от , нулят. е. для |
|
1 |
|
|
|
|
выражения φ(x; y) знаменатель φ(x; y) ¹ 0 ; |
|
|
||
3) выражение, стоящее |
под |
знаком |
логарифма |
должно |
положительно, например, для loga (φ(x; y)) должно выполняться условие
φ(x; y) > 0 ;
4) |
для выражений arcsin φ(x; y) , |
arccos φ(x; y) |
должно |
выполняться |
|||||||
условие -1 £ φ(x; y) £1; |
|
|
|
|
|
|
|||||
5) |
следует |
иметь в виду, что |
эти |
требования |
могут |
совмещаться. |
|||||
Например, |
если выражение имеет |
вид |
1 |
, то |
φ(x; y) > 0 . Для |
||||||
|
|||||||||||
φ(x; y) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
выражения |
1 |
|
|
должны |
|
выполняться |
|||||
|
|
|
|
|
|||||||
ln(φ(x; y))
быт
усло
φ(x; y) > 0; φ(x; y) ¹1 .
Определение |
1.4. Пусть функция |
двух |
переменных |
задана |
|||
аналитически |
формулой z = f (x; y) . |
Множество |
точек |
пространства, |
|||
координаты |
которых |
имеют вид(x; |
y; f(x; |
y)) таких, что (x; y) Î D( f ) , |
|
||
называется графиком |
функцииz = f (x; y) . В |
общем |
случае, |
графиком |
|
||
функции z = f (x; y) в |
заданной системе |
координат с областью определения |
|||||
D( f ) является некоторая поверхность. |
|
|
|
|
|
||
5

Рассмотрим примеры.
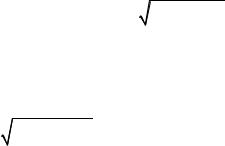
Пример 1.1. Найдите область определения функции двух переменных z( x; y) = 
 4 + y - x2 + ln( x2 -1) . Изобразите ее на чертеже.
4 + y - x2 + ln( x2 -1) . Изобразите ее на чертеже.
Решение. Областью определения функции является множество точек плоскости Оху, координаты которых удовлетворяют системе неравенств
ì |
+ y - x |
2 |
³ 0, |
ì |
|
2 |
- 4, |
(1.1) |
ï4 |
|
ïy ³ x |
|
|
||||
í |
2 -1 > 0. |
|
Û í |
>1. |
|
(1.2) |
||
ïx |
|
ïx2 |
|
|||||
î |
|
|
|
î |
|
|
|
|
Рассмотрим сначала |
|
неравенство (1.1). Ему будет |
соответствовать |
|||||
уравнение y = x2 - 4 , которое определяет параболу с вершиной в точке (0; - 4) , ветви ее направлены вверх. Парабола делит координатную плоскость на две части: внешнюю и внутреннюю. Для одной из нихy > x2 - 4 , для другой
y < x2 - 4 (на |
самой параболе y = x2 - 4 ). Чтобы |
установить, |
какая |
из |
этих |
|
частей |
состоит |
из точек, для которых y ³ x2 - 4 , |
достаточно |
проверить |
это |
|
условие |
для какой-нибудь одной точки. Возьмем, |
например, |
точку |
A(0; 1) . |
||
Подставив ее координаты в неравенство(1.1.), получим верное числовое
неравенство 1 ³ 0 - 4 . Значит |
эта точка и подобные ей(т. |
е. |
внутренние, |
||||
лежащие |
между ветвями |
параболы |
или на) даютней |
геометрическое |
|||
изображение |
области, |
определяемой |
неравенством (1.1). |
Рассмотрим |
|||
неравенство |
(1.2) |
x2 >1. |
Это |
неравенство |
равносильно совокупности двух |
||
неравенств x < -1 или x >1. Они определяют части плоскости, |
лежащие левее |
||||||
прямой x = -1 или правее прямой x =1, причем точки самих прямых в область определения не входят. В таком случае будем изображать соответствующие линии пунктиром. Областью определения функции будет множество точек плоскости, координаты которых удовлетворяют системе. Это будет параболическая зона, из которой удалены точки, лежащие между прямыми и на прямых x = -1, x =1. Точки параболы принадлежат области(см. рис. 1.1). На рисунке область определения заштрихована.
Рис. 1.1
6

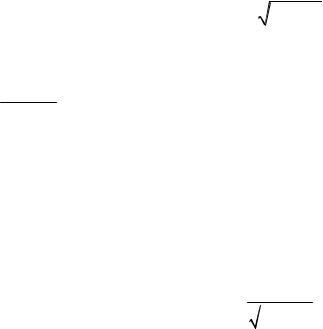
Пример 1.2. Найдите область определения функции двух переменных
z( x; y) = arcsin( y - x) + |
|
1 |
|
|
. Изобразите ее на чертеже. |
|
|
||||
|
|
|
|
|
|
|
|||||
1 - x2 - y 2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
Решение. Областью определения этой |
функции является |
множество |
|||||||||
точек плоскости Оху, значения |
координат |
которых удовлетворяют |
системе |
||||||||
неравенств |
|
|
|
|
|
|
|
|
|
|
|
ì-1 £ y - x £1, |
|
|
ìx -1 £ y £ x +1, |
|
(1.3) |
||||||
í |
|
|
|
или í |
x2 |
+ y |
2 <1. |
|
(1.4) |
||
1 - x2 |
|
- y2 > 0. |
î |
|
|||||||
î |
|
|
|
|
|
|
|
|
|
||
Решения двойного неравенства(1.3) изображаются на координатной |
|||||||||||
плоскости точками, лежащими |
на |
|
прямых |
y = x +1; =y x -1 |
и |
между |
|||||
ними. Решения неравенства (1.4) – точки внутренней части круга, с центром в начале координат и радиуса 1. Таким образом, область определения данной функции − множество точек полосы, лежащих внутри окружности x2 + y2 =1.
Границы полосы − прямые y = x -1 и y = x +1. На чертеже (см. рис. 1.2) область определения заштрихована.
Рис. 1.2
2. Линии уровня функции
Определение 2.1. Линии на плоскости Оху, уравнения которых имеют
вид f(x; y) |
= С, называются линиями уровня функции двух переменных |
z = f (x; y) . |
|
Построение линий уровня, соответствующих различным значениям |
|
постоянной |
величины С, позволяет увидеть характер поверхности, заданной |
исследуемой функцией.
7
Сгущение линий уровня означает более быстрое изменение значений
функции. Редкое |
расположение |
линий |
уровня |
характеризует |
пологую |
поверхность (т. е. значения функции изменяются медленно). |
|
|
|||
Линии равных высот на физической карте – это пример линий уровня. |
|
||||
Пример 2.1. Найдите линии уровня функции z = f (x; y) = ex+y . |
|
||||
Решение. Линии уровня функции |
z(x; y) = ex+ y – это семейство линий на |
||||
плоскости Оху, описываемое уравнением ex+ y = C . Представим это уравнение в другой форме, выполнив следующие преобразования:
ex+ y = C =или ex+ y eln C , значит x + y = ln C.
Пусть ln C = C* , тогда x + y =C*, =y C* - x (семейство прямых линий). Они показаны на рис. 2.1.
|
|
|
Рис. 2.1 |
|
|
|
|
|
Пример 2.2. Найдите линии уровня функции z(x; y) = |
|
|
|
|
|
|||
|
y - x2 . |
|
||||||
|
|
|
|
|
|
|||
Решение. Определить линии уровняфункции z(x; y) = |
|
y - x2 |
как |
|||||
семейства |
кривых y = g(x;C) на плоскости Оху |
можно, |
осуществляя |
|||||
следующие преобразования: |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
y - x2 = C или y - x2 = C2. |
|
|
|
|
|
|
Пусть C 2 |
= C* , тогда y - x2 = C* , где C* ³ 0 , (семейство парабол y = x2 + C* ). |
|||||||
Они показаны на рис. 2.2.
8
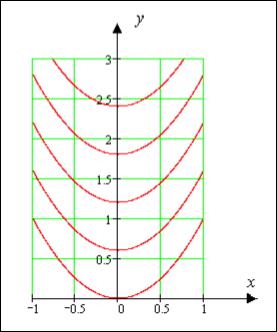
Рис. 2.2
3. Предел и непрерывность функции двух переменных
Определение |
3.1. |
δ-окрестностью |
точки Р0(х0;у0) |
называется |
||
внутренность круга радиуса δ с центром в этой точке. |
|
|||||
Определение |
3.2. |
Число |
А |
называется пределом |
функции |
|
z = f (x; y) = f (P) при P ® P0 , если |
для |
любого |
положительного |
числаe > 0 |
||
найдется такая δ-окрестность точки P0 ( x0 ; y0 ) , что для любой точки P (x ; y ) из этой окрестности (за исключением может быть точкиP0 ( x0 ; y0 ) ) выполняется
неравенство |
f (P) - A |
|
< e . При этом пишут: lim f (P) = A или lim f (x, y) = A . |
|
|
|
|
P®P0 |
x®x0 |
|
|
|||
|
|
|
|
y® y0 |
Геометрический смысл предела функции двух переменных состоит в том, |
||||
что каково |
бы ни было числоe > 0 , найдется |
такая δ-окрестность точки |
||
P0 ( x0 ; y0 ) , что во всех точках P (x ; y) этой окрестности, отличных от P0 (x0 ; y0 ) , аппликаты соответствующих точек поверхности z = f ( x; y) отличаются от числа
А по модулю меньше, чем на e . |
|
|
||
Определение 3.3. Функция |
z = f ( x; y) |
называется непрерывной в точке |
||
P0 ( x0 ; y0 ) , если она: |
|
|
||
1) |
определена в этой точке и некоторой ее окрестности; |
|||
2) |
имеет предел в этой точке |
lim f (P) ; |
|
|
|
|
|
P®P0 |
|
3) |
этот предел равен значению функции |
z = f ( x; y) в точке P0 ( x0 ; y0 ) , |
||
|
т.е. |
lim f (P) = f (P0 ) . |
|
|
|
|
P®P0 |
|
|
9
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области.
Точки, в которых непрерывность нарушается, т. е. не выполняется хотя бы одно из условий непрерывности, называются точками разрыва
этой |
функции. |
Точки |
разрыва функции z = f ( x; y) |
могут |
образовывать |
||
целые |
линии |
разрыва. |
Так, например, функция z = |
2 |
|
имеет линию |
|
y - x |
|||||||
|
|
|
|
|
|||
разрыва y = x .
4. Дифференцирование функции двух переменных
|
|
Определение |
4.1. |
Разность |
f (x0 + Dx; y0 ) - f (x0 ; y0 ) |
называется |
||||
частным |
приращением |
функции z = f ( x; y) |
по |
переменнойх |
в |
точке |
||||
P0 |
( x0 |
; y0 ) . Обозначение: Dx z f=(x0 + Dx; y0 ) - f (x0 ; y0 ) . |
|
|
||||||
|
|
Определение |
4.2. |
Разность |
f (x0; y0 + Dy) - f (x0 ; y0 ) |
называется |
||||
частным |
приращением |
функции z = f ( x; y) |
по |
переменнойy |
в |
точке |
||||
P0 |
( x0 |
; y0 ) . Обозначение: Dy z = f (x0 ; y0 + Dy) - f (x0 ; y0 ) . |
|
|
||||||
Определение 4.3. Предел отношения частного приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю, называется частной производной функции z = f ( x; y) по одному из ее аргументов:
|
¶z |
|
= lim |
Dx z |
|
|
|
¶z |
= lim |
|
D y z |
|
|
|
|
|
|
¶x |
Dx , |
|
¶y |
|
Dy . |
|
|
|
|
||||||
|
Dx®0 |
|
Dy®0 |
|
|
|
|
|
||||||||
Используются также обозначения: |
z¢x , z¢y , |
f x¢, f y¢ . |
|
|
|
|
||||||||||
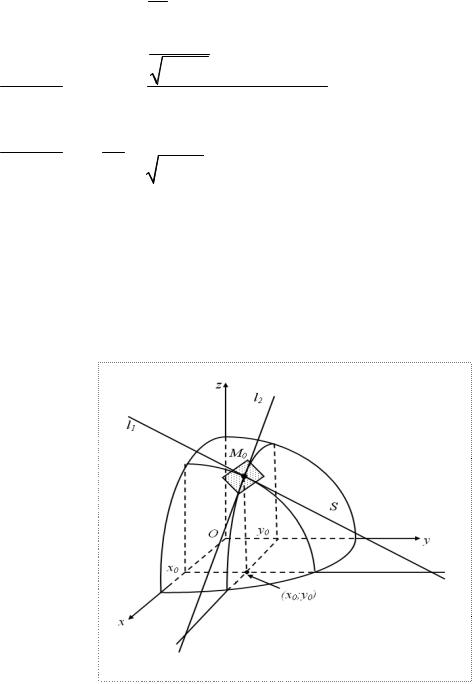
Геометрический смысл частных производных z¢x и z¢y |
заключается в том, |
|||||||||||||||
что они равны значениям |
угловых |
коэффициентов |
касательныхl и |
l |
2 |
к |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
линиям пересечения поверхности, определяемой |
|
уравнением z = f (x; y) , |
||||||||||||||
плоскостями x = x0 , y = y0 , |
проходящими |
|
через |
точку |
0М(касательная l1 |
|||||||||||
параллельна плоскости Oxz, касательная |
l2 |
параллельна плоскости Oуz) |
–(см. |
|||||||||||||
рис. 4.1). |
|
|
|
|
|
в точке P0 соответственно равны |
||||||||||
Значения частных производных zx¢ |
и z¢y |
|
||||||||||||||
z¢x (x0 ; y0 ) = tgα и z¢y (x0 ; y0 ) = tgβ .
10
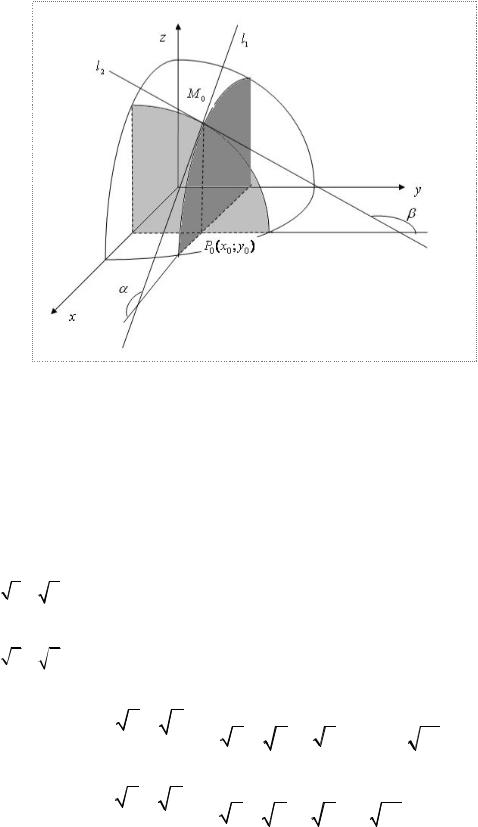
Рис. 4.1
Частная производная функции двух переменных по переменнойх представляет собой обыкновенную производную функции одной переменной при фиксированном значении у, поэтому ее находят по правилам вычисления производных функций одной переменной (аналогично рассматривается и частная производная по переменной у).
Пример |
4.1. |
Найдите частные производныеz¢x |
и |
z¢y |
функции |
|||||
z(x; y) = ln ( |
|
+ |
|
). |
|
|
|
|
|
|
x |
y |
|
|
|
|
|
||||
Решение. |
|
|
Найдем частные |
производные z¢x |
и |
z¢y |
функции |
|||
z( x; y) = ln (
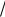 x +
x + 
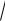 y ):
y ):
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
||||||
z¢x = |
(ln ( x + y ))= |
|
|
|
|
× |
|
|
|
= |
|
. |
|||||||||||||||||||||||||
|
¶x |
|
|
|
|
+ |
|
|
|
|
|
|
2 |
|
|
|
|
|
2x + 2 |
|
|
||||||||||||||||
|
x |
y |
x |
xy |
|||||||||||||||||||||||||||||||||
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|||||
z¢y = |
|
(ln ( x + y ))= |
|
|
|
|
|
|
× |
|
|
|
= |
|
|
|
|
. |
|||||||||||||||||||
¶y |
|
|
|
|
+ |
|
|
|
|
2 |
|
|
|
2 |
|
+ 2 y |
|||||||||||||||||||||
|
|
x |
y |
y |
xy |
||||||||||||||||||||||||||||||||
Пример |
4.2. |
|
Найдите частные |
|
|
производныеz¢x и z¢y функции |
|||||||||||||||||||||||||||||||
æ y |
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z(x, y) = arctgç |
|
+ 1÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
è x |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11

Решение. |
Найдем |
частные |
производныеz¢ |
и |
z¢ |
функции |
||
|
|
|
|
|
x |
|
y |
|
æ y |
|
ö |
|
|
|
|
|
|
z(x, y) = arctgç |
|
+1÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
è x |
|
ø |
|
|
|
|
|
|
z¢x |
|
|
¶ æ |
æ y |
|
|
öö |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
¶ |
|
æ y |
ö |
|
||||||||||||||
= |
|
|
|
|
çarctgç |
|
|
|
+1÷÷= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
ç |
|
|
+1÷ |
= |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ y |
|
ö |
2 |
¶x |
|
|
|||||||||||||||||||||||
|
|
|
¶x è |
è x |
|
|
øø |
|
|
|
|
|
|
|
|
|
|
|
|
|
è x |
ø |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + |
ç |
|
|
|
+1÷ |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è x |
|
ø |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
æ |
|
|
|
1 |
|
ö |
|
|
|
|
|
|
|
|
|
|
-x2 y |
|
|
||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
× y ç |
- |
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1+ |
( y + x) |
|
|
|
|
è |
|
|
|
x2 |
ø |
|
|
|
(x2 + y2 + 2 yx + x2 )x2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z¢y |
|
|
¶ æ |
æ y |
|
|
öö |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
¶ æ y |
|
|
ö |
|
||||||||||||||||
= |
|
|
|
|
çarctgç |
|
|
|
+1÷÷= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× |
|
|
ç |
|
|
|
+1÷ = |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ y |
|
|
ö |
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
¶y è |
è x |
|
|
øø |
|
|
|
|
|
|
|
|
|
|
|
|
|
¶y è x |
|
|
ø |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
ç |
|
|
|
+1÷ |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è x |
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|||
|
= |
|
|
|
|
|
x2 |
|
|
|
|
× |
1 |
|
×1 |
= |
|
|
|
|
|
|
|
x |
|
|
|
|
|
. |
|
|
|
|
|||||||||
|
|
|
2x2 + 2 yx + y2 |
x |
2x2 + 2yx + y2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
-y
2x2 + 2 yx + y2 . =
5. Дифференцирование неявных функций двух переменных
Пусть некоторая функция z = f (x; y) |
задана уравнением F (x; y; z) = 0 . |
|
|
|
||||||||||||||||||||||
Справедлива теорема (о |
существовании |
неявной |
функции): если |
функция |
||||||||||||||||||||||
F (x; y; z) и |
|
ее |
|
частные |
|
|
|
|
|
¢ |
(x; y; z) , |
¢ |
(x; y; z) |
|
¢ |
|
|
|
|
|||||||
|
|
производныеF |
F |
и F (x; y; z) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
z |
|
|
|
|
|
определены |
и |
непрерывны |
в |
|
некоторой |
окрестности |
точкиM (x ; y |
; z |
0 |
) ; |
||||||||||||||||
причем |
F (x0 ; y0 ; z0 ) = 0 , а |
Fz¢(x0 ; y0 ; z0 ) ¹ 0 , |
|
|
|
|
0 |
0 |
0 |
|
|
|||||||||||||||
то |
существует окрестность |
точки |
||||||||||||||||||||||||
M 0 , в |
которой |
уравнение F (x; y; z) = 0 |
определяет |
единственную |
|
функцию |
||||||||||||||||||||
z = f (x; y) , непрерывную и дифференцируемую в окрестности точки (x0 ; y0 ) . |
|
|||||||||||||||||||||||||
Пусть |
условия теоремы |
|
|
выполняются для некоторой функции, тогда |
|
|
ее |
|||||||||||||||||||
частные производные могут быть найдены по формулам |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
z¢x |
|
|
F |
¢(x; y; z) |
, z¢y |
|
|
Fy¢(x; y; z) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
= - |
=x |
|
|
- |
|
|
|
|
. |
|
|
|
|
(4.1) |
|||||||||
|
|
|
|
|
Fz¢(x; y; z) |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Fz¢(x; y; z) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 4.1. Найдите частные производные функции z = f (x; y) , заданной |
|
|
|
|||||||||||||||||||||||
неявно уравнением |
sin z - z2 + 2xy + y2 = 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Решение. Находим частные производные и подставляем их в формулы (4.1). |
|
|
||||||||||||||||||||||||
Получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
¢ |
|
cos z - 2z , |
|
|
|
|
|
||
|
F |
(x; y; z) = 2 y, F=(x; y; z) |
|
2x + 2 y, F=(x; y; z) |
|
|
|
|
|
|||||||||||||||||
|
x |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
z¢x |
= |
|
|
2 y |
|
, z¢y |
= |
2x + 2 y |
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2z |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
- cos z |
|
|
|
2z - cos z |
|
|
|
|
|
|
|
|
|
|
|||||||
12

Пример 4.2. Найдите частные производные функции z = f (x, y) , если она
задана неявно уравнением x + ln z + e2 x+z - xy2 = 0 . y
Решение. Находим частные производные и подставляем их в формулы (4.1). Получим
Fx¢(x, y, z) = |
1 |
+ 2e2x+z - y2 ,=Fy¢(x, y, z) - |
(x + ln z) |
- 2xy=, Fz¢(x, y, z) |
1 |
+ e2 x+z , |
||||||||||||
|
|
|
y2 |
|
||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
yz |
||||||
|
|
|
|
1 |
+ 2e2x+z - y2 |
|
- |
(x + ln z) |
- 2xy |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
z¢x = |
|
y |
, z¢y = |
|
|
|
y2 |
|
|
. |
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
+ e2 x+z |
|
|
|
|
+ e2 x+z |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
yz |
|
|
|
|
yz |
|
|
|
|
|
||
6. Полный дифференциал функции
Определение 6.1. Полным приращением функции z = f ( x; y ) в точке
P0 ( x0 ; y0 ) называется разность Dz = f (x0 + Dx; y0 + Dy) - f ( x0 ; y0 ) . Определение 6.2. Функция z = f (x; y) называется дифференцируемой
вточке P(x; y) , если ее полное приращение в этой точке может быть
представлено в виде Dz = ADx + BDy + α(Dx; Dy) , где А и В – не зависят от ∆х и
∆у, а α(Dx; Dy) – бесконечно малая величина, для которой lim |
α(Dx; Dy) |
|
|
= 0 . |
|||
|
|
|
|
|
|
||
|
Dx |
2 |
+ Dy |
2 |
|||
Dx®0 |
|
|
|
||||
Dy®0 |
|
|
|
|
|
||
Определение 6.3. Главная, линейная относительно ∆х |
и ∆у |
|
|
часть |
|||
приращения функции, называется полным дифференциалом |
этой функции и |
||||||
обозначается dz: |
|
|
|
|
|
|
|
dz = ADx + BDy . |
|
|
|
|
|
|
|
Можно показать, что для дифференцируемой функции A = ¶z ; B = ¶z .
|
|
|
¶x |
|
|
¶y |
Поскольку приращения независимых переменныхx и |
y совпадают с их |
|||||
дифференциалами Dx = dx, Dy = dy , окончательно имеем |
dz = |
¶z |
dx + |
¶z |
dy . |
|
|
|
|||||
|
|
¶x |
|
¶y |
||
Геометрический смысл дифференциала dz функции z = f (x; y) |
состоит в |
|||||
том, что он равен приращению Dz аппликаты касательной плоскости.
Пример. Найдите полный дифференциалdz функции двух переменных
z(x; y) = x arcsin y . y
Решение. Полный дифференциал dz функции z(x; y) = xarcsin y равен y
13
æ x arcsin y ö |
¶ |
æ x arcsin y ö |
¶ æ x arcsin y ö |
|||||||
dz = d ç |
|
÷ |
|
=ç |
|
÷dx + |
|
ç |
|
÷dy = |
y |
|
y |
|
y |
||||||
è |
ø |
¶x è |
ø |
¶y è |
ø |
|||||
=arcsin y ×1× dx + y
=arcsin y dx + x y 2y
x ×
æ
×ç
ç
è
1
× y - arcsin y ×1
1 - y2
y2
dy =
|
y |
|
|
|
ö |
|
|
|
- arcsin y |
÷ |
|
|
|
|
|
||
1 - y |
2 |
|
÷dy. |
||
|
|
|
ø |
||
7. Касательная плоскость и нормаль к поверхности
Пусть |
функция z = f ( x; y) дифференцируема |
в |
точкеP |
(x ; y |
0 |
) |
|
области D , лежащей в плоскости Oxy . Рассечем |
0 |
0 |
|
||
некоторой |
поверхность S, |
|||||
изображающую функцию z, плоскостями x = x0 , y = y0 (см. рис. 7.1). |
|
|
|
|||
|
|
x = x0 |
|
|
Рис. 7.1. |
|
|
|
|||
Плоскость |
пересекает поверхностьS по некоторой |
линии, |
|||||||||
уравнение |
которой |
в |
плоскостиx = x0 |
имеет |
видz = f (x0 ; y) = φ1 ( y) . |
Оно |
|||||
получается |
подстановкой x = x0 |
в исходную |
функциюz = f ( x; y) . |
Точка |
|||||||
M 0 (x0 ; y0 ; f (x0 ; y0 )) |
принадлежит кривой φ ( y) , лежащей в плоскости x = x . В |
||||||||||
|
|
|
|
|
функцииz |
1 |
точкеМ0 функция φ1 ( y) |
|
0 |
||
силу дифференцируемости |
в |
|
также |
||||||||
является дифференцируемой |
в |
точкеy = y0 . |
Следовательно, в этой |
точке в |
|||||||
плоскости x = x0 |
к кривой |
φ ( y) может быть проведена касательная l1. |
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
14

|
|
|
|
y = y |
Проводя аналогичные рассуждения для сечения плоскостью0 , |
||||
построим касательную l2 |
к кривой z = f (x; y ) = φ |
2 |
(x) в точке x = x0 . Прямые |
|
|
|
0 |
|
|
l1 и l2 |
определяют |
плоскость(α) , которая |
|
называется касательной |
плоскостью к поверхности S в точке М0.
Можно показать, что уравнение касательной плоскости в точкеM 0 к
поверхности S имеет следующий вид: |
|
|
|
z - z0 = |
f x¢(x0 ; y0 )×(x - x0 )+ f y¢(x0 ; y0 )×(y - y0 ). |
( 7.1) |
|
Прямая, проходящая через точкуМ0 |
и перпендикулярная касательной |
||
плоскости, построенной в этой точке поверхности, называется |
нормалью к |
||
поверхности S в точке M 0 . |
|
|
|
Нормальный |
вектор касательной |
плоскости может |
быть принят за |
направляющий вектор нормали к поверхности, поэтому ее канонические уравнения будут
|
|
|
|
|
x - x0 |
|
= |
|
|
|
y - y0 |
|
|
= |
|
z - z0 |
. |
|
|
|
(7.2) |
||||||
|
|
|
|
f x¢(x0 ; y0 ) |
|
|
f y¢(x0 ; y0 ) |
-1 |
|
|
|
||||||||||||||||
Если поверхность задана уравнением F (x; y; z) = 0 , то уравнения |
|
||||||||||||||||||||||||||
касательной плоскости и нормали будут соответственно |
|
|
|
|
|||||||||||||||||||||||
Fx¢(M 0 )( x - x0 ) + Fy¢(M 0 )( y - y0 ) + Fz¢(M 0 )( z - z0 ) = 0 . |
|
|
|
(7.3) |
|||||||||||||||||||||||
|
|
x - x |
0 |
= |
y - y |
0 |
|
|
= |
|
z - z |
0 |
. |
|
|
|
|
|
|
(7.4) |
|||||||
|
|
¢ |
(M 0 ) |
¢ |
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|||||||||
|
|
Fx |
|
Fy |
(M 0 ) |
|
Fz (M 0 ) |
|
|
|
|
|
|
|
|||||||||||||
Пример 7.1. Составьте уравнения касательной плоскости и нормали к |
|||||||||||||||||||||||||||
поверхности z = x2 + y2 -1 в точке M0 (1; -2;4) . |
|
|
¢ |
|
z |
¢ |
|
||||||||||||||||||||
Решение. |
Найдем |
|
значения |
|
|
|
|
|
|
|
|
|
и |
данной |
|||||||||||||
|
|
частных производныхz |
y |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
функции в точке |
(1; -2) : |
|
|
|
|
|
|
|
|
|
|
|
(1; |
-2) = -4. |
|
|
|
|
|
||||||||
¢ |
¢ |
|
|
|
|
|
¢ |
|
2 y, |
¢ |
|
|
|
|
|
||||||||||||
zx = 2x, zx (1; -2) = 2, =zy |
|
|
zy |
|
|
|
|
|
|||||||||||||||||||
Уравнение |
касательной |
плоскости |
|
к |
поверхностиz(x; y) = x2 + y2 -1, в |
||||||||||||||||||||||
точке M 0 будет |
|
|
|
|
|
z - 4 |
|
2(= x -1) - 4( y + 2) или |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2x - 4 y - z - 6 = 0.
Используя равенства (7.2), получим канонические уравнения нормали:
x -1 = y + 2 = z - 4 .
2 -4 -1
Пример 7.2. Составьте уравнения касательной плоскости и нормали к поверхности x2 + y2 - z2 = -1 в точке M 0 (2; 2; 3) .
15

Решение. Чтобы записать уравнение касательной плоскости и нормали к поверхности, определяемой заданной функцией, найдем значения частных производных от этой функции в точке M 0 :
Fx¢ = 2x , F¢(M |
0 |
) = 2 ×2 = 4 ; |
||||
|
|
|
x |
|
|
|
Fy¢ = 2 y , F ¢(M |
0 |
) = 2 × 2 = 4 ; |
||||
|
|
|
y |
|
|
|
F |
¢ |
= -2z , |
¢ |
|
|
= - × = - . |
z |
|
Fz (M0 ) |
2 3 6 |
|||
Запишем уравнение касательной плоскости |
||||||
4(x - 2) + 4( y - 2) - 6( z - 3) = 0 |
или после преобразований 2x + 2 y - 3z +1 = 0 , |
|||||
Канонические уравнения нормали будут иметь вид x - 2 = y - 2 = z - 3 .
4 4 6
8. Производная по направлению и градиент функции
|
Пусть |
функция z = f ( x; y) определена |
в некоторой окрестности |
точки |
|||||||||||||||||||||||||
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М0(х0;у0), |
а |
l |
– данное |
|
направление, |
задаваемое |
единичным |
|
вектором |
||||||||||||||||||||
e = {cos α;cosβ}, |
|
r |
|
= cos2 α + cos2 β =1, при этом α + β = π , а |
cosα |
и |
cosβ – |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
e |
|
|||||||||||||||||||||||||||
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
косинусы |
углов, |
образуемых |
|
с |
осями |
|
|
|
|
|
|||||||||||||||||||
вектором l |
координат(направляющие |
||||||||||||||||||||||||||||
косинусы). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точки |
|||
|
Определение 8.1. При перемещении в данном направленииl |
||||||||||||||||||||||||||||
М0(х0;у0) в |
точку M1 (x0 + Dx,; y0 + Dy) |
|
|
|
функция z = f ( x; y) |
получает |
|||||||||||||||||||||||
приращение |
|
|
Dl=z(x0 ; y0 ) |
f (x0 + Dx; y0 + Dy) - f (x0 ; y0 ) , |
называемое |
||||||||||||||||||||||||
приращением функции z = f (x; y) в данном направлении. |
|
|
|
|
|||||||||||||||||||||||||
|
Длина |
отрезка M 0 M1 |
|
uur |
численно |
равна гипотенузе |
прямоугольного |
||||||||||||||||||||||
|
= |
Dl |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uur |
|
|
|
треугольника, катеты которого |
равны Dx и Dy , следовательно, |
Dx = |
×cos α , |
||||||||||||||||||||||||||
Dl |
|||||||||||||||||||||||||||||
|
uur |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dy = |
×cos β |
и приращение функции Dl z(x; y) в данном направлении можно |
|||||||||||||||||||||||||||
Dl |
|||||||||||||||||||||||||||||
представить следующей формулой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
Dl =z(x0 ; y0 ) |
f (x0 + |
uur |
|
|
y0 + |
uur |
cos β) - f (x0 ; y0 ) . |
|
|
|
|||||||||||||||
|
|
|
|
Dl |
cos α; |
|
Dl |
|
|
|
|||||||||||||||||||
|
Если рассматривать произвольную точку M (x; y) , то можно ввести такое |
||||||||||||||||||||||||||||
определение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Определение 8.2. Производной zl¢(x; y) по направлению l |
функции |
|||||||||||||||||||||||||||
двух переменных z = f ( x; y) называется |
|
|
предел |
отношения |
приращения |
||||||||||||||||||||||||
функции в этом направлении к величине приращения |
uur |
|
при стремлении |
l к |
|||||||||||||||||||||||||
Dl |
|
||||||||||||||||||||||||||||
нулю: |
|
|
|
|
|
|
|
|
|
|
|
|
D z(x; y) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
zl¢(x; y) = lim |
|
. |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
uur |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Dl®0 |
|
Dl |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
16

Производная по направлению zl¢(x; y) характеризует скорость изменения
функции |
z = f ( x; y) |
в |
направленииl |
и |
|
|
определяется |
|
выражением: |
|||
zl¢(x; y) = z¢x |
× cos α + z¢y ×cosβ , |
где cos α , cos β – направляющие косинусы вектора |
||||||||||
|
|
|
|
|
lx |
|
|
ly , где |
r |
|
||
l , которые вычисляются |
по формулам |
|
, |
|
l – |
вектор, |
||||||
|
|
|
cos α = |
r |
|
cos β = |
|
r |
|
|
|
|
|
|
|
|
|
l |
|
|
|
l |
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
= lx2 + ly2 – модуль |
||||
задающий данное направление, lx , ly - его координаты, а |
|
l |
|
||||
r |
|
|
|
|
|
|
|
|
|
|
|
||||
вектора l . |
|
|
|||||
Пример 8.1. Вычислите производную функции z(x; y) = 5x4 |
- 3x - y -1 |
||||||
uuuuuur |
|
|
|||||
в точке M 0 (2;1) по направлению вектора M 0 M1 , где M1 (5;5) . |
|
|
|||||
Решение. Нахождение производнойzl¢(x0 ; y0 ) по направлению вектора |
|||||||
uuuuuur |
|
|
|||||
M 0 M1 согласно формуле zl¢(x; y) = z¢x × cos α + z¢y × cos β связано с |
определением |
||||||
частных производных z¢x , z¢y и направляющих косинусов cos α, cos β.
Вычислим частные производные |
z¢x и z¢y в точке M 0 (2; 1) : |
||||
z¢x |
= |
¶ |
|
(5x4 - 3x - y -1)= 20x3 |
- 3, z¢x (2; 1) = 20 × 23 - 3 = 157, |
|
|||||
|
|
¶x |
|
||
z¢y |
= |
¶ |
(5x4 - 3x - y -1)= -1, |
z¢y (2; 1) = -1. |
|
|
|||||
|
|
¶y |
|
||
Направляющие косинусы cosα и cosβ можно найти, если использовать uuuuuur
приведенные выше формулы. M 0M1 = {5 - 2;5 -1} = {3; 4},
|
uuuuuur |
|
|
|
|
|
|
5=. Тогда |
cos α = |
3 |
, cosβ |
= |
4 |
. |
|
|
|
|
|
|||||
|
M0 M1 |
= 32 + 42 |
|
= 25 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
5 |
5 |
uuuuuur |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Значение производной функции z по направлению M 0 M1 |
в точке |
|||||||||||||||||||||
|
M 0 (2;1) равно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
4 |
|
|
||||
|
|
|
z¢(2;1) = z¢ |
(2;1) ×cos α + z¢ (2;1) ×cosβ |
157= |
× |
+ (-1) × |
|
93, 4=. |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
l |
|
|
x |
|
|
|
y |
|
|
|
|
|
|
5 |
|
5 |
|
|
|||
Так как z¢(2; 1) |
в точке M |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
(2;1) положительна, то можно сделать вывод, что |
|||||||||||||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
uuuuuur |
|
|
|
||||||
функция z( x; y) возрастает в направлении вектора M 0 M1 . |
|
|
|
|||||||||||||||||||||
|
|
Определение 8.3. Градиентом grad z |
функции z = f ( x; y) называется |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
¢ |
|
¢ |
|
|
¢ |
|
¢ |
|
|
|
|
|
|
|
||
вектор с координатами zx |
; zy , т. е. grad z |
= {zx |
; zy }. |
|
|
|
|
|
|
|||||||||||||||
|
|
Легко видеть, что производная по направлениюzl¢ равна скалярному |
||||||||||||||||||||||
произведению |
градиента |
функцииz |
и |
|
единичного |
|
вектора, задающего |
|||||||||||||||||
направление вдоль некоторой прямой l , т. е. |
¶z |
|
|
|
|
r |
z¢x cos= α + z¢y cosβ . |
|||||||||||||||||
|
|
= grad z ×e |
||||||||||||||||||||||
¶l |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
17

Градиент функции z = f ( x; y) в данной точке характеризует направление
максимальной скорости изменения функции в этой точке. |
|
|
|
|
|||||||||||||||
Пример 8.2. Найдите |
градиентgrad z |
функции |
z = x × ln(x + y) |
и его |
|||||||||||||||
модуль в точке M 0 (-1;2) . |
вектораgrad z |
|
|
|
|
|
|
||||||||||||
Решение. |
Координаты |
можно |
найти, если |
вычислить |
|||||||||||||||
значения частных производных z¢x и z¢y в точке M 0 (-1;2) : |
|
|
|
|
|||||||||||||||
|
¢ |
|
¶ |
|
|
|
|
|
|
|
|
|
|
¢ |
|
x |
|
|
|
z |
= |
¶x ( |
x ×ln (x + y)= 1×ln(x + y) + x × |
|
|
|
|
, |
|
||||||||||
|
(ln(x + y))= ln(x + y) + |
|
|
||||||||||||||||
|
x |
|
|
) |
|
|
|
|
|
|
|
x |
|
x + y |
|
||||
z¢x (-1;=2) |
ln1 -1= -1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
z¢y |
= |
¶ |
(x ×ln(x + y)) =x × (ln(x + y))¢y = |
|
x |
, |
|
|
|
|
|
||||||||
¶y |
|
x + y |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z¢y (-1;=2) -1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда grad z = {-1;-1}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Модуль градиента функции |
|
grad z |
|
|
|
в точке M 0 (-1;2) – это длина |
этого |
||||||||||||
|
|
|
|||||||||||||||||
вектора:
grad z = 
 (z¢x (-1; 2))2 + (z¢y (- 1; 2))2 =
(z¢x (-1; 2))2 + (z¢y (- 1; 2))2 = 
 (-1 2) + -(1 2 =)
(-1 2) + -(1 2 =) 
 2.
2.
9. Частные производные второго порядка
Определение 9.1. Частная производная от частной производной функции называется частной производной второго порядка.
Приняты следующие обозначения для частных производных второго порядка:
¶ æ |
|
¶z ö |
¢¢ |
= |
¢¢ |
(x; y) |
|
|
|
|
|
|
|||||||||
|
|
|
ç |
|
|
|
|
|
|
|
– функция |
дифференцируется |
|
пох |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
¶x |
|
|
|
|
÷ = z xx |
f xx |
|
|
||||||||||||
|
è |
|
¶x ø |
|
|
|
|
|
|
|
|
|
|
||||||||
последовательно два раза; |
|
|
|
|
|
|
|||||||||||||||
|
¶ æ |
|
¶z ö |
¢¢ |
= |
¢¢ |
(x; y) – |
|
|
|
|
|
|||||||||
|
|
|
|
ç |
|
|
|
|
|
функция |
сначала |
дифференцируется |
пох, |
а |
|||||||
|
|
|
|
|
|
|
÷ = zxy |
f xy |
|||||||||||||
|
|
¶y è |
|
¶x ø |
|
|
|
|
|
|
|
|
|
|
|||||||
результат дифференцируется по у; |
|
|
|
|
|||||||||||||||||
¶ |
æ |
|
ö |
|
|
|
|
|
|
|
|
|
|
||||||||
ç |
¶z |
÷ |
¢¢ |
= |
¢¢ |
(x; y) – |
функция |
сначала |
дифференцируется |
поу, |
а |
||||||||||
|
|
|
|
||||||||||||||||||
|
¶x |
ç |
|
÷ |
= z yx |
f yx |
|||||||||||||||
|
è |
¶y ø |
|
|
|
|
|
|
|
|
|
|
|||||||||
результат дифференцируется по х; |
|
|
|
|
|||||||||||||||||
¶ |
æ |
|
¶z ö |
= z¢¢ |
= f ¢¢ |
(x; y) |
|
|
|
|
|
|
|||||||||
|
|
|
|
ç |
|
|
÷ |
– |
функция |
дифференцируется |
|
упо |
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
¶y |
ç |
|
÷ |
yy |
|
yy |
|
|
||||||||||||
|
è |
|
¶y ø |
|
|
|
|
|
|
|
|
|
|
||||||||
последовательно два раза.
Теорема 9.1. Если функция z(x; y) дважды дифференцируема в точке
M 0 ( x0 , y0 ) , то ее смешанные производные z¢xy¢ и z¢yx¢ в этой точке равны.
18
Пример. Найдите частные производные второго порядка от функции z( x, y) = x 4 y 2 + x2 y - 3xy - 2 y .
Решение. Первоначально находим частные производные z¢x и z¢y :
|
z¢x = |
|
¶ |
|
(x4 y 2 + x2 y - 3xy - 2 y )= 4x3 y2 + 2xy - 3y, |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
z¢y = |
|
¶ |
|
(x4 y2 + x2 y - 3xy - 2 y)= 2x4 y + x2 - 3x - 2. |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Последовательно находим частные производные второго порядка: |
|||||||||||||||||||||||||||||
|
|
|
|
|
¶ |
|
|
|
3 |
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||
|
¢¢ |
= |
|
|
|
|
|
|
(4x y |
|
|
+ 2xy - 3y ) |
12=x y + 2 y, |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
zxx |
|
¶x |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
¶ |
|
|
|
3 |
2 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||
|
¢¢ |
|
|
|
|
|
|
|
|
|
(4x y |
|
+ 2xy - 3y )= 8x y + 2x - 3, |
|
|
|
||||||||||||||
|
= ¶y |
|
|
|
|
|||||||||||||||||||||||||
|
zxy |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
¶ |
|
|
|
|
4 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|||||
|
¢¢ |
= |
|
|
|
|
|
|
|
(2x y |
|
+ x - 3x - 2) =8x y + 2x - 3, |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
zyx |
|
|
¶x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
¶ |
|
|
|
4 |
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||
|
¢¢ |
= |
|
|
|
|
|
|
(2x y |
+ x - 3x - 2) = 2x . |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
zyy |
|
|
¶y |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10. Экстремум функции |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Определение 10.1. Точка |
P0 (x0 ; y0 ) |
называется точкой максимума |
|||||||||||||||||||||||||||
функции z = f (x; y) , а значение функции в ней z0 |
= f (x0 ; y0 ) |
– максимумом, |
||||||||||||||||||||||||||||
если существует такая окрестность этой точки, что для всех |
точек P(x; y) из |
|||||||||||||||||||||||||||||
этой |
|
окрестности, |
|
отличных |
от P0 ( x0 ; y0 ) , |
выполняется |
неравенство |
|||||||||||||||||||||||
f (x; y) < f (x0 ; y0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Определение 10.2. Точка |
P0 (x0 ; y0 ) |
называется точкой |
минимума |
||||||||||||||||||||||||||
функции z = f ( x; y) , |
|
а значение функции в ней z0 = f ( x0 ; y0 ) |
– минимумом, |
|||||||||||||||||||||||||||
если существует такая окрестность этой точки, что для всех точек P (x ; y ) из |
||||||||||||||||||||||||||||||
этой |
окрестности, |
отличных |
от P0 ( x0 ; y0 ) , |
выполняется |
неравенство |
|||||||||||||||||||||||||
f (x; y) > f (x0 ; y0 ) . |
|
|
Максимум |
и |
|
|
|
минимум |
функции |
называют |
||||||||||||||||||||
экстремумами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Определение 10.3. Точка, в которой обе частные производные равны |
|||||||||||||||||||||||||||||
нулю, |
т.е. |
|
|
|
|
¶z |
= 0, |
|
|
¶z |
= 0, |
называется стационарной |
точкой |
функции |
||||||||||||||||
|
|
|
|
|
|
|
¶y |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
z = f ( x; y) . |
место теорема |
10.1. (необходимый признак существования |
||||||||||||||||||||||||||||
|
Имеет |
|||||||||||||||||||||||||||||
экстремума). Если P0 (x0 ; y0 ) |
точка |
экстремума дифференцируемой функции |
||||||||||||||||||||||||||||
z = f (x; y) , то z¢x (x0 ; y0 ) = 0, z¢y (x0 ; y0 ) = 0 . |
|
|
|
|
|
|
|
|||||||||||||||||||||||
19

Этот признак не является достаточным условием. Сформулируем достаточный признак.
Теорема 10.2. Пусть в стационарной |
точке P0 (x0 ; y0 ) |
и некоторой ее |
|||||||||||||
окрестности |
функция |
имеет непрерывные |
частные |
производные |
до |
второго |
|||||||||
¢¢ |
(x0 |
¢¢ |
|
¢¢ |
|
|
|
|
|
|
|
|
|
||
порядка zxx |
; y0 ), zxy (x0 ; y0 ), |
zyy (x0 ; y0 ) . |
|
|
|
|
|
|
|||||||
Составим определитель |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
¢¢ |
(x0 ; y0 ) |
¢¢ |
(x0 |
; y0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
D = |
zxx |
zxy |
. |
|
|
|
|
|
|
||||
|
|
|
¢¢ |
(x0 ; y0 ) |
¢¢ |
(x0; y0 ) |
|
|
|
|
|
|
|||
|
|
|
zxy |
zyy |
|
|
|
|
|
|
|
||||
Тогда: |
1) если |
D > 0 , |
то |
функция z = f (x; y) |
имеет в точке |
P0 (x0 ; y0 ) |
|||||||||
экстремум. |
Причем |
|
максимум, |
¢¢ |
|
|
и |
минимум, если |
|||||||
|
если zxx (x0 ; y0 ) < 0 |
||||||||||||||
¢¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zxx (x0 ; y0 ) > 0 ; |
D < 0 , |
|
|
|
|
z = f (x; y) |
|
точке P0 (x0 ; y0 ) |
|
|
|||||
2) если |
то функция |
в |
не |
имеет |
|||||||||||
экстремума; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) в случае, если D = 0 , вопрос об экстремуме в точке P0 (x0 ; y0 ) |
остается |
||||||||||||||
открытым. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схема исследования функции z(x; y) на экстремум
1. Находим стационарные точки.
1.1. Находим частные производные z¢x и z¢y функции z=f(x; y).
ìz¢ = 0,
1.2. Находим решения системы уравнений í x
îz¢y = 0.
2. Проверяем выполнение достаточного условия экстремума в каждой
стационарной точке. |
|
|
¢¢ |
|
|
¢¢ |
¢¢ |
, |
z |
, |
z |
||
2.1. Находим частные производные второго порядкаz |
yy |
xy |
||||
xx |
|
|
|
|
функции z=f(x; y).
2.2. Определяем значения частных производных второго порядкаz¢¢ ,
xx
z¢yy¢ , z¢xy¢ в стационарной точке.
2.3. Вычисляем значение определителя вида
D= z¢xx¢ (x0 ; y0 ) z¢xy¢ (x0 ; y0 )
z¢xy¢ (x0 ; y0 )
в каждой из стационарных точек и,
z¢yy¢ (x0 ; y0 )
используя достаточное условие, делаем вывод относительно наличия экстремума в каждой из них.
Пример 10.1. Исследовать на экстремум функцию z(x; y) = xy(1 - x - y) .
Решение.
1. Находим стационарные точки.
1.1. Найдем частные производные z¢x и z¢y функции z=f(x; y).
z¢x = ¶ (xy(1 - x - y)=) y(1 - x - y) + xy(-1) = y - 2xy - y2.
¶x
20
z¢y |
= |
¶ |
(xy(1 - x - y)=) |
x(1 - x - y) + xy(-1) = x - x2 - 2xy. |
|
|
|
||||||||||
|
|
|
|
||||||||||||||
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2. Для нахождения стационарных точек решим систему уравнений |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
ìzx¢ = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
í |
¢y = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îz |
|
|
|
|
|
|
|
|
ì |
- 2xy - y |
2 |
= 0; |
ìy(1- 2x - y) = 0; |
|
|
|
|
|
|
|||||||
ïy |
|
|
|
|
|
|
|
||||||||||
í |
- x2 - 2xy = 0. |
Þ í |
|
|
|
|
|
|
|
|
|
|
|||||
ïx |
îx(1 - x - 2 y) = 0. |
|
|
|
|
|
|
||||||||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эта система распадается на совокупность систем |
|
|
|
|
|
||||||||||||
ìx = 0; |
2) |
ìx= 1; |
3) |
ìx= 0; |
ì1 - 2x - y 0; =ìx 1/ 3; |
|
|
|
|||||||||
1) í |
|
|
í |
|
í |
4) |
í |
- 2 y 0. |
Þ |
í |
|
|
|
||||
îy = 0. |
|
|
îy= 0. |
|
îy= |
1. |
î1 - x |
= |
îy 1/ 3.= |
|
|
||||||
В итоге получаем такой набор стационарных точек: M1 (0; 0), |
M 2 (1; 0), |
|
|
||||||||||||||
M 3 (0; 1) и M 4 (1/3; 1/3). |
|
|
|
|
|
|
|
|
|
|
|||||||
2. Проверим выполнение |
достаточного условия экстремума для каждой |
||||||||||||||||
из них. |
|
|
|
|
|
|
|
|
|
|
|
|
порядкаz¢¢ , |
z¢¢ |
|
z¢¢ |
|
2.1. Найдем |
|
частные |
|
производные |
второго |
, |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xx |
yy |
|
xy |
исследуемой функции z=f(x; y).
¢¢ |
|
|
|
¶ |
|
|
|
¢ |
|
|
|
|
¶ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
)= ¶x (y - 2xy - y )= -2 y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
zxx |
= ¶x (zx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
¢¢ |
|
= |
¶ |
|
¢ |
=) |
|
¶ |
(x |
- x |
2 |
- 2xy)= -2x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
¶y |
|
|
¶y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
zyy |
|
(zy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
=) |
¶ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢¢ |
|
|
¢¢ |
|
|
|
|
|
|
¢ |
|
|
(x - x - 2xy)=1 - 2x - 2 y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
¶x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
zxy |
= zyx |
= ¶x (zy |
|
|
z¢¢ |
|
|
|
|
|
z¢¢ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2.2. Определим значения частных производных z¢¢ , |
|
|
, |
|
|
|
исследуемой |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xx |
|
|
yy |
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
||||
функции z=f(x; y) в стационарных точках (0; 0), (1; 0), (0; 1) и (1/3; 1/3). |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
z¢¢ |
(0;0) = 0; |
z¢¢ |
(1;0) = 0; |
z¢¢ |
(0;1) = -2; |
z¢¢ |
æ 1 |
; |
1 ö |
|
|
2 |
; |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
÷ = - |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
xx |
|
|
|
|
|
|
|
|
|
xx |
|
xx |
|
xx |
è 3 3 ø |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
z¢¢ |
(0;0) = 0; |
z¢¢ |
(1;0) = -2; |
z |
¢¢ (0;1) = 0; |
z¢¢ |
æ |
1 |
; |
1 ö |
= - |
2 |
|
; |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
yy |
|
|
|
|
|
|
|
|
|
|
yy |
|
|
yy |
yy |
è |
3 3 ø |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
z¢¢ |
(0;0) =1; |
|
z |
¢¢ |
(1;0) = -1; |
z¢¢ (0;1) = -1; |
z¢¢ |
æ |
1 |
; |
1 ö |
|
= - |
1 |
|
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
÷ |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
xy |
|
|
xy |
xy è |
|
|
|
3 ø |
|
|
|
|
|||||||||||||||
2.3. Вычислим определитель D в каждой из этих точек. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
D(0;0)= = |
|
0 |
1 |
|
|
|
0 -1= -1 < 0 , |
|
следовательно, |
в стационарной |
|
|
|
|
точкеM1 (0; 0) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
экстремума нет.
21
D(1;=0)= |
|
|
0 |
|
-1 |
|
|
|
0 -1= -1 < 0 , следовательно, в |
стационарной |
точке M 2 (1; 0) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
-1 |
-2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
экстремума нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
D(0;1)= = |
|
-2 |
|
|
-1 |
|
|
|
0 -1= -1 < 0 , следовательно, в стационарной точке M 3 (0; 1) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
экстремума нет. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
æ |
1 |
|
|
1 |
|
|
|
|
2 |
- |
|
1 |
|
4 |
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
ö |
|
|
|
|
|
|
3 |
|
|
|
|
следовательно, в стационарной точке |
|
|||||||||||||||||||||||||
Dç |
=; |
|
|
|
|
÷= |
|
|
1 |
|
|
|
2 |
|
|
|
- |
|
= |
|
> 0, |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
è |
3 3 |
|
|
ø |
- |
- |
|
9 9 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
æ 1 |
|
1 |
|
2 |
|
|
1 |
|
1 |
|
||||
|
æ |
1 |
|
|
1 ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ö |
|
æ |
|
ö |
|||||||||||||
M 4 ç |
|
|
|
; |
|
|
|
÷ экстремум есть. Так как |
z¢¢xx ç |
|
; |
|
÷ = - |
|
< 0 , то точка |
M 4 ç |
|
; |
|
÷ – |
||||||||||||||||||||
|
|
|
|
|
|
|
3 |
3 |
|
|
||||||||||||||||||||||||||||||
|
è |
3 3 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è 3 |
|
ø |
|
è |
3 3 |
ø |
|||||||||||||||
точка максимума.
æ |
1 |
|
1 ö |
|
1 |
|
1 |
æ |
|
1 |
|
1 ö |
|
1 |
|
|||
Значение функции в точке максимума zmax ç |
|
; |
|
÷ |
= |
|
× |
|
ç1 |
- |
|
- |
|
÷ |
= |
|
. |
|
3 |
3 |
3 |
3 |
3 |
3 |
27 |
||||||||||||
è |
|
ø |
|
|
è |
|
|
ø |
|
|
||||||||
График исследуемой функции z(x; y) = xy(1 - x - y) представлен на рис. 10.1.
Рис. 10.1
Пример 10.2. Исследовать на экстремум функцию z = 3x + 6 y + x2 - xy + y2 .
Решение |
|
|
|
|
1. Находим стационарные точки. |
и z¢ функции z = f (x, y) . |
|||
1.1. Найдем частные производные z¢ |
||||
|
|
|
x |
y |
z¢x = |
¶ |
|
(3x + 6 y + x2 - xy + y2 )= 3 |
+ 2x - y. |
|
|
|||
¶x |
||||
z¢y = |
¶ |
|
(3x + 6 y + x2 - xy + y2 )= 6 |
- x + 2 y. |
¶y |
|
|||
22
ìz¢x = 0,
Для определения стационарных точек решим систему уравнений í
îz¢y = 0.
ì3 + 2x - y =0, |
ì6 + 4x - 2 y = 0, |
|
ì12 + 3x = 0, = ìx -4, |
||||||
í |
- x + 2 y = 0. |
Þ í |
- x |
+ 2 y = 0. |
Þ í |
Þ í |
-5. |
||
î6 |
î6 |
= |
îy 3 |
+ 2x.= |
îy |
||||
Стационарная точка имеет координаты (–4; –5). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2. Проверим выполнение достаточного условия экстремума. |
|
|
||||||||||||||||||||||||||||
2.1. Найдем частные производные второго порядка z¢¢ , |
z¢¢ , z¢¢ |
функции |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xx |
|
yy |
xy |
|
||
z=f(x; y). |
|
|
|
|
¶ |
|
|
|
|
|
|
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¢¢ |
|
|
(z |
¢ |
)= |
(3 + 2x - y)= 2. |
|
|
¶ |
|
|
¶ |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
z |
= |
¶x |
¶x |
¢¢ |
= |
¶y |
¢ |
= |
¶y (6 |
- |
x |
+ |
2 y) |
= |
2. |
|||||||||||||||
|
xx |
|
|
|
|
x |
¶ |
|
¶ |
|
|
zyy |
|
(zy |
) |
|
|
|
||||||||||||
|
¢¢ |
|
¢¢ |
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
= |
|
|
)= ¶x (6 - x + 2 y)= -1. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
zxy |
= z yx |
¶x (z y |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2.2. Частные |
|
|
|
¢¢ |
¢¢ |
|
¢¢ |
имеют |
постоянные |
|
значения в |
|||||||||||||||||||
производные zxx |
, zyy , |
zxy |
|
|||||||||||||||||||||||||||
любой точке плоскости Оху. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
2.3. Вычислим значение определителя D в точке (-4;-5). |
|
|
|
|
|
|||||||||||||||||||||||||
D(-4;-5)= |
|
2 |
-1 |
|
|
|
4 -1 =3 >0, следовательно, |
в |
стационарной точке(–4; –5) |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
= |
2 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(- 4;-5) – точка |
|||||||
экстремум |
есть |
|
|
,и так |
¢¢ |
|
|
> 0 , |
то |
точка |
||||||||||||||||||||
|
|
как zxx (- 4;-5) = 2 |
||||||||||||||||||||||||||||
минимума. Найдем минимальное значение функции z(-4;-5)= |
|
-21. |
|
|
||||||||||||||||||||||||||
График исследуемой функции |
z(x, y) = 3x + 6 y + x2 - xy + y2 |
|
|
|||||||||||||||||||||||||||
представлен на рис. 10.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Рис. 10.2
23

11. Наибольшее и наименьшее значение функции
Пусть функция z = f (x; y) определена и непрерывна в ограниченной замкнутой области D , тогда она достигает в этой области своего наибольшего
и наименьшего значений.
Порядок действий при нахождении наибольшего и наименьшего значений
дифференцируемой |
|
в |
|
замкнутой |
областиD |
функции z = f (x; y) состоит в |
||||||||||||||||||||||
следующем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции, принадлежащие D , |
|
|
|
||||||||||
|
1. |
|
|
Найдем |
|
|
|
все |
|
стационарные |
точки |
|
|
и |
||||||||||||||
вычислим значения функции в них. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2. |
Найдем наибольшее и наименьшее значения функцииz = f (x; y) |
|
на |
||||||||||||||||||||||||
границе области и ее значения в угловых точках области. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
3. |
|
|
Сравним |
|
|
все |
найденные значения функции и выберем из них |
||||||||||||||||||||
наибольшее и наименьшее. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
Пример. |
|
Найдите |
|
наибольшее |
и |
наименьшее |
|
|
значения |
|||||||||||||
функции |
|
|
z(x; y) = x2 + y2 - xy + x + y |
в замкнутой области, |
заданной системой |
|||||||||||||||||||||||
|
|
|
|
|
|
ìx £ 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
неравенств |
ï |
|
£ 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
íy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
î2x + 3y + 6 ³ 0. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Решение. 1. Найдем стационарные точки из системы уравнений |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
ì ¢ |
= |
¶ |
|
(x |
2 |
+ y |
2 |
- xy + x + y ) = 2x - y +1 =0; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ïzx |
|
¶x |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
í |
|
¶ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ï |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ïz¢y |
= ¶y (x |
|
+ y |
|
- xy + x + y ) = 2 y - x +1 =0. |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система |
имеет |
единственное |
решение(-1;-1). |
Стационарная точка |
|||||||||||||||||||||||
М(-1;-1) |
лежит |
внутри |
области(область |
D изображена |
на рис.11.1). Найдем |
|||||||||||||||||||||||
значение функции в ней: |
z1 = f (-1; -1)= |
-1. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Исследуем поведение функции на границе области. Для этого разобьем |
||||||||||||||||||||||||||||
границу |
|
|
|
на |
|
|
|
три |
|
отрезкаАО, |
ОВ, АВ. На |
отрезке АО |
имеем: |
|||||||||||||||
y = 0, - 3 £ x £ 0, z= |
|
x2 + x . |
Найдем |
значения |
функции |
на |
концах |
отрезка |
||||||||||||||||||||
[-3;0] в |
|
|
точках A(-3;0) |
и O(0;0) . Получим z2 |
= f (-3;0) |
6,=z3 |
f (0;=0) |
0 . |
||||||||||||||||||||
Теперь |
|
попробуем найти стационарную точку на этом отрезке. Для этого |
||||||||||||||||||||||||||
найдем |
производную zx¢ = 2x +1 |
и |
приравняем |
ее к |
нулю, получим |
x = - |
1 |
. |
||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
æ |
|
1 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Точка |
ç - |
|
|
; 0 ÷ лежит внутри отрезка AO . Значение функции в этой точке будет |
||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
z4 = f |
æ |
|
1 |
ö |
|
1 |
. Перейдем к отрезку OB . |
|
|
|
|
|
|
|
|
|
||||||||||||
ç- |
= |
;0 ÷ |
- |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
è |
|
2 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
24

|
|
|
|
|
|
|
|
|
|
|
|
Рис.11.1 |
|
|
|
Здесь |
x = 0, - 2 £ y £ 0, =z |
y2 + y . Вычислим значение функции в точке |
|||||||||||||
B(0;-2) . Получим |
z5 = f (0;-2) = 2 . При |
y = 0 |
значение функции |
вычислено |
|||||||||||
ранее. |
|
|
|
|
|
|
|
|
|
|
|
|
|
функцииz = y2 + y , |
|
Попробуем |
найти |
|
стационарную |
точку |
лежащую |
||||||||||
внутри отрезка OB . Для |
этого |
найдем z¢y = 2 y +1 и приравняем |
ее к нулю, |
||||||||||||
|
|
1 |
|
|
|
|
æ |
|
|
1 |
ö |
|
|
|
|
получим y = - |
|
|
. Точка ç |
0; |
- |
|
÷ лежит внутри отрезка OB . Значение функции в |
||||||||
2 |
|
2 |
|||||||||||||
|
|
|
|
|
|
è |
|
|
ø |
|
|
|
|
||
æ |
|
1 |
ö |
|
1 |
|
|
|
|
|
|
|
|
|
|
ней z6 = f ç |
0;- =÷ |
- |
|
. |
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
|
|
|
|
|
|||||||
è |
|
2 ø |
|
|
|
|
|
|
|
|
|
|
|||
|
Рассмотрим поведение функции z |
на отрезке AB . Значение функции на |
|
||||||||||||||||||||||||||
концах |
|
отрезка (в точках А |
и В) |
вычислены |
ранее. |
Найдем стационарную |
|
||||||||||||||||||||||
точку, |
лежащую |
|
внутри |
этого |
|
отрезка. Для этого из |
уравнения |
прямой AB |
|
||||||||||||||||||||
2x + 3y + 6 = 0 |
выразим у: |
y = - |
2 |
x - 2 . |
Подставим |
найденное |
у |
в функцию |
|
||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
19 |
|
|
|
|
|
|
|
|
|
|
||
z = x2 + y2 - xy + x + y . |
Получим |
|
|
|
z = |
x2 + 5x + 2 |
и |
найдем |
|
стационарную |
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
38 |
|
|
|
|
точку |
|
этой |
функции |
при |
условии, что |
-3 £ x £ 0 . |
Имеем: z¢x |
= |
x + 5 = 0 , |
|
|||||||||||||||||||
9 |
|
||||||||||||||||||||||||||||
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x = - |
. |
Таким |
|
образом, |
стационарная |
точка |
лежащая внутри |
отрезка |
,АВ |
|
|||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
38 |
|
|
|
|
|
|
|
|
æ |
45 |
|
|
|
46 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
; - |
|
|
|
|
|
|
|
|
|
|
|
|||||||
имеет |
|
|
|
|
координаты |
ç- |
|
|
|
÷ . |
|
Значение |
|
функции |
в |
н |
|||||||||||||
|
|
|
|
38 |
38 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|||
æ |
|
|
45 |
|
46 |
ö |
|
73 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z7 = f ç |
- |
|
;- |
= |
÷ |
- |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
38 |
76 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
è |
|
|
|
38 |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
25
Сравнивая все найденные значения функции z1, z2 ,...z7 , делаем вывод, что
в заданной области функцияz принимает наименьшее |
значение(-1) в точке |
M (-1; -1) . Наибольшее значение, равное 6, функция |
принимает в точке |
A(-3;0) . |
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1.Егоров В.Я., Недвецкая А.И., Толмачева М.А. Сборник домашних заданий по курсу высшей математики: метод. руководство для студентов всех специальностей дневной формы обучения. – Екатеринбург : УрГУПС, 2004. – 56 с.
2.Письменный Д.Т. Конспект лекций по высшей математике. – М. : Айрис-
пресс, 2003. – Ч. 1. – 288 с.
3.Рябушко А.П. Сборник индивидуальных заданий по высшей математике.
Ч. 1. – Минск : Высш. шк., 1990. – 270 с.
4.Фихтенгольц Г.М. Основы математического анализа. : учеб. для вузов. –
СПб. : Лань, 2001. – Т.1. – 464 с.
5. Лунгу К. Н., Письменный Д. Т., Федин С. Н. и др. Сборник задач по высшей математике: 1 курс. − М. : Айрис-пресс, 2004.
26

Типовой расчет «Функции нескольких переменных»
Вариант № 1
1. Найдите область определения функций:
a) z = 
 9 - x2 - y2 +
9 - x2 - y2 + 
 x2 + y2 - 4 ; б) z =
x2 + y2 - 4 ; б) z = 
 3 + x - y ×ln(x +1) . 2. Найдите частные производные первого порядка функции
3 + x - y ×ln(x +1) . 2. Найдите частные производные первого порядка функции
z= ln(x3 + 2 y2 ) + cos xy .
3.Найдите частные производные функцииz = z( x; y) , заданной неявно
уравнением x2 + y2 + z2 + 2xz - 4 yz =1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4. |
Найдите |
|
градиент |
функцииz = x 2 |
- 2xy - 2 y 2 |
в |
точке |
|
|
М0(1;2) |
и |
||||||||||||
производную по направлению вектора M 0 M1 , где M1(2;4) . |
|
|
|
|
|
|
|
|
|||||||||||||||
5. |
Составьте |
уравнения |
касательной плоскости и |
нормали |
|
к поверхности |
|||||||||||||||||
x2 + y2 + z2 + 6z - 4x +8 = 0 в точке M 0 (2;1; -1) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
6. |
Исследуйте на экстремум функцию z = x3 - 3x2 - 2 y2 +10 y - 4 . |
|
|
|
|||||||||||||||||||
7. |
Найдите наибольшее и наименьшее значение |
функцииz = f (x; y) |
в |
||||||||||||||||||||
замкнутой области D, ограниченной заданными линиями |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
z = 6x2 + 6xy + 2 y2 + 2 y + 6x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x = 0;= y =0; y x + 3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Вариант № 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Найдите область определения функций: |
а) z = ln(1 - y - |
1 |
|
x2 ) + |
|
|
|
; |
|
|
|
|
||||||||||
|
xy |
|
|
|
|||||||||||||||||||
4 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) z = arcsin( x - y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Найдите частные производные первого порядка функции z = |
1 |
|
|
. |
|
|||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||
arctg xy |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
Доказать, |
что |
|
|
функция z = z( x; y) , |
заданная |
|
неявно |
|
|
уравнением |
||||||||||||
4sin(3x + 2 y + 5z)= 3x + 2 y + 5z , удовлетворяет уравнению |
¶z |
+ |
¶z |
+1 = 0 . |
|
||||||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶x |
¶y |
|
|
|
|||||
4. |
Найдите |
градиент |
z = x 2 + xy + y 2 + 3 |
в |
|
точке |
|
М0(1;2) |
и |
||||||||||||||
функции |
|
|
|
||||||||||||||||||||
производную по направлению вектора M 0 M1 , где М1(1;1). |
|
|
|
|
|
|
|
|
|||||||||||||||
5. |
Составьте уравнения касательной плоскости и нормали к поверхности |
|
|||||||||||||||||||||
|
z = |
x 2 |
|
+ |
y 2 |
|
в точке М0(2;3;2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6. |
Исследуйте на экстремум функцию z = x2 - 4x - 4 y3 +12 y2 - 5 . |
|
|
|
|||||||||||||||||||
7. |
Найдите наибольшее и наименьшее значение |
функцииz = f (x; y) |
в |
||||||||||||||||||||
замкнутой области D, ограниченной заданными линиями |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
z = x2 + 2 y2 - 4 y + 8x +1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x = -5; x =0; y = 0; y = 2 .
27
