
- •Высшая математика
- •Содержание
- •Глава I. Элементы линейной алгебры
- •§1.1. Матрицы и определители
- •§1.2. Системы m линейных алгебраических уравнений с m неизвестными
- •1.3. Операции над матрицами
- •1.4. Обратная матрица. Матричные уравнения и системы линейных уравнений
- •Решение систем линейных уравнений с помощью обратной матрицы
- •1.5. Собственные числа и собственные векторы матрицы
- •Глава 2. Векторная алгебра
- •§2.1 Векторы. Линейные операции над векторами
- •§2.2. Скалярное произведение
- •Свойства скалярного произведения
- •§2.3. Векторное произведение векторов
- •Свойства векторного произведения
- •§2.4. Смешанное произведение трех векторов
- •Глава III. Аналитическая геометрия
- •§ 3.1. Прямая линия на плоскости
- •Угол между двумя прямыми
- •Расстояние от точки до прямой
- •§ 3.2. Кривые второго порядка на плоскости
- •§ 3.3. Общее уравнение кривых второго порядка Преобразование уравнения кривой второго порядка к каноническому виду
- •§ 3.4. Плоскость в пространстве
- •§ 3.5. Прямая в пространстве. Прямая и плоскость
- •Глава IV. Математический анализ
- •§4.1. Основные элементарные функции, некоторые свойства и графики
- •§4.2. Предел функции. Замечательные пределы. Непрерывность функции
- •Замечательные пределы
- •Непрерывность функции
- •Разрывы функции
- •§4.3. Дифференцирование функций. Основные формулы дифференцирования
- •Основные правила дифференцирования
- •§4.4. Уравнения касательной и нормали к плоской кривой
- •§4.5. Производные высших порядков. Правила Лопиталя
- •Правила Лопиталя
- •§4.6. Монотонность функций. Экстремумы. Наибольшее и наименьшее значения функции на отрезке
- •§4.7. Промежутки выпуклости, вогнутости графика функции. Точки перегиба. Асимптоты
- •§4.8. Параметрически заданные функции. Векторная функция скалярного аргумента. Кривизна плоской кривой
- •Список рекомендуемой литературы
Глава I. Элементы линейной алгебры
§1.1. Матрицы и определители
Матрицей называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Матрица записывается в виде:

или сокращенно как А=(aij), где i=1,2,…,m; i=1,2,…,n.
Матрица, содержащая один столбец или одну строку, называется вектором или вектором-столбцом, вектором-строкой соответственно.
Матрица, у которой число строк равно числу столбцов и равно n, называется квадратной матрицей n-го порядка.
Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали (т.е. с индексами ij) равны нулю.
Единичной называется диагональная матрица с единицами на главной диагонали (обозначается Е).
Нулевой называется матрица, все элементы которой равны нулю.
Примеры матриц: а) квадратная; б) диагональная; в) единичная; г) нулевая:
а)
 ;
б)
;
б)![]() ;
в)
;
в)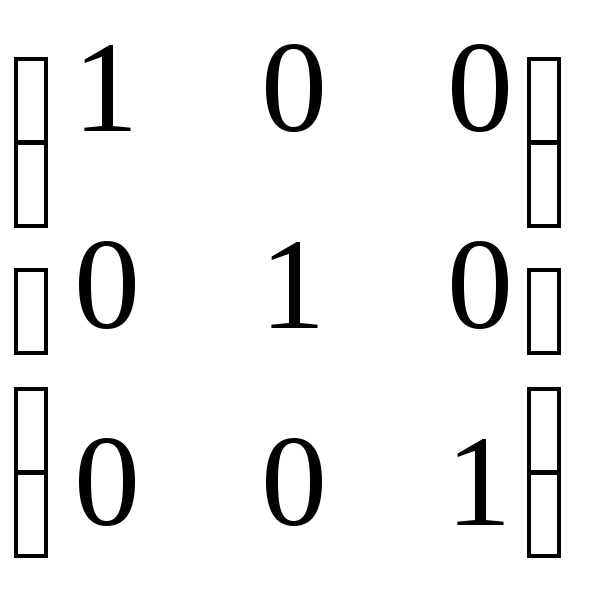 ;
г)
;
г)![]() .
.
Каждой квадратной матрицей n-го порядка можно поставить в соответствие число Δ(detA), называемое ее определителем.
При n=1 А=(а1); Δ=detA=а1.
При
n=2
 ;
Δ=a11a22-a12a22.
;
Δ=a11a22-a12a22.
При
n=3
 ;
;
Δ= =a11a22a33+a12a23a31+a21a32a13-a13a22a31-a21a12a33-
=a11a22a33+a12a23a31+a21a32a13-a13a22a31-a21a12a33-
-a32a23a11.
Для вычисления определителей второго и третьего порядков можно пользоваться следующими схемами:
![]() при
n=2;
при
n=2;
 при
n=3.
при
n=3.
Основные свойства определителей:
Значение определителя не изменяется, если заменить его строки столбцами и наоборот.
При перестановке двух параллельных рядов определитель меняет знак.
Определитель, имеющий два одинаковых ряда, равен нулю.
Общий множитель элементов какого-либо ряда можно вынести за знак определителя в качестве сомножителя.
Определитель не изменится, если к элементам одного ряда прибавить элементы параллельного ряда, умноженные на одно и то же число.
Минором некоторого элемента aij определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых стоит элемент аij. Обозначается минор как Мij.
Алгебраическим дополнением элемента aij называется минор Мij, умноженный на (-1)i+j, т.е. Аij =(-1)i+jMij.
Определитель любого порядка можно представить как сумму произведений элементов какого-либо ряда определителя на соответствующие им алгебраические дополнения.
_________________
1.1.1. Вычислить определители:
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() .
.
Ответ: а) 26; б) 7; в) 1.
При каких значениях а обращается в ноль определитель Δ=
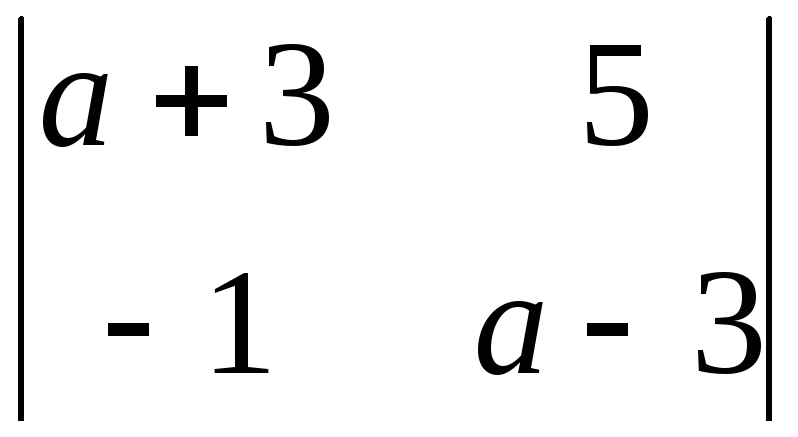 ?
?
Ответ: ±2
Вычислить определитель по правилу треугольников
а)
 .
.
Ответ: а) 47; б)0 .
При каких значениях а обращается в ноль определитель
 ?
?
Ответ: (1;-2)
Вычислить определитель путем разложения по элементам 3-го столбца
![]()
 .
.
Ответ: (-48).
Вычислить определитель с помощью разложения по элементам второй строки
 .
.
Ответ: (-15).
Вычислить определители
а)

Ответ: а) 0, б) 28.
Вычислить определители
![]()
Ответ: а) -38; б) 27; в) -1; г) 2а; д) sin2-sin2.
Вычислить определитель с помощью разложения по элементам какого-либо ряда и проверить по правилу треугольников
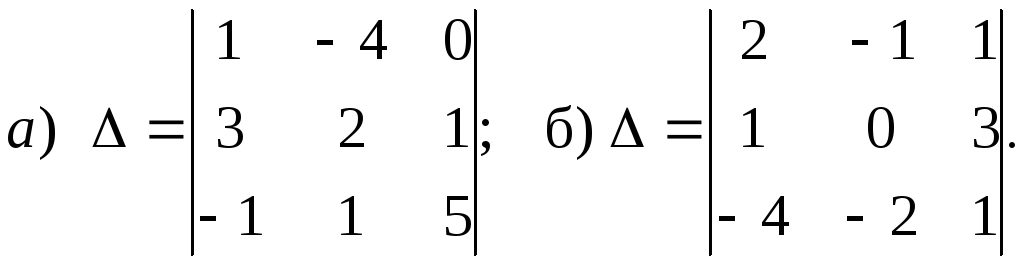
Ответ: а) 73; б) 23.
Упростить и вычислить определители:

Ответ: а) -156; б) 0.
Решить уравнение
 .
.
Ответ: (2;3).
