Математическое описание сау и ее элементов

Для анализа и синтеза САУ необходимо иметь математическое описание систем. Для этой цели системы разделяются на отдельные элементы (звенья, подсистемы) и составляются уравнения, описывающие поведение этих элементов. Уравнения составляются на основании анализа физических, химических, технологических, экономических, социальных и иных процессов, происходящих в конкретных элементах. Используются соответствующие законы (закон сохранения массы, энергии, вещества и пр.), применяются специальные исследования и экспериментальные методы для получения математического описания звеньев систем.

Все математические модели (ММ) разделяются на:

1. ММ стационарных и нестационарных САУ;

2. ММ САУ с распределенными и сосредоточенными параметрами;

3. Статические характеристики;

4. Динамические ММ в виде

1. Дифференциальные уравнения;

2. Разностные уравнения (для дискретных САУ);

3. Передаточные функции (ММ в виде структурной схемы);

4. Временные и частотные характеристики.

Линеаризация статических характеристик

Статическая характеристика - связывает входную величину с выходной звена, когда все остальные величины постоянны (при установившихся внутренних процессах): Y=F(X);

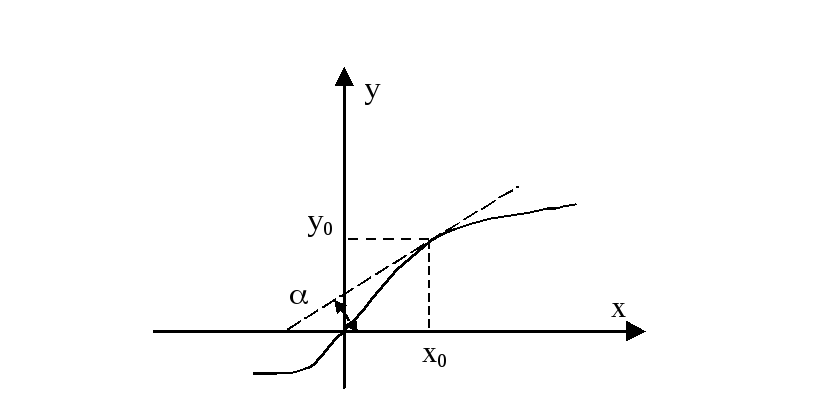
Линеаризация проводится, если в окрестности некоторой рабочей точки (х₀,y₀)линеаризованная функция непрерывна:

если члены старших порядков отбросить, то получаем:

или

Отсюда: ;;;;.

Линеаризация проводится с погрешностью! обязательно в окрестности некоторой (рабочей) точки.

Динамические характеристики звена

Позволяют описать поведение звена (системы) во времени. Разделяются на дифференциальные и разностные уравнения. Для случая многомерного звена данные уравнения связывают входные и выходные переменные и их производные (сколь угодно большого порядка). Данные математические модели могут быть как в виде одного уравнения, так и в виде систем уравнений. В одномерном случае имеет место связь между одной входной и одной выходной переменными и их производными:

.

Применяя формулу Тейлора и отбрасывая старшие производные (2-й степени и выше) получаем:

,

или линейное уравнение с постоянными коэффициентами, с учетом того, что

:

.

Такое уравнение описывает поведение звена только в окрестности некоторой точки .

При значительном удалении от точки линеаризации данное уравнение как правило несправедливо. Полученное уравнение также называется уравнением в отклонениях или уравнением вариации. Практически изаменяют наxиy. Тогда окончательно имеем дифференциальное уравнение:

,

или в операторной форме .

Откуда получается : .

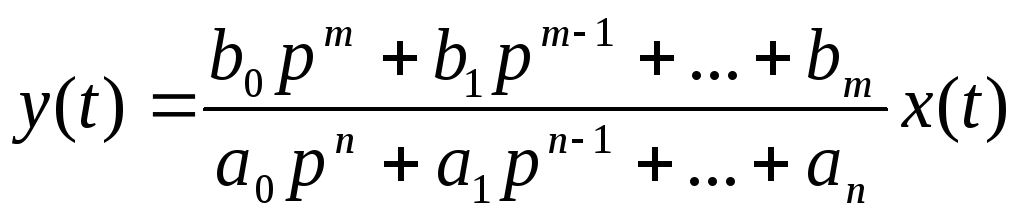Можно обозначить Q(p) =- собственный полином,

R(p) =- входной полином.

При наличии возмущений уравнение, описывающее звено, усложняется:

,

а в операторной форме:

, или

, где- полином возмущения.

Полученные уравнения носят названия уравнения вход-выход.

Уравнения исследуются методами:

1. аналитическим,

2. численным,

3. операторным,

4. частотным.

Аналитические и численные методы решения дифференциальных уравнений исследуются в соответствующих разделах математического анализа и вычислительной математики.

Операторный методбазируется на использовании оператора Лапласа (или Карлсона). Преобразование Лапласа-Карлсона основано на применении понятийоригинала и изображения .

Оригинал - функция вещественного аргумента.

Изображение - функция комплексного аргумента.

Для того, чтобы функция была оригиналом, она должны удовлетворять условиям Дирихле:

1. Функция f(t) растет ограниченно в рассматриваемом промежутке:

.

2. На рассматриваемом промежутке времени функция ограничена сверху и снизу (имеет maxиmin).

3. На рассматриваемом промежутке функция имеет конечное число разрывов первого рода. Разрывы второго рода отсутствуют.

При соблюдении всех этих условий функция является оригиналом.

Для получения изображения используется прямое преобразование Лапласа: .

С помощью данного преобразования переходят к изображению:

;=ℒ;

;=ℒ;

Обратное преобразование по Лапласу: .