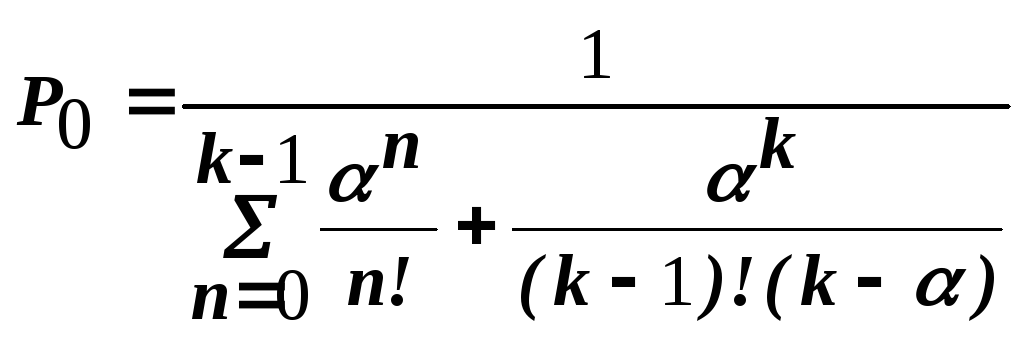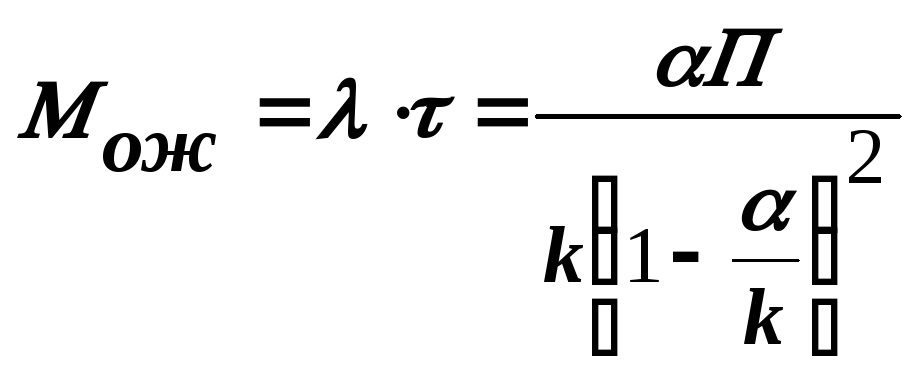Обслуживание требований

По периоду занятия свободных приборов:

1. подключение в строгом порядке,

2. в порядке освобождения,

3. в случайном порядке.

На практике имеется достаточно сложные, в том числе и комбинированные системы обслуживания.

Время обслуживания

Время обслуживания – важнейшая характеристика канала, определяет его пропускную способность, в большинстве систем является случайной величиной.

Основные причины:

1. нестабильность работы канала, в том числе с участием человека;

2. неидентичность поступающих в систему требований.

Функция распределения вероятностей того, что время обслуживания меньше некоторого заданного

Используют показательный знак распределения:

(3)

Плотность распределения:

(4)

Интенсивность обслуживания:

(5)

СМО с показательным законом распределения времени обслуживания обладает важным свойством – если некоторое требование может быть обслужено несколькими приборами одновременно, то интенсивность обслуживания равна сумме интенсивностей этих приборов. Для однотипных приборов среднее время обслуживания уменьшается в раз.

Контрольные вопросы.

1. Какова общая постановка задачи массового обслуживания?

2. Какие системы обслуживания называются СМО с ожиданием? с отказами? с потерями?

3. Каковы основные элементы СМО?

4. Что называется простейшим потоком требований?

5. Что называется интенсивностью обслуживания?

Лекция 8. Системы массового обслуживания с ожиданием

1. Общее описание СМО с ожиданием

2. Состояние системы и их вероятности

3. Простейшие частные случаи (одноканальная и двухканальная системы)

Есть некоторый поток требований, который поступает в систему. Поток характеризуется показателем – интенсивность потока. Система имеет- каналов. Показатель интенсивности обслуживания:– среднее число заявок обслуживаемых одним каналом в единицу времени.

Введем новый показатель: напряженность обслуживания:

(1)

Если все каналы заняты, возникает очередь.

Условие работоспособности системы:

(2)

При невыполнении условия (2) , очередь на обслуживание может возрастать неограниченно.

Работу системы будем описывать её состояниями, различающимися количеством требований , имеющихся в системе.

Все состояния будем характеризовать их вероятностями

Обязательное условие:

Наиболее важной является – вероятность того, что в системе отсутствуют требования.

(3)

Рассмотрим частные случаи, общей формулы (3):

причем ;

Вероятность того, что в системе находится требований, равна:

(нет очереди)

(4)

Рассмотрим частные случаи:

Качество обслуживания характеризуется средним временим ожидания начала обслуживания и средней длиной очереди. Обозначим через среднее время ожидания.

(5)

Частные случаи:

;

Вероятность того, что все каналы заняты:

(6)

Частные случаи:

;

Средняя длина очереди (математическое ожидание длины очереди):

(7)

Частные случаи:

; .

Характеристикой системы является также среднее время пребывания в системе. Это сумма среднего времени обслуживания и среднего времени ожидания в очереди.

Дополнительной характеристикой качества работы системы является среднее число занятых каналов, как степень загрузки системы.

.

(8)

Пример.

В порту имеется 2 причала для разгрузки судов, интенсивность потока судов приходящих в порт равно 0,8 (судна/сутки). Среднее время разгрузки 1 судна – двое суток. Найти среднюю длину очереди и среднее время пребывания судна в порту.

Решение:

(двухканальная система), показатель интенсивности входящего потока.суток,.

Рассчитаем показатель напряженности.

- система работоспособна

В среднем 11,1% всего времени причалы свободны.

В среднем 17,8% времени занят один причал, а второй при этом свободен.

В среднем 14,1% всего времени причалы заняты, система нагружена, но еще не перегружена.

Найдем вероятность того, что все причалы заняты.

или

Среднее время ожидания начала разгрузки:

(суток)

Среднее время пребывания в порту:

(суток)

Средняя длина очереди:

(судна)

Среднее число занятых причалов:

.

Контрольные вопросы

1. Как описывается в общем виде работа СМО с ожиданием?

2. Какими параметрами задается СМО с ожиданием?

3. Что представляют собой состояния системы?

4. Каковы характеристики качества обслуживания для СМО с ожидания?