Лекция 12. Многопродуктовые модели управления запасами

1. Общая постановка задачи уравнения запасами для многопродуктового склада.

2. Формула Уилсона для многопродуктовой модели.

3. Общая задача с ограничениями: метод множителей Лагранжа

4. Задача с ограничением по среднему уровню запаса

5. Задача с ограничением по стоимости запаса

6. Задача с ограничением затрат на заказы

7. Модель с совместными заказами

Постановка задачи.

Имеется склад для хранения продуктов и выполнены все остальные условия модели Уилсона. Имеется вектор, задающий ежедневный спрос по всем видам продуктов,. Задан вектор констант стоимости заказов и доставки товаров; Вектор констант- удельные затраты по хранению. Требуется рассчитать размеры оптимальных партий по всем видам товаров.

Составляется набор функций затрат Они имеют однотипный вид.

,

(1)

где – искомая величина –объемы партий соответствующего продукта;

–длительность периода планирования;

Составляется общая функция издержек (функция переменных):

(2)

Решается задача нахождения минимума этой функции.

Для удобства, предлагается ввести новые обозначения.

После введения таких обозначений функцию издержек можно записать в следующем виде:

(3)

Координаты критической точки можно найти из условий.

(4)

Получим следующие формулы модели Уилсона.

(5)

Минимальные издержки:

(6)

Эти формулы пригодны для достаточно больших складов, и не содержат никаких ограничений на работу склада. Реальные многопродуктовые склады имеют различные ограничения.

Пусть вектор всех товаров. Будем считать, что у нас есть некоторое количество ограничений.

(7)

Требуется найти минимум функции (3) при дополнительном условии (7). Такие задачи решаются методом множителей Лагранжа.

(8)

Необходимым условием минимума является система уравнений, где кроме частных производных по одной группе переменных содержатся производные по второй группе.

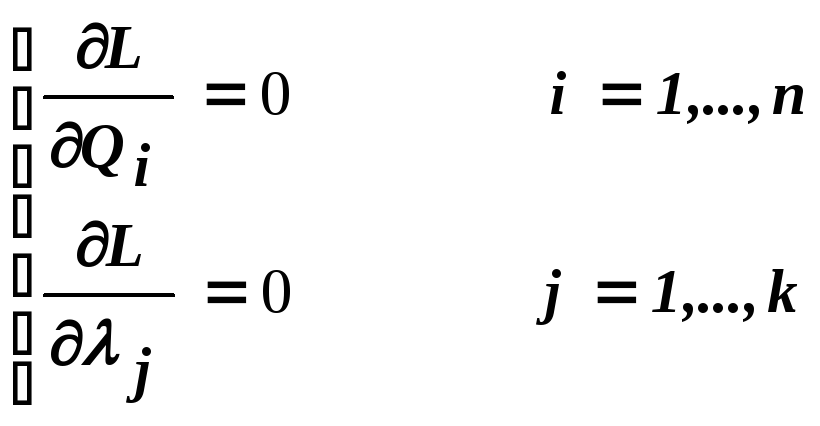
Рассмотрим варианты задач с конкретными видами ограничений:

Ограничение по среднему уровню запаса

Новые константы:

объем склада;

объем единицы товара каждого наименования;

Получаем: объем партий- го товара;

–общий максимальный объем товаров.

Ограничение по среднему уровню запаса:

(9)

Функция Лагранжа:

Частные производные:

Получаем следующие координаты критической точки:

;

(10)

Минимальные издержки:

(11)

По сравнению с задачей без ограничения объемы партий уменьшаются, а издержки увеличиваются.

Ограничение по общей стоимости запаса

Дополнительно введем вектор - цены товаров и подсчитаем максимальную стоимость всех товаров на складе.

,

где поправочный коэффициент (нормировочный множитель), учитывает неравномерность поставок товаров.

Ограничение имеет вид: или.

Составляется функция Лагранжа (удобно вернутся к прежним обозначениям).

(12)

Получаем следующее решение.

(13)

(14)

−отношение двух видов издержек.

Размеры партий уменьшаются, издержки увеличиваются