Модели оперативного календарного планирования

Основная особенность: установление оптимального режима производства во времени (производство отдельных деталей, узлов, режим загрузки оборудования, взаимодействие участков). В общей постановки модели являются сложными.

Общая постановка задачи применительно к машиностроительному производству. Цех (участок) располагает оборудование типов, должно быть обработанодеталей за период. Известны нормы затрат времени на обработку каждых видов деталей на различных видах оборудования и длительность переналадок оборудования при переходе от обработки первой детали к другим. Известны технологические маршруты движения деталей в процессе обработки. Требуется установить такой режим работы каждого вида оборудования и цеха в целом, при которой план-график выпуска готовых изделий будет полностью обеспечен необходимым количеством деталей при минимальной сумме затрат времени (обработка, переналадка, простой оборудования).

Математически эта задача нелинейного программирования с условиями целочисленности для части переменных. В упрощенной постановке получаются частные задачи:

1. технологические маршруты считаются определенными, а размеры партий деталей фиксированными. Требуется определить оптимальную очередность запуска различных деталей в производство. Критерий оптимальный – минимум общего времени обработки всего заданного количества деталей.

2. Для отдельного изделия, потребность в которой не равномерно во времени, требуется определить оптимальный режим производства и хранения. Цель – минимум общих издержек, связанных с неравномерностью графика производства и с хранением запасов.

Имеется видов станков. Требуется обработатьвидов деталей (партий). Для каждой детали задан технологический маршрут – порядок перехода от одного станка к другому. Предположим, что на каждом станке выполняется только одна операция. Требуется определить порядок обработки при минимальных общих затратах от времени. Если–задача о двух станках. Есть два вектора: и,–количество деталей. Предлагается следующий алгоритм решения задачи:

1. все детали нужно разделить на две группы

а)

b)

2) обработка начинается с деталей 1-й группы. Они выстраиваются в порядке возрастания ;

3) детали 2-й группы выстраиваются в порядке убывания .

Пример.

Детали	Время в минутах		Очередность запуска
1	6	2	6
2	3	10	2
3	8	3	5
4	7	5	4
5	4	9	3
6	1	6	1

Алгоритм даёт наилучший вариант из 720 возможных вариантов.

Общая формула метода. Деталь предшествует, если.

Задачи с большим значением значительно усложняются, можно получить приближённые значения для оптимального решения.

Оптимальный режим производства и хранения

Задан плановый период, производится одно изделие (деталь), известна потребность в этой детали ;;– начальный запас на начало периода.

Введём переменные – объем выпуска детали,– запас на конец планового периода.

–прирост;

–снижение;

Получаем следующую систему уравнений:

.

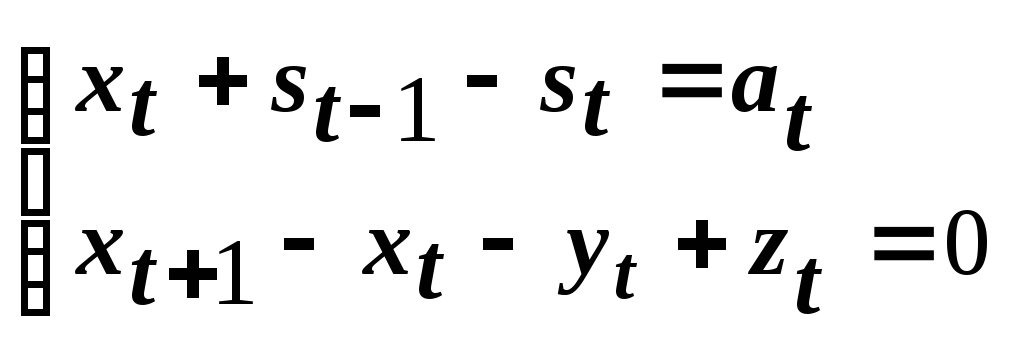Условия: .

Оптимальность режима производства и хранения

или ,

где p, q , – некоторые весовые множители.

Контрольные вопросы:

1. В чем главное отличие задачи приобретения оборудования от аналогичных задач?

2. Каковы главные особенности задач оперативно-календарного планирования?

3. Как формулируется алгоритм решения задачи о двух станках?

4. Каков смысл переменных и целевой функции в задаче расчета оптимального режима производства и хранения?