Задача рационального раскроя материалов

Постановка задачи.

Материалы поступают в виде целых единиц определенных стандартных размеров. Для производственного использования их разрезают на части различных заданных форм и размеров. Необходимо запланировать производство заготовок в определенном количестве с минимумом общих отходов.

Предположим, что из определенного материала необходимо выкроить видов заготовок;– плановые задания,. Известныразличных способов раскроя материалов, для каждого способа известно число– количество заготовок и величина отходов;. Вводим переменные– количество единиц исходного материала запланированное для раскроя данным способом.

.

(10)

Ограничения:

(11)

Условия:

; целые

(12)

Для реального применения данной модели необходимо выполнить соответствующую работу по определению различных способов раскроя. Число этих способов должно быть значительно больше, чем количество видов заготовок. .

Контрольные вопросы.

1. Какова специфика производств, для которых решается задача оптимизации составления смесей и соединений?

2. Что является целевой функцией в задаче оптимизации для производства чугуна?

3. Какова экономическая цель в задаче оптимизации производства бензинов?

4. Каковы ограничения в задаче рационального раскроя материалов?

Лекция 5. Задача приобРеТения оборудования. Модели оперативно−календарного планирования

1. Задача приобретения оборудования.

2. Общая постановка задач оперативно-календарного планирования.

3. Частные случаи задачи. Задача о двух станках.

4. Оптимальный режим производства и хранения.

Задача приобретения оборудования

Постановка задачи.

Требуется приобрести производственное оборудование (станки, машины). Выбор делается из видов оборудования, для которых известна производительность, а также некоторые параметры (цена, занимаемая площадь, количество обслуживаемого персонала и тому подобное). Всегопараметров, задана матрицаих значений.

Задан вектор ресурсов (деньги, общая площадь, численность работников и т.п).

Требуется составить план приобретения оборудования, чтобы в условиях имеющихся ресурсов обеспечить максимальную производительность цеха (участка, отделения).

Введем переменные - количество единиц соответствующего вида оборудования. Составим модель.

(1)

Ограничения:

(2)

Условие неотрицательности:

(3)

Дополнительное условие:

- целые

(4)

Это линейная задача целочисленного программирования, решается с помощью метода Гомори.

Пример.

Выделено 20 тысяч гривен на приобретение оборудования для нового участка, м². Рассматривается два вида оборудования. Машина типа стоит 5 тыс. грн., занимает 8м² и имеет производительность 7 тыс.ед. продукции в смену. Машина типа стоит 2 тыс. грн., занимает 4м², и обеспечивает производство 3 тыс. ед. продукции в смену. Рассчитать оптимальный план приобретения оборудования, которое обеспечит при данных ограничениях максимальную производительность участка.

Введем переменные и– планируемое количество машин. Составим целевую функцию.

Ограничения:

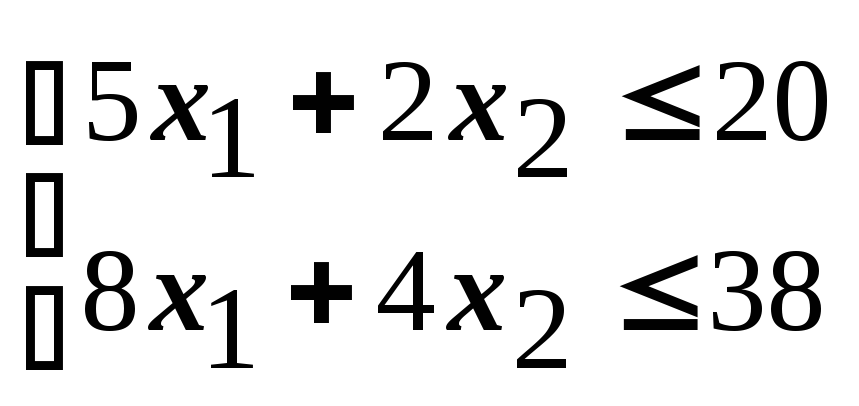
, целые

Решение:

Составим начальный план

Базис	Сб.		A1	A2	A3	A4
x3 x4	0 0	20 38	5 8	2 4	1 0	0 1
Fj - Cj		0	-7	-3	0	0
x1 x2	7 3	1 7,5	1 0	0 1	1 -2	-0,5 1,5
Fj - Cj		29,5	0	0	1	0,5

План оптимален: , но – нецелое.

Метод Гомори: .

Ограничение: .

Новый план почти допустимый, применяется двойственный симплекс–метод. Получаем решение:

–план оптимален.

=29 .

Рекомендуется приобретение 2 машин типа и 5 машин типа, общая производительность участка 29 тыс. ед. в смену. Деньги используются полностью, неиспользованными осталосьм² площади помещения.