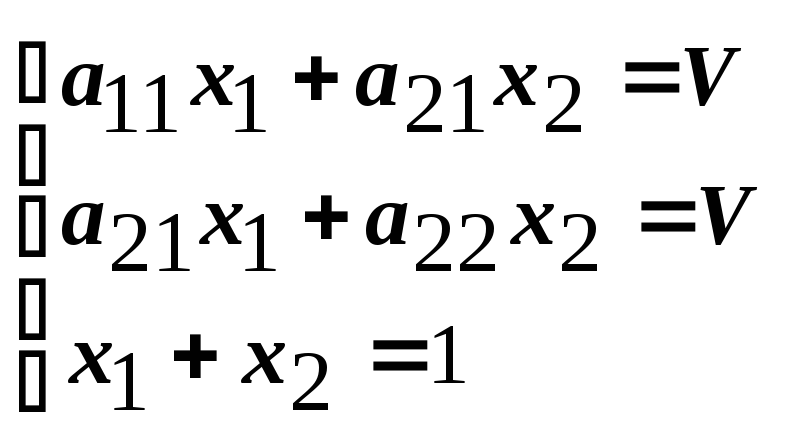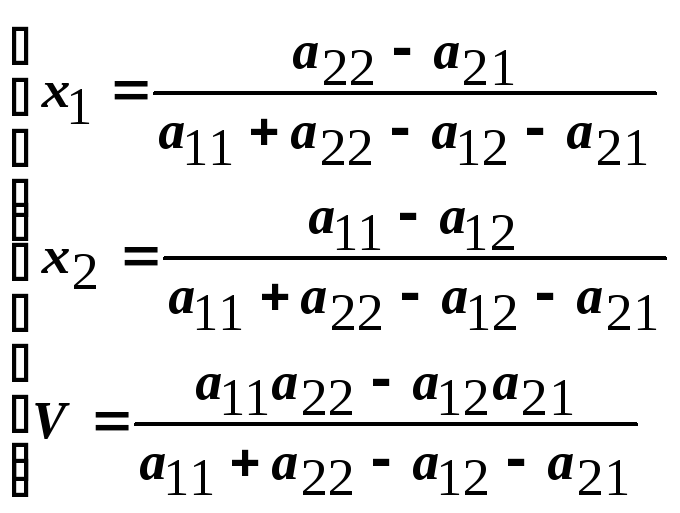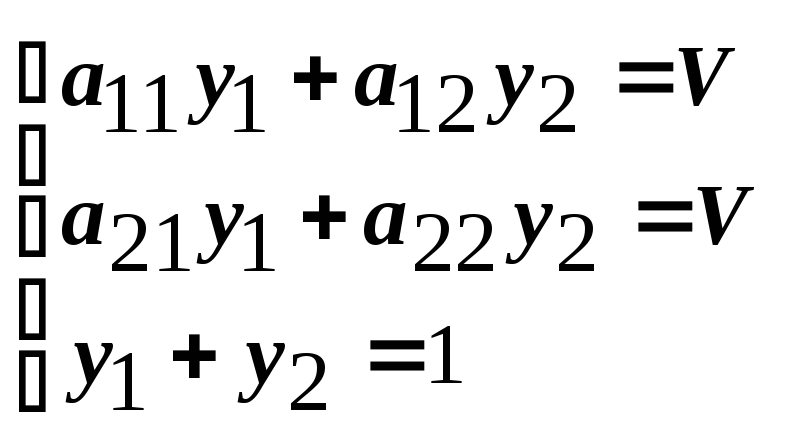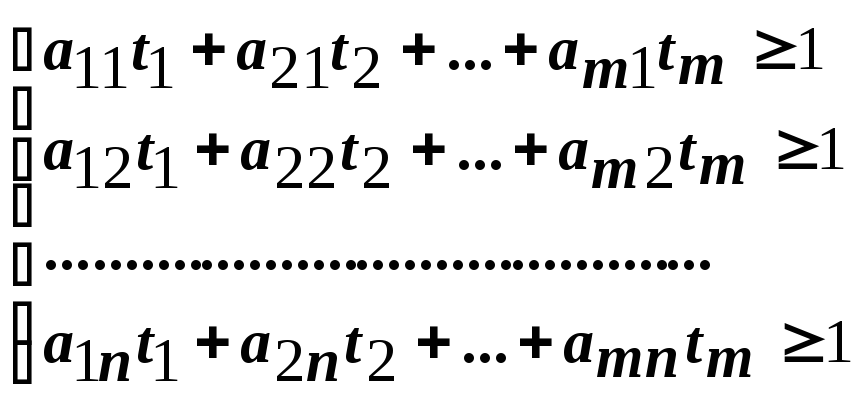Игры в смешанных стратегиях

Если , матрица не содержит седловой точки. Применение минимаксных стратегий обеспечит выигрыш не менееи проигрыш не болеесоответственно. В этом случае говорят о решении игры в смешанных стратегиях: каждый из игроков будет применять несколько стратегий при их случайном выборе.

Введем в рассмотрение два вектора:

;

и - это вероятности, с которой каждый игрок применяет свои первоначальные, чистые стратегии.

Выигрыш при использовании смешанных стратегий определяется как математическое ожидание выигрыша или как средний выигрыш.

переменными являются и.

Выполнено равенство:

(5)

Теорема:

Каждая конечная игра имеет, по крайней мере, одно решение, возможно, в области смешанных стратегий.

- оптимальные вероятности стратегий

–значение игры или цена игры

.

Рассмотрим самый простой частный случай.

; .

Если седловой точки нет, необходимо применять смешанные стратегии. Вводим в рассмотрение 2 вектора вероятностей.

;

(6)

Система линейная, может быть решена любыми способами.

(7)

Вторая система для вероятностей :

(8)

Пример.

Решение игры в смешанных стратегиях

–нижняя цена игры

–верхняя цена игры

Седловой точки нет, так как . Ищем решение игры в смешанных стратегиях.

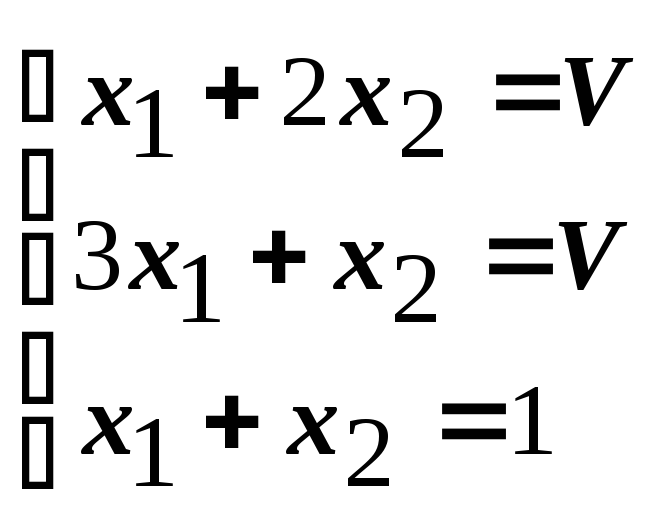
. Аналогично .

Решение игры может быть получено геометрически.

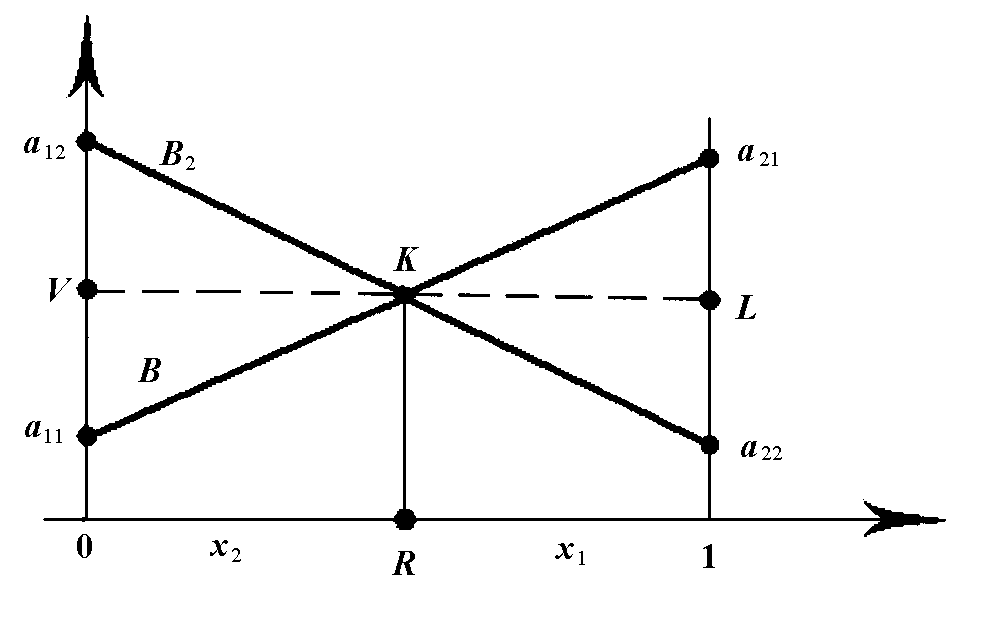
называется нижней границей выигрыша.

Самая верхняя точка определяет решение игры и значения вероятностей.

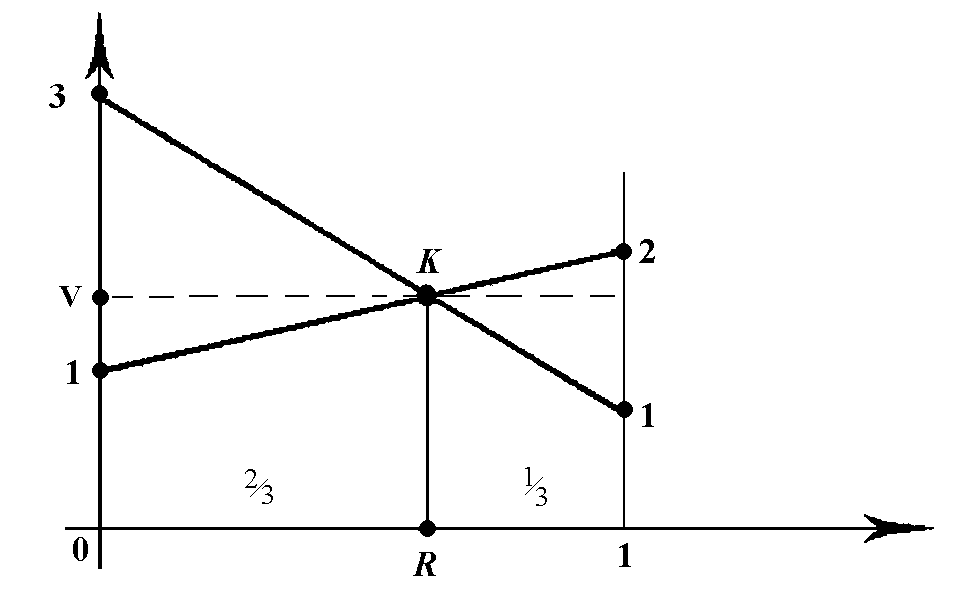
Аналогично может быть геометрически решена игра с матрицей . Результат решения: цена игры; вероятностиии вектор, причем все координатыравны нулю, кроме двух.

Стратегии, которые соответствуют называютактивными стратегиями.

Аналогично можно решать геометрически игру с матрицей . Геометрический метод может быть использован только для нахождения активных стратегий игроков. Для оставшейся квадратной матрицы второго порядка решение может быть найдено аналитически.

Контрольные вопросы

1. Как определяются нижняя и верхняя цены игры?

2. Какие стратегии игроков называются максиминной и минимаксной?

3. Что называется решением игры в смешанных стратегиях?

4. Как решить игру аналитически в случае квадратной матрицы второго порядка?

5. Как геометрически получить решение игры в смешанных стратегиях?

Лекция 15. Сведение матричной игры к задаче линейного программирования

1. Уравнения и неравенства модели

2. Выбор замены переменных, переход к задаче линейного программирования

3. Постановка двойственной задачи

4. Пример военно–тактической игры

Постановка задачи.

Два игрока: и. Игра конечная, имеетсястратегий игрокаистратегий игрока. Задана матрица игры,;; элементы которой являются возможными выигрышами игрока.

Предположим, что матрица не имеет седловой точки, значит . Игра решается в смешанных стратегиях. Векторы вероятностейи.

- решение значения игры.

При правильной игре гарантийный выигрыш первого игрока:

(1)

Для второго игрока:

(2)

Эти неравенства дополняются условиями:

(3)

Предположим, что . Введем новую переменную:

Результат:

(4)

(5)

Надо ввести целевую функцию для получения задачи линейного программирования.

Целевая функция:

(6)

Задачу можно решить симплекс–методом.

В результате найдем вектор и.

Получаем:

,

(7)

Для получается двойственная задача.

Целевая функция:	(8)
Система ограничений:,	(9)

где ;

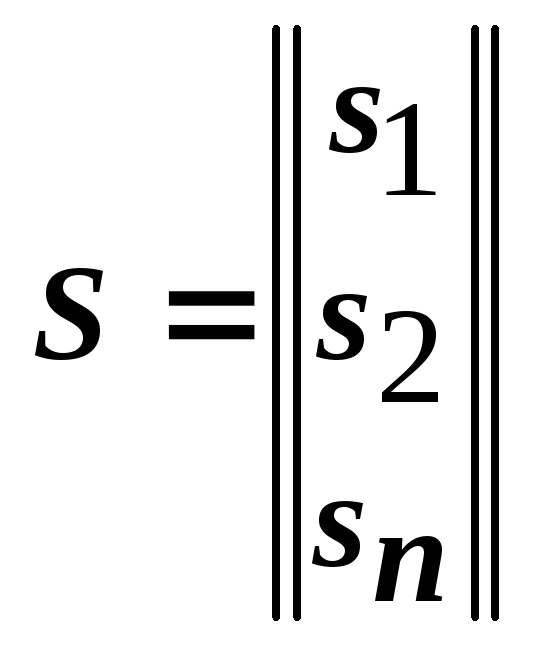
(10)

Задача (8) – (10) является двойственной для задачи (4) – (6) и .

Оптимальный план задачи:

(11)

Если условие не выполнено, необходимо сделать сдвиг в область положительных выигрышей. Для этого, к каждому элементу матрицынеобходимо прибавить одно и тоже положительное число.

.

находится тем же самым способом.

Решение игры получится увеличенным на число :

.

По окончании решения находим и;.

Пример военно-тактической игры.

Две воюющие армии ведут борьбу за 2 пункта. Первая армия состоит из 4-х полков, вторая армия имеет 3 полка. Армия, которая посылает больше полков на тот или другой населенный пункт занимает его и уничтожает все направленные на этот пункт силы противника. Соответствующий игрок получает единицу за занятый пункт и по единице за каждый уничтоженный полк противника. В случае равенства сил, направленных в некоторый пункт, очки не выигрывается.

Цель игры: распределить силы так, чтобы получить максимальный общий выигрыш.

Стратегия каждого игрока будет определяться парой чисел .

–количество войск, посланных на I пункт, – наII пункт.

–стратегии первого игрока .

–стратегии второго игрока .

Матрица игры

	(3;0)	(2;1)	(1;2)	(0;3)
(4;0)	4	2	1	0
(3;1)	1	3	0	-1
(2;2)	-2	2	2	-2
(1;3)	-1	0	3	1
(0;4)	0	1	2	4

;

Целевая функция:

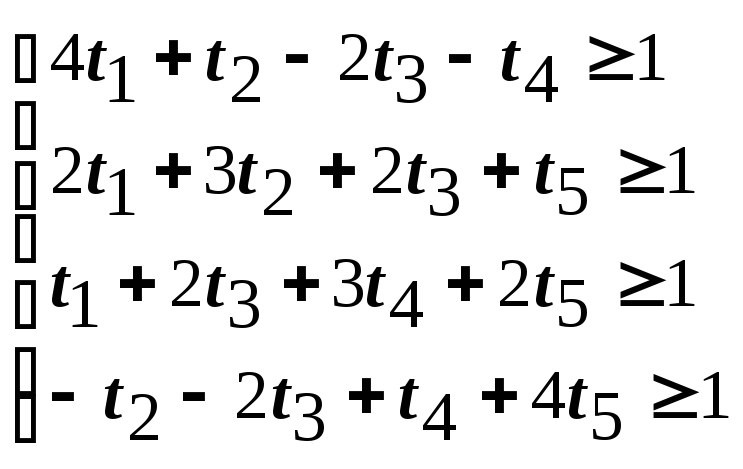
Решение

;

Не рекомендованы второй и четвертый варианты.

Для противника .

Контрольные вопросы

1. Сколько переменных содержит общая математическая модель матричной игры?

2. Каков вид задачи линейного программирования?

3. Как найти решения задач линейного программирования?

4. Как получить решение игры в смешанных стратегиях?