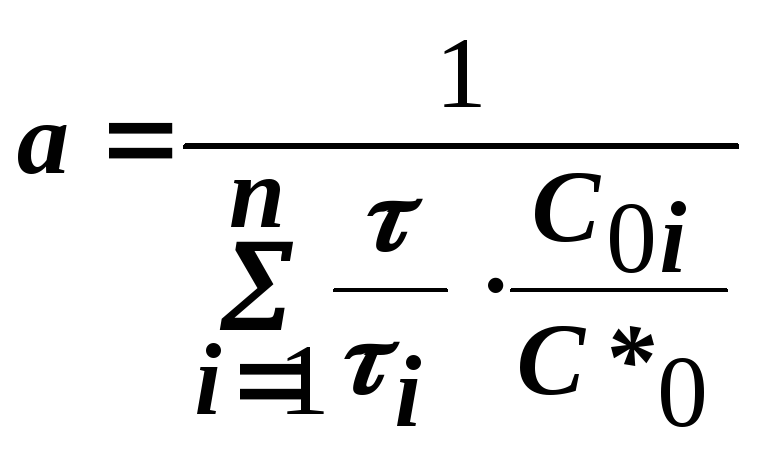- •Лекция 1. Математические модели. Симплекс-метод линейного программирования
- •Построение формализованной схемы
- •Лекция 2. Модели отраслевого планирования
- •Однопродуктовая модель текущего планирования
- •Однопродуктовая задача перспективного планирования
- •Лекция 3. Модели оптимального планирования на промышленном предприятии
- •Расчет оптимальной производственной мощности
- •Расчет оптимальной загрузки оборудования
- •Лекция 4. Модели оптимального планирования на промышленном предприятии
- •Задача оптимизации составления смесей и соединений
- •Задача рационального раскроя материалов
- •Лекция 5. Задача приобРеТения оборудования. Модели оперативно−календарного планирования
- •Задача приобретения оборудования
- •Модели оперативного календарного планирования
- •Оптимальный режим производства и хранения
- •Лекция 6. Динамические модели
- •Задача распределения средств (ресурсов)
- •Задача добычи полезного ископаемого
- •Лекция 7. Модели массового обслуживания
- •Основные понятия теории массового обслуживания
- •Основные элементы системы массового обслуживания
- •Входящий поток требований
- •Обслуживание требований
- •Время обслуживания
- •Лекция 8. Системы массового обслуживания с ожиданием
- •Лекция 9. Системы массового обслуживания с потерями
- •Система массового обслуживания с ограниченной длиной очереди
- •Смо с ограничением на время пребывания в очереди
- •Смо с отказами
- •Лекция 10. Модели управления запасами
- •Лекция 11. Модели управления запасами
- •Однопродуктовая модель с дефицитом
- •Модель с неравномерным спросом
- •Лекция 12. Многопродуктовые модели управления запасами
- •Ограничение по среднему уровню запаса
- •Ограничение по общей стоимости запаса
- •Ограничение затрат на осуществление заказов
- •Модель с совместными заказами
- •Лекция 13. Вероятностные модели управления запасами. Основные понятия теории игр
- •Модели со случайным спросом
- •Основные понятия теории игр
- •Лекция 14. Матричные игры
- •Решение матричной игры
- •Игры в смешанных стратегиях
- •Контрольные вопросы
- •Лекция 15. Сведение матричной игры к задаче линейного программирования
- •Лекция 16. Игры с природой
- •Критерии при решении игр с природой:
- •Список рекомендованой литературы
- •7.050107 "Экономика предприятия)
Ограничение затрат на осуществление заказов
|
|
(15) |
где
Y–
общая стоимость накладных расходов
связанных с размещением заказов на
![]() товаров и их доставкой для одного
планового
периода.
товаров и их доставкой для одного
планового
периода.
|
|
(16) |
Минимальные издержки:
|
|
(17) |
По сравнению с моделью без ограничения, объёмы партий увеличиваются, издержки также увеличиваются.
Модель с совместными заказами
Считаем, что можно производить совместный заказ на несколько товаров, что позволяет уменьшить общие издержки.
Для индивидуальных заказов были получены следующие формулы:
![]()
![]()
![]() ,
,
![]() - интервалы между заказами.
- интервалы между заказами.
|
|
(18) |
Предположим, что
на все товары возможен совместный заказ
с константой
![]() .
Нас интересует
.
Нас интересует![]() –
интервал между заказами.
–
интервал между заказами.
Число заказов
![]() .
.
Общие издержки
заказов:
![]() .
.
Общие издержки:
|
|
(19) |
Точка минимума:
|
|
(20) |
|
|
(21) |
Минимальные издержки при совместном заказе:
|
|
(22) |
Сравнивая издержки при разных системах заказа, можно выбирать так называемую политику (стратегию) заказов.
|
|
(23) |
Если а<1,
выгодны совместные заказы, для
![]() – индивидуальные.
– индивидуальные.
Рассмотрена нелинейная детерминированная многопродуктовая модель управления запасами.
Контрольные вопросы
Какова общая постановка задачи управления запасами для многопродуктового склада?
Как находится оптимальное решение в задаче без ограничений?
Каков общий метод решения задач с ограничениями?
Как находятся оптимальные решения в конкретных задачах с ограничением?
Как влияют ограничения на объемы партий товаров и оптимальные издержки?
Как решается задача с разрешенными совместными заказами?
Лекция 13. Вероятностные модели управления запасами. Основные понятия теории игр
Вероятностные модели управления запасами: основные понятия
Расчет резервного запаса для вероятностной модели
Основные понятия теории игр
Матрица игры
Модели со случайным спросом
Имеется однопродуктовый
склад. Считаем, что спрос
![]() случайный и доставка происходит в
течение некоторого времени;
случайный и доставка происходит в
течение некоторого времени;![]() длительность доставки. В момент
длительность доставки. В момент![]() – должен быть подан заказ, чтобы к
моменту исчерпания запаса заказ был
доставлен.
– должен быть подан заказ, чтобы к
моменту исчерпания запаса заказ был
доставлен.
![]()
![]()
Предположим, что
![]() – случайная величина, для которого
известно среднее значение
– случайная величина, для которого
известно среднее значение![]() ,
тогда
,
тогда![]() .
.
Если подавать
заявку в тот момент, когда на складе
осталось![]() единиц
товара, то в 50% случаев к моменту доставки
товаров запас будет исчерпан.
единиц
товара, то в 50% случаев к моменту доставки
товаров запас будет исчерпан.
Аналогичная
ситуация, если
![]() является случайной величиной с некоторым
средним значением
является случайной величиной с некоторым
средним значением![]()
Чтобы уменьшить вероятность дефицита, необходимо создание резервного запаса, т.е. заказ подаётся тогда, когда имеющийся запас товаров больше средней потребности за среднее время доставки.
![]() - случайная величина,
это потребность в товаре за время его
доставки.
- случайная величина,
это потребность в товаре за время его
доставки.
Будем считать, что
эта величина имеет нормальное
распределение; (![]() )
– параметры нормального закона. Вводим
в рассмотрение коэффициент рискаК
и обозначим через
)
– параметры нормального закона. Вводим
в рассмотрение коэффициент рискаК
и обозначим через
![]() – резервный, страховой запас.
– резервный, страховой запас.
![]() –количество
товара, которое должно быть на складе
в момент заказа.
–количество
товара, которое должно быть на складе
в момент заказа.
|
|
(1) |
Для удобства
расчёта проведём нормирование случайной
величины
![]() .
.
![]()
![]()
![]()
Плотность для этой случайной величины задаётся формулой:
![]()
|
|
(2) |
R(К)
– находится по таблице из условия
![]() .
После этого величину резервного запаса
можно найти по следующей формуле:
.
После этого величину резервного запаса
можно найти по следующей формуле:
|
|
(3) |
Объем партии товара расчитывается по формуле Уилсона.
|
|
(4) |
Издержки увеличатся.
|
|
(5) |
Если отказаться от требования бездефицитности, нужно вводить штрафы за непоставку товаров.

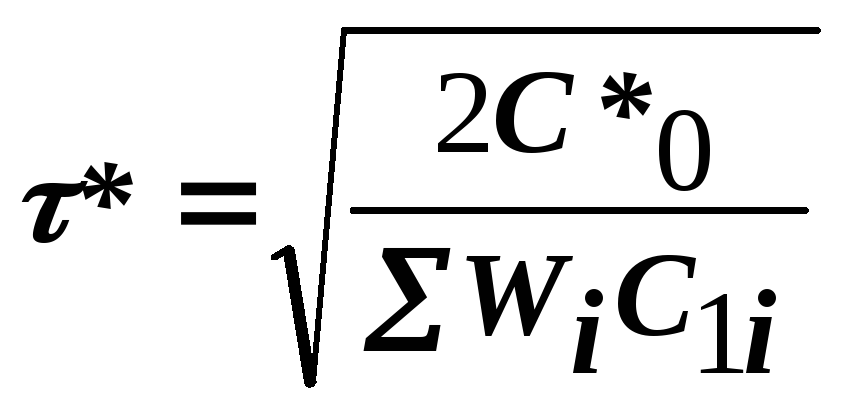

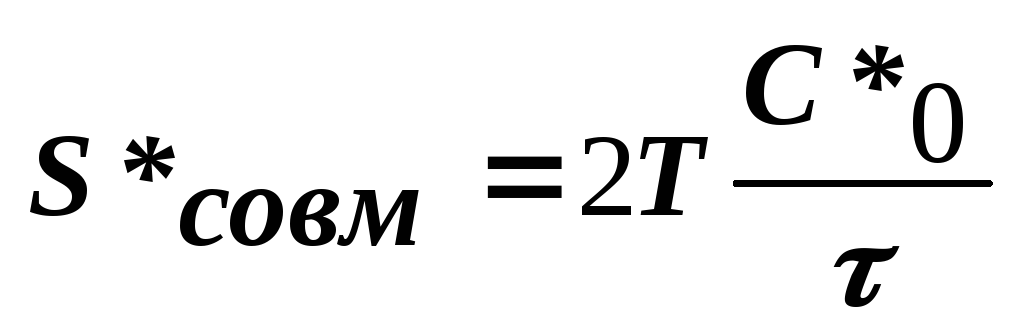
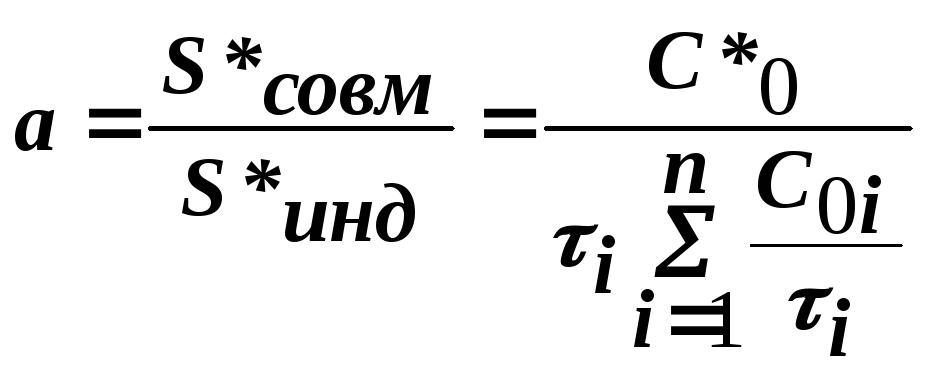 ; или
; или