Лекция 10. Модели управления запасами

1. Общая постановка задачи управления запасами

2. Однопродуктовая модель Уилсона: условия и параметры

3. Оптимальное решение в модели Уилсона и его свойства.

Общая постановки задачи

Имеется некоторый склад для хранения наименований товаров. Известен ежедневный спрос на каждый вид товаровИзвестна общая емкость (объем) склада. Требуется определить процедуру завоза товаров на склад, при которой спрос удовлетворяется и издержки минимальные. Пусть– объемы партий соответствующих товаров. Их сумму обозначим через,

В модели без дефицита издержки двух видов:

1. издержки по заказу и доставке товаров;

2. издержки хранения;

Задача имеет тривиальное решение.

Недостатки этого решения:

1. склад работает как перевалочная база;

2. невозможность реализации решения на практике:

а) для многих видов товаров существуют минимальные объемы партий;

б) общий объем может быть слишком велик для одновременной доставки (транспортное ограничение).

Вывод:для реального работающего склада (оптовый базы) практически невозможен одноразовый завоз по всей номенклатуре товаров.

Формулировка одной из конкретных задач – определить график доставки товаров в такой очередности и в таком количестве, чтобы при безусловном удовлетворении спроса средней объем (уровень) запасов был минимальным.

Математические методы решения подобных задач составляют теорию управления запасами.

Однопродуктовая модель Уилсона:

1. на складе хранится один товар (продукт);

2. спрос на товар является постоянным (уровень запаса товара убывает с постоянной скоростью) ;

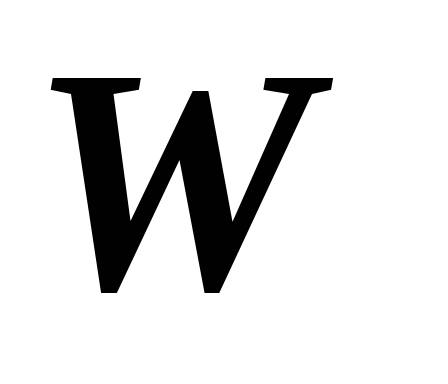3. в той момент, когда запас исчерпан, подается заявка на доставку новой партии товаров;

4. выполнение заявки (заказа) осуществляется мгновенно;

5. накладные расходы, связанные с заказом и доставкой товара постоянны и не зависятот количества товаров (объема партий);

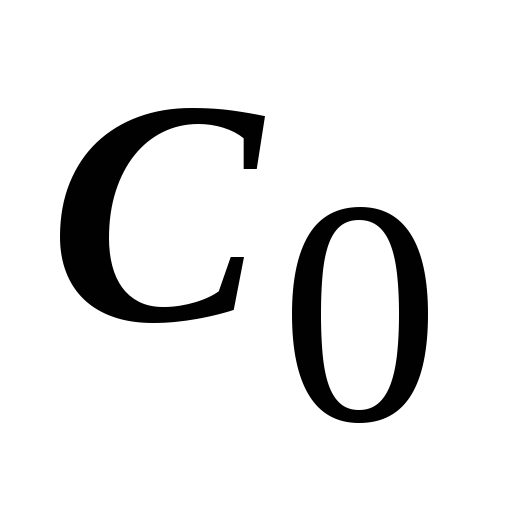6. ежедневная стоимость хранения единицы товара постоянна С₁.

Схема работы склада

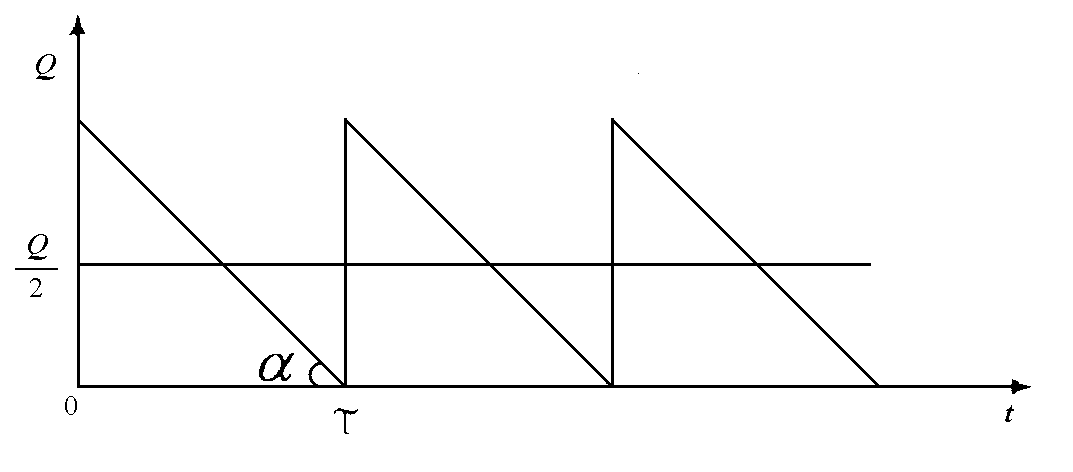
–максимальное количество товара на складе; – время;– интервал между точками заказа.

;

Планируем работу склада на некоторый период Т.

Средний уровень запаса:

Издержки хранения в одном периоде: .

Общие издержки хранения:

Рассчитываем количество заказов: .

Общие издержки по заказу и доставке:

Общие издержки в плановом периоде S:

,

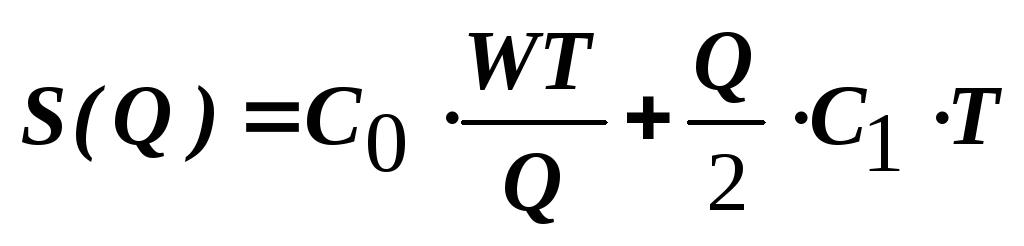
(1)

Найдём минимум составленной функции издержек.

; ;.

Формула Уилсона:

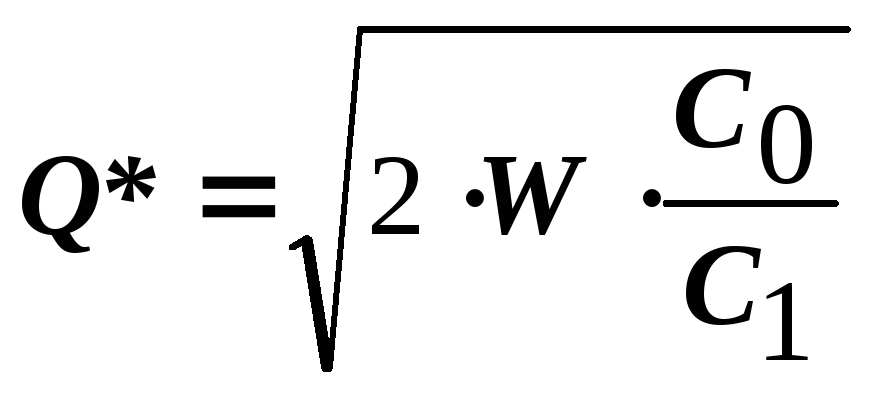
(2)

Можно проверить, что Q* - это точка минимума:

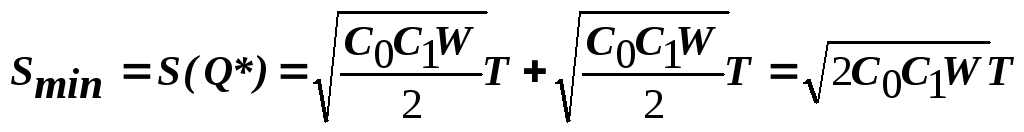
(3)

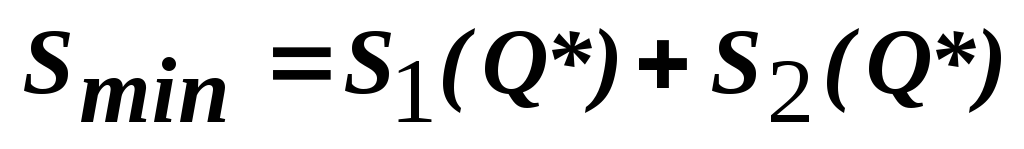
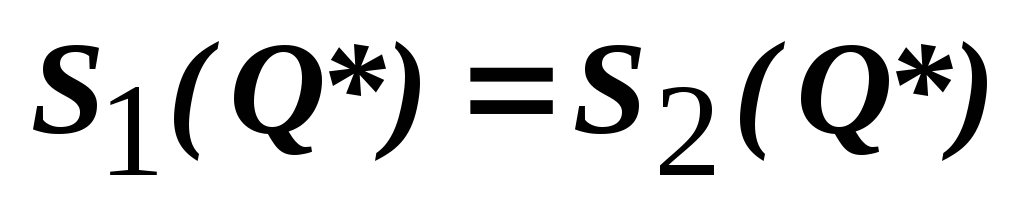
(4)

Вывод: в точке минимума совпадают издержки хранения и издержки заказа и доставки.

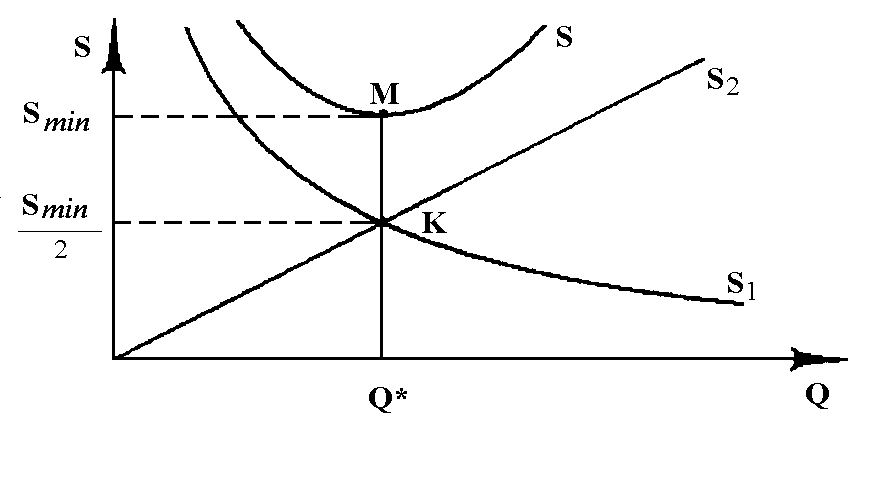
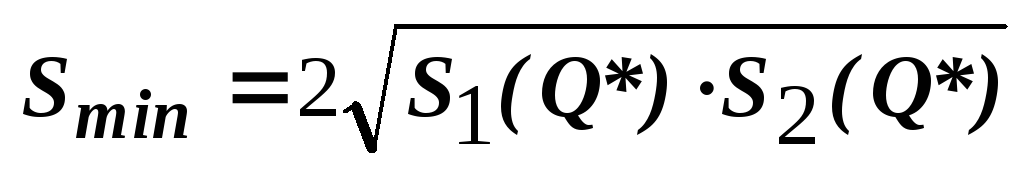
(5)

Найдем интервал между заказами.

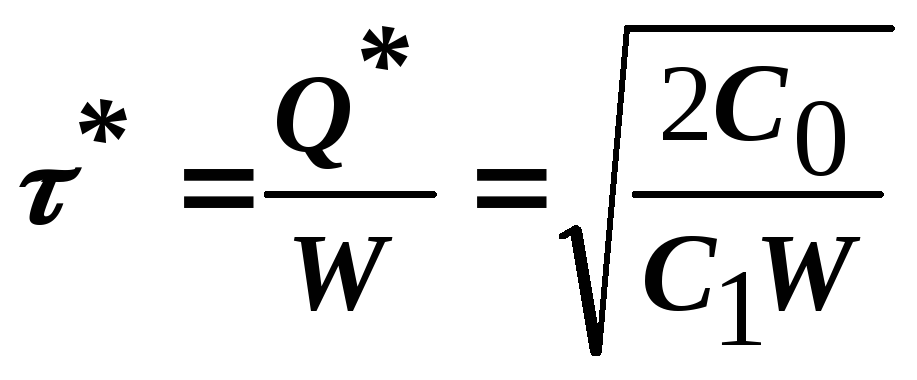
(6)

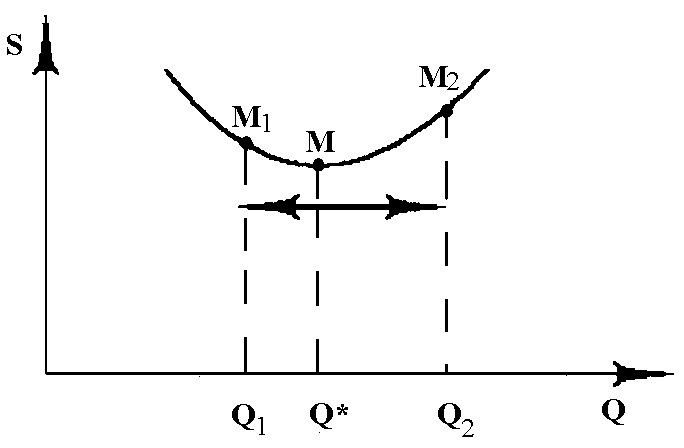
Практические трудности при использовании модели Уилсона:

1. теоретическая оптимальная величина не всегда может быть реализована на практике. Округлениев любую сторону приводит к увеличению издержек по сравнению с минимально теоретически возможными.

2. оптимальное также может быть практически не реализуемым.

Направления усложнения модели Уилсона:

_{1. Модель с дефицитом.}

2. – переменный детерминированный спрос.

3. Модели со случайным спросом

4. Многопродуктовые модели.

Контрольные вопросы.

1. Какова общая постановка задачи управления запасами?

2. Каковы условия модели Уилсона?

3. Из чего состоят общие издержки в этой модели?

4. Какие есть недостатки у оптимального решения задачи?