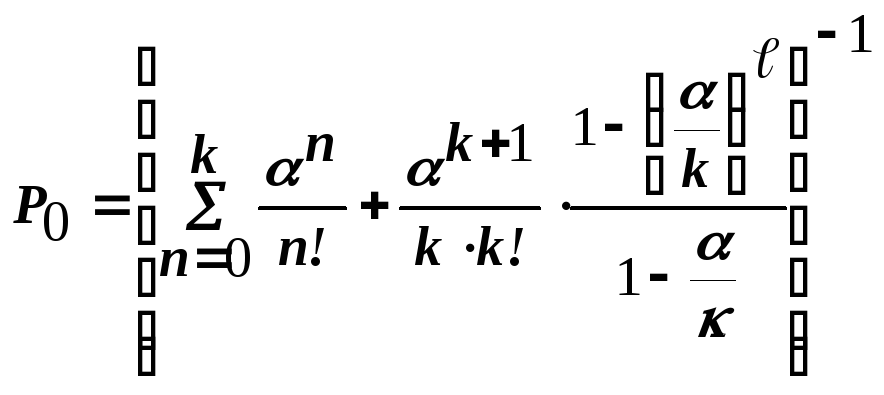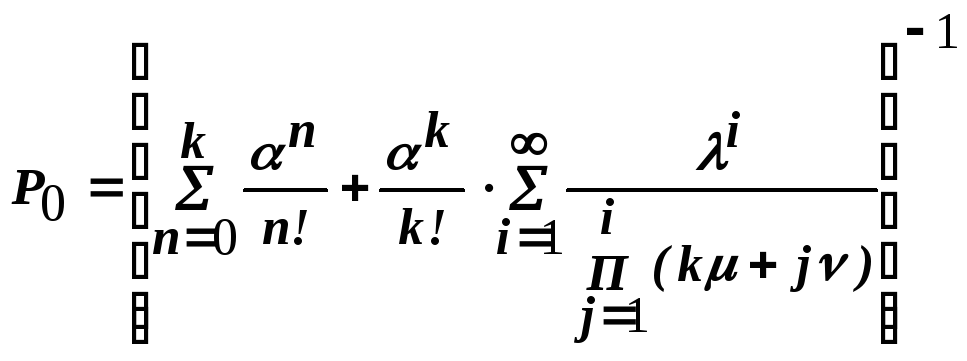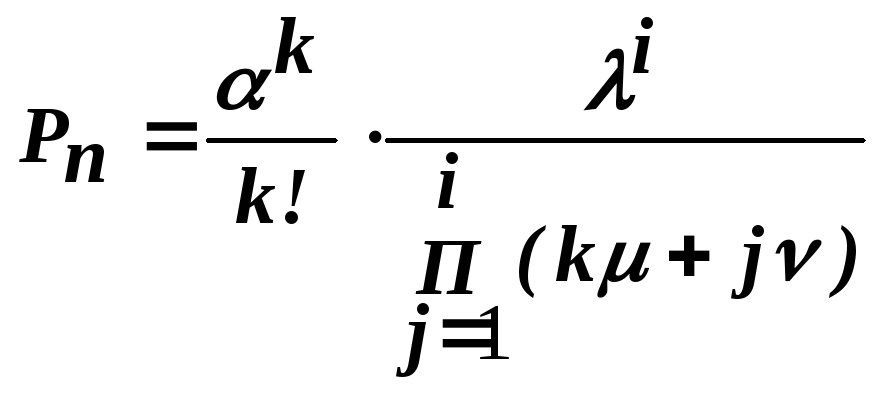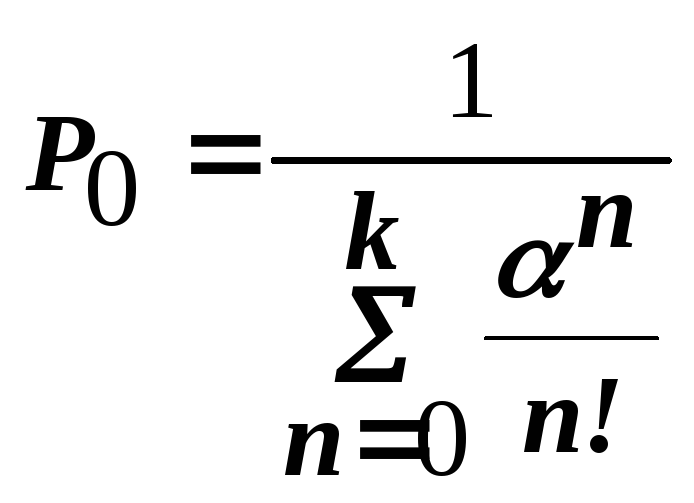- •Лекция 1. Математические модели. Симплекс-метод линейного программирования
- •Построение формализованной схемы
- •Лекция 2. Модели отраслевого планирования
- •Однопродуктовая модель текущего планирования
- •Однопродуктовая задача перспективного планирования
- •Лекция 3. Модели оптимального планирования на промышленном предприятии
- •Расчет оптимальной производственной мощности
- •Расчет оптимальной загрузки оборудования
- •Лекция 4. Модели оптимального планирования на промышленном предприятии
- •Задача оптимизации составления смесей и соединений
- •Задача рационального раскроя материалов
- •Лекция 5. Задача приобРеТения оборудования. Модели оперативно−календарного планирования
- •Задача приобретения оборудования
- •Модели оперативного календарного планирования
- •Оптимальный режим производства и хранения
- •Лекция 6. Динамические модели
- •Задача распределения средств (ресурсов)
- •Задача добычи полезного ископаемого
- •Лекция 7. Модели массового обслуживания
- •Основные понятия теории массового обслуживания
- •Основные элементы системы массового обслуживания
- •Входящий поток требований
- •Обслуживание требований
- •Время обслуживания
- •Лекция 8. Системы массового обслуживания с ожиданием
- •Лекция 9. Системы массового обслуживания с потерями
- •Система массового обслуживания с ограниченной длиной очереди
- •Смо с ограничением на время пребывания в очереди
- •Смо с отказами
- •Лекция 10. Модели управления запасами
- •Лекция 11. Модели управления запасами
- •Однопродуктовая модель с дефицитом
- •Модель с неравномерным спросом
- •Лекция 12. Многопродуктовые модели управления запасами
- •Ограничение по среднему уровню запаса
- •Ограничение по общей стоимости запаса
- •Ограничение затрат на осуществление заказов
- •Модель с совместными заказами
- •Лекция 13. Вероятностные модели управления запасами. Основные понятия теории игр
- •Модели со случайным спросом
- •Основные понятия теории игр
- •Лекция 14. Матричные игры
- •Решение матричной игры
- •Игры в смешанных стратегиях
- •Контрольные вопросы
- •Лекция 15. Сведение матричной игры к задаче линейного программирования
- •Лекция 16. Игры с природой
- •Критерии при решении игр с природой:
- •Список рекомендованой литературы
- •7.050107 "Экономика предприятия)
Лекция 9. Системы массового обслуживания с потерями
СМО с ограниченной длиной очереди
СМО с ограничением на время пребывая в очереди.
СМО с отказами
Система массового обслуживания с ограниченной длиной очереди
Разрешена очередь
с максимальной длиной
![]() .,
.,![]() - число каналов,
- число каналов,![]() - интенсивность потока,
- интенсивность потока,![]() –
интенсивность обслуживания;
–
интенсивность обслуживания;![]() –
напряженность обслуживания.
–
напряженность обслуживания.
Возможное число заявок в системе:
![]() .
.
Максимальное
количество заявок в системе
![]()
Вероятности состояний находим по формулам:
|
|
(1) |
|
|
(2) |
|
|
(3) |
![]() - вероятность
отказа.
- вероятность
отказа.
|
Средняя
длина очереди:
|
(4) |
Пример.
Имеется автозаправка с тремя бензоколонками, площадка ожидания рассчитана на 3 машины. На заправку прибывает в среднем две машины в минуту. Среднее время заправки одной машины – 1 минута. Определить вероятность отказа и среднюю длину очереди.
Решение:
![]()
![]()
![]()
![]() мин.
мин.
![]()
![]()
![]()
![]()
Вероятность состояния "свободно" равна 0,122
![]()
В среднем 5% машин не имеют возможности заправиться.
![]()
Смо с ограничением на время пребывания в очереди
Считаем, что время
ожидания в очереди ограничено случайной
величиной
![]() ,
среднее значение которой
,
среднее значение которой![]() считается известным. Интенсивность
потока требований, покидающих систему
не дождавшись обслуживания.
считается известным. Интенсивность
потока требований, покидающих систему
не дождавшись обслуживания.
![]()
Вероятности состояний системы:
|
|
(5) |
|
|
(6) |
|
|
(7) |
Пропускная
способность
![]()
Пример.
В пункте химчистки имеется 3 аппарата. В среднем в химчистку приходят 6 человек в час. Среднее время обслуживания одного клиента 20 минут. Среднее количество клиентов покидающих очередь, не дождавшись обслуживания – один человек в час. Найти абсолютную пропускную способность пункта химчистки.
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Пропускная способность химчистки:
![]() человек в час.
человек в час.
Смо с отказами
Очередь запрещена,
в системе количество заявок не больше
числа каналов
![]() .
Это самая простая модель, она была
изучена первой.
.
Это самая простая модель, она была
изучена первой.
Число заявок в
системе
![]()
Вероятности состояний
|
|
(8) |
|
|
(9) |
Вероятность отказа:
|
|
(10) |
Дополнительные показатели.
Среднее число занятых каналов.
|
|
(11) |
Среднее число свободных каналов:
|
|
(12) |
Коэффициент занятости:
|
|
(13) |
Коэффициент простоя:
|
|
(14) |
Относительная
пропускная способность:
![]() .
.
Абсолютная
пропускная способность:
![]() .
.
Пример.
Справочная
телефонная служба имеет 3 параллельно
работающих телефона (![]() ),
в некоторый интервал времени поступает
0,5 звонка в минуту, (
),
в некоторый интервал времени поступает
0,5 звонка в минуту, (![]() ).
Интенсивность обслуживания
).
Интенсивность обслуживания![]() звонка в минуту. Рассчитать вероятности
всех состояний и определить коэффициенты
занятости, простоя и пропускную
способность.
звонка в минуту. Рассчитать вероятности
всех состояний и определить коэффициенты
занятости, простоя и пропускную
способность.
Решение:
![]()
![]()
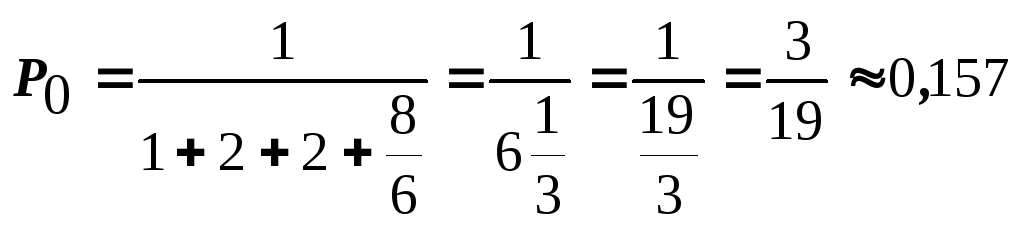
![]()
![]()
![]()
Вероятность отказа
![]() ,
каждый пятый звонок не обслуживается.
,
каждый пятый звонок не обслуживается.
Среднее число занятых каналов:
![]()
Соответственно
![]() ;
;![]() ;
;![]()
![]()
![]() .
.
Контрольные вопросы.
Как описывается в общем виде работа СМО с ограничением на длину очереди?
Какими параметрами задается СМО с этим ограничением?
Как рассчитывается вероятности состояний системы?
Какими параметрами задается СМО с ограничением на время пребывания в очереди?
Каковы характеристики качества обслуживания в этой системе?
Какими параметрами задается СМО с отказами?
Каковы характеристики качества работы этой системы?