2. Движение материальной точки.

Движение происходит в пространстве и времени. Для описания движения надо знать в каких местах пространства оно находилось в разные времена. Положение тела в пространстве можно определить только по отношению к другим телам.

Тело, по отношению к которому определяется положение материальной точки, называется телом отсчета.

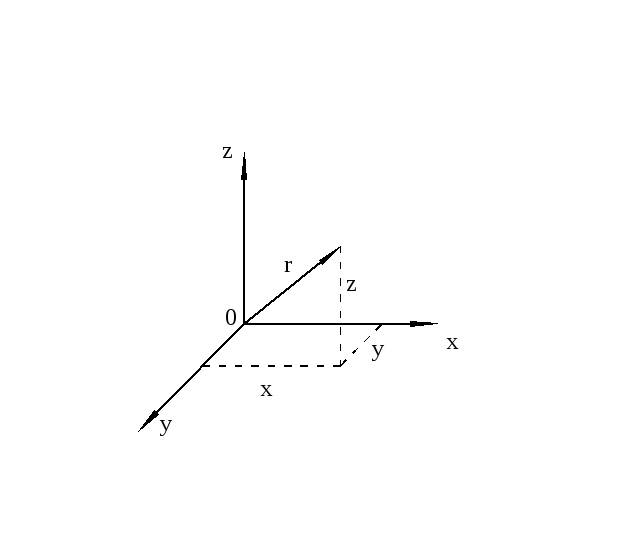
	С ним связывается система отсчета - совокупность координат и часов, связанных с этим телом. В декартовой системе координат положение точки А характеризуется тремя координатами: x,y,zили радиусом вектором, проведенном из начала координат в данную точку. С течением времени координаты точки меняются. В общем случае ее движение определяется системой скалярных уравнений
Рис.2.

(1)

или векторным уравнением

(2)

Уравнения (1) и (2) называются кинематическими уравнениями материальной точки.

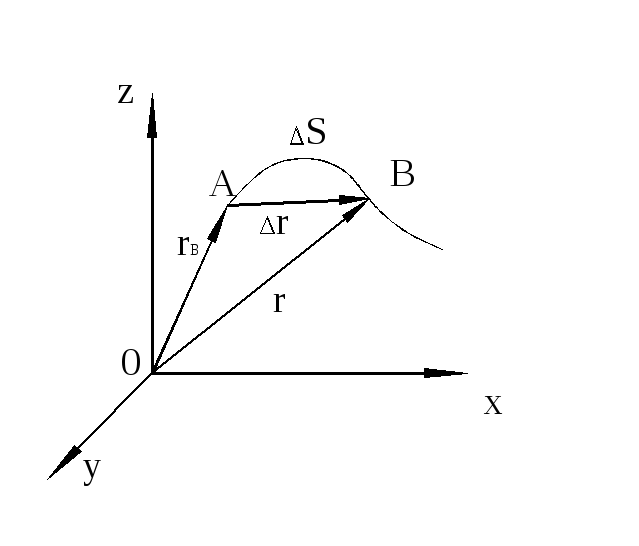
Линия, которую описывает материальная точка в пространстве, называется траекторией.

В зависимости от формы траектории движение может быть прямолинейным или криволинейным. Рассмотрим движение материальной точки по произвольной траектории. Отсчет времени начнем с момента, когда материальная точка находилась в положении А.

	Расстояние, пройденное материальной точкой с момента начала отсчета времени вдоль траектории называется длиной пути или путем dSи является скалярной величиной.Вектор , проведенный из начального положения материальной точки в конечное называется перемещением.Для одного и того же перемещения существуют несколько путей.
Рис. 3.

3. Скорость.

Для характеристики быстроты движения и его направления в данный момент времени вводится векторная величина скорости. В общем случае тело движется в разные моменты времени с разными скоростями. Вектором средней скорости называется отношение приращения вектора к промежутку времени, за которое произошло это перемещение

.

Направлениесовпадает с перемещением. Присредняя скорость стремится к предельному значению, которое называется мгновенной скоростью

.

Средней путевой скоростью называется отношение пути к времени

.

Это скалярная величина. В пределе секущая совпадает с касательной. Мгновенная скорость направлена по касательной к траектории. Средняя скорость и средняя путевая скорость могут существенно различаться. Например, для вращения за период Т =0 и= 0, а =.За полпериодаи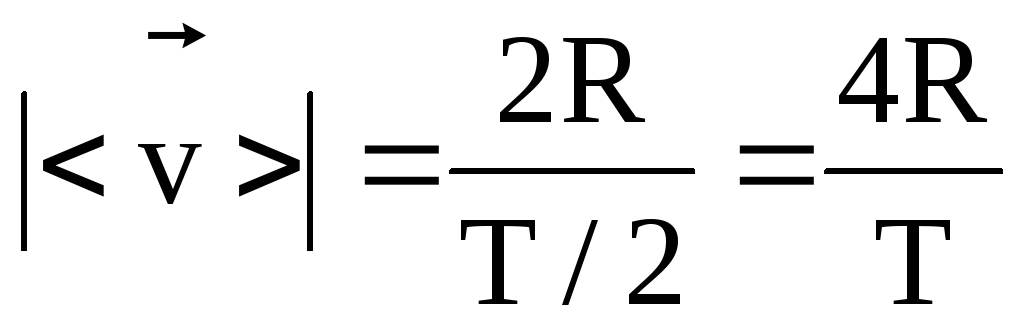, в то время как =.

Средняя скорость зависит от выбранного промежутка времени, а мгновенная от точки на траектории. Если средняя скорость не зависит от промежутка времени. То движение является равномерным и прямолинейным, а средняя скорость совпадает с мгновенной скоростью.

Если только средняя путевая скорость не зависит от , то такое движение называется равномерным.

4. Ускорение.

Физическая величина, характеризующая быстроту изменения скорости по модулю и направлению, называется ускорением.

Мгновенным ускорением называется величина

,

а среднее ускорение равно

.

Так же как и средняя скорость, среднее ускорение зависит от выбранного промежутка , если среднее ускорение не зависит от выбранного промежутка, то есть мгновенное ускорение остается постоянным. То такоедвижение называется равнопеременным с .

Пусть при t= 0 скорость равна, а через времяt-. Тогда, или- закон изменения скорости при равнопеременном движении.

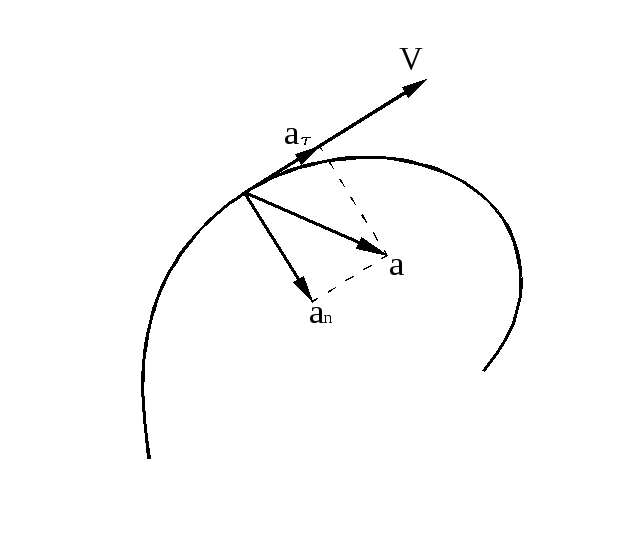
Рассмотрим физический смысл ускорения. Ускорение раскладывают на две составляющие: касательное, или тангенциальное, и нормальное, или центростремительное.

	Величина - отвечает за изменение скорости по абсолютному значению, оно параллельно скорости,- за изменение скорости по направлению, причем , - мгновенная скорость,- радиус кривизны,.
Рис.4.

В зависимости от иускоренные движения можно классифицировать следующим образом:

1) =0,= 0 - равномерное прямолинейное движение,

2) =пост.,= 0 - -прямолинейное равнопеременное движение,

3) =0,= пост. - ,из первого равенства следует, из второго -- это равномерное движение по окружности.

Нахождение переменных по известной зависимости осуществляется по формулам:

Если , то.