- •Федеральное агентство морского и речного транспорта
- •Предисловие
- •Лекция 1. Предмет физики.
- •1. Кинематика. Движение тел.
- •2. Движение материальной точки.
- •3. Скорость.
- •4. Ускорение.
- •5. Вращательное движение. Угловая скорость и угловое ускорение.
- •6. Качение тела.
- •Лекция 2. Динамика материальной точки.
- •1. Первый закон Ньютона.
- •2. Второй закон Ньютона.
- •3. Третий закон Ньютона.
- •4. Закон всемирного тяготения. Сила тяжести. Вес.
- •Силы упругости.
- •Силы трения.
- •Лекция 3. Закон сохранения импульса.
- •Введение.
- •Закон сохранения импульса.
- •Закон движения центра масс.
- •Движение тел с переменной массой. Реактивное движение.
- •Лекция 4. Закон сохранения энергии в механике.
- •Энергия, работа, мощность.
- •Потенциальная энергия.
- •Кинетическая энергия
- •Закон сохранения энергии.
- •Удар абсолютно упругих и абсолютно неупругих тел.
- •Лекция 5. Динамика вращательного движения твердого тела.
- •Вращение твердого тела вокруг неподвижной оси. Кинетическая энергия.
- •2. Момент инерции твердого тела.
- •3. Моменты инерции тел различной формы.
- •4. Момент силы относительно неподвижной точки.
- •5. Момент силы относительно неподвижной оси.
- •6. Момент импульса относительно неподвижной точки.
- •7. Момент импульса относительно неподвижной осиz.
- •Лекция 6. Уравнения динамики вращательного движения.
- •1. Закон сохранения момента импульса.
- •2. Гироскоп.
- •Лекция 7 Колебания и волны.
- •Свободные гармонические колебания. Гармонический осциллятор.
- •Задача о колебании груза на пружине.
- •Задача о физическом маятнике.
- •Задача о математическом маятнике.
- •Скорость и ускорение при гармоническом колебании.
- •Энергия гармонического осциллятора.
- •Лекция 8. Сложение колебаний.
- •Сложение гармонических колебаний одного направления и одной частоты.
- •Биения.
- •Формула для сложения колебаний в общем случае для плоских волн.
- •Вынужденные колебания.
- •Затухающие колебания.
- •Механические волны (упругие волны)
- •Лекция 9 Уравнение плоской гармонической волны.
- •Фронт волны
- •Фазовая скорость.
- •Волновое уравнение.
- •Стоячие волны.
- •Звуковые волны.
- •Лекция 10 Механика жидкости
- •Линии и трубки тока. Неразрывность струи.
- •Уравнение Бернулли.
- •Ламинарное и турбулентное течение.
- •Силы сопротивления при движении тел в жидкостях. Закон Стокса. Число Рейнольдса.
- •Лекция 11 Физические основы молекулярно-кинетической теории газов.
- •1. История.
- •2. Идеальный газ. Параметры состояния газа. Уравнение состояния идеального газа.
- •3. Атомная единица массы (а.Е.М.).
- •4. Свойства идеального газа.
- •5. Уравнение Менделеева-Клапейрона.
- •6. Основное уравнение кинетической теории газов (уравнение Клаузиуса).
- •Лекция 12 Первый закон термодинамики.
- •1. Термодинамические системы (тдс).
- •2. Внутренняя энергия систем.
- •3. Первый закон термодинамики. Термодинамические процессы.
- •4. Работа газа при изменении его объема.
- •5. Теплоемкость.
- •Лекция 13 Термодинамические процессы.
- •1. Изохорный процесс
- •2. Изобарный процесс.
- •3. Изотермический процесс.
- •Лекция 14
- •4. Адиабатический процесс.
- •5. Политропический процесс.
- •Лекция 15 Второе начало термодинамики. Сущность второго начала термодинамики.
- •1. Введение
- •2. Обратимые и необратимые процессы.
- •3. Круговые процессы (циклы).
- •4. Прямой цикл (тепловая машина).
- •5. Обратный цикл (холодильник).
- •6. Цикл Карно. Произвольный обратимый цикл.
- •Лекция 16 Энтропия.
3. Первый закон термодинамики. Термодинамические процессы.
Внутренняя энергия термодинамической
системы изменяется за счет совершения
над телом работы
![]() и сообщения ему количества теплоты
и сообщения ему количества теплоты![]() .
Соверщение работы сопровождается
перемещением внешних тел, воздействующих
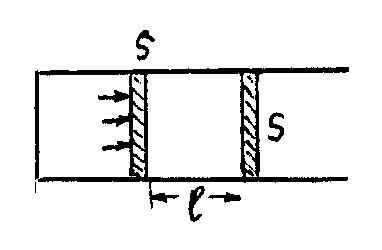
на систему. Так как, например, внутреннюю
энергию газа можно изменить вдвигая
поршень в цилиндр с газом. Поршень
перемещаясь совершает над газом работу
.
Соверщение работы сопровождается
перемещением внешних тел, воздействующих
на систему. Так как, например, внутреннюю
энергию газа можно изменить вдвигая
поршень в цилиндр с газом. Поршень
перемещаясь совершает над газом работу![]() .
По третьему закону Ньютона газ совершает
работу над поршнем
.
По третьему закону Ньютона газ совершает
работу над поршнем![]() =-
=-![]() .
.
Сообщение газу количества теплоты не связано с перемещением внешних тел, то есть макроскопической работой. В этом случае молекулы более нагретого тела совершают работу над молекулами менее нагретого тела.
Совокупность микроскопических процессов захватывающих не все тело, а отдельные его молекулы, приводящих к передаче энергии от тела к телу, носит название теплопередачи.
Количество энергии, переданной от тела к телу посредством теплопередачи, называется количеством теплоты.
Изменение внутренней энергии системы равно
![]() (1)
(1)
![]() и
и![]() - начальное и конечное значение внутренней
энергии системы. Обычно вместо работы,
совершаемой над системой, рассматривают
работу, совершаемую системой над внешним
телом, то есть
- начальное и конечное значение внутренней
энергии системы. Обычно вместо работы,
совершаемой над системой, рассматривают
работу, совершаемую системой над внешним
телом, то есть![]() =-
=-![]() .
Тогда
.
Тогда
![]() (2)
(2)
- количество теплоты, сообщенной системе, идет на приращение внутренней энергии и работу системы над внешними телами.
Это не означает, что теплота всегда идет
на увеличение внутренней энергии.
Бывает, что
![]() >
>![]() .
В этом случае
.
В этом случае![]()
![]() ,
то есть работа совершается за счет
,
то есть работа совершается за счет![]() и убыли внутренней энергии. Если
и убыли внутренней энергии. Если![]() ,
то система не получает тепло, а отдает.
,
то система не получает тепло, а отдает.
Из (2) следует, что
![]() измеряется в тех же единицах, что и
измеряется в тех же единицах, что и![]() и
и![]() ,
то есть в Джоулях.
,
то есть в Джоулях.
Для бесконечно малых изменений систем уравнение (2) можно заменить на дифференциальное
![]() ,
,
![]() - является полным дифференциалом, то
есть изменение его зависит от начального
и конечного состояний и не зависит от
пути, по которому совершается переход;
- является полным дифференциалом, то
есть изменение его зависит от начального
и конечного состояний и не зависит от
пути, по которому совершается переход;![]() и
и![]() зависят от пути перехода системы от
одного состояния к другому и не являются
полными дифференциалами и функциями
состояния. При круговом процессе
зависят от пути перехода системы от
одного состояния к другому и не являются
полными дифференциалами и функциями
состояния. При круговом процессе![]() .
Тогда
.
Тогда![]() ,
то естьнельзя построить периодически
действующий двигатель, который совершал
бы работу, большую, чем сообщенное ему
количество теплоты
,
то естьнельзя построить периодически
действующий двигатель, который совершал
бы работу, большую, чем сообщенное ему
количество теплоты
![]() .
То есть невозможен вечный двигатель
первого рода.
.
То есть невозможен вечный двигатель
первого рода.
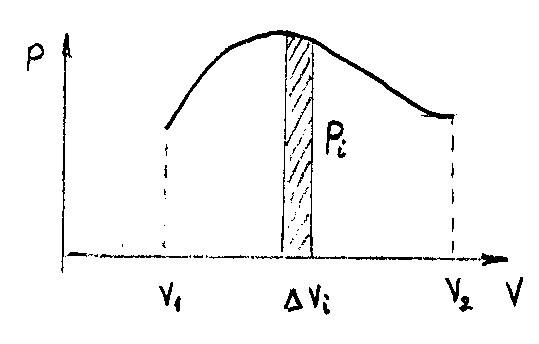
4. Работа газа при изменении его объема.
Найдем работу газа при изменении его объема.
|
|
-работа
зависит от
|
|
Рис.2. |
|
Изобразим процесс изменения объема
рабочего тела на диаграмме (![]() ,
,![]() ).
).
|
|
При изменении объема на
Площадь
между
|
|
Рис. 3. |
|
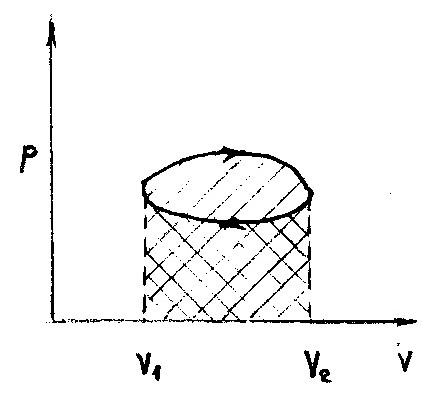
|
|
Работа при круговом процессе будет равна площади, охватываемой круговым циклом. |
|
Рис.4. |
|
5. Теплоемкость.
Теплоемкость равна
![]()
![]() .
(5)
.
(5)
Молярная теплоемкость
![]() ,
,![]() ,
(6)
,
(6)
![]() - число молей.
- число молей.
Удельная теплоемкость
![]() ,
,![]() (7)
(7)
- теплоемкость на кг вещества.
![]() .
(8)
.
(8)
Запишем первое начало термодинамики, учитывая (6) для моля газа, если
![]()
![]() (9)
(9)
- 1-закон термодинамики.
Если нагревание идет при
![]() то работа не совершается и
то работа не совершается и
![]() (10)
(10)
![]() - молярная теплоемкость при постоянном
объеме,
- молярная теплоемкость при постоянном
объеме,![]() ,
,![]() .
Отсюда получаем
.
Отсюда получаем
![]() (11)
(11)
Если нагревание происходит при
![]() ,
то
,
то
![]()
![]() .
.
Однако
![]() .
.
Теперь имеем
![]()
- уравнение Майера.
Физический смысл
![]() - работа, которую совершает 1 моль
идеального газа при нагревании на 1 К
при
- работа, которую совершает 1 моль
идеального газа при нагревании на 1 К
при![]() .
.
Действительно,
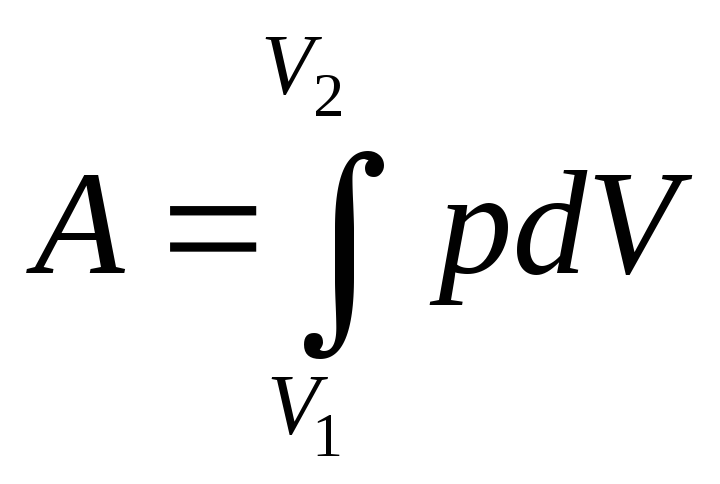 =
=![]() =
=![]() ,
,
так как
![]() и
и![]() .
Отсюда
.
Отсюда
![]() .
.

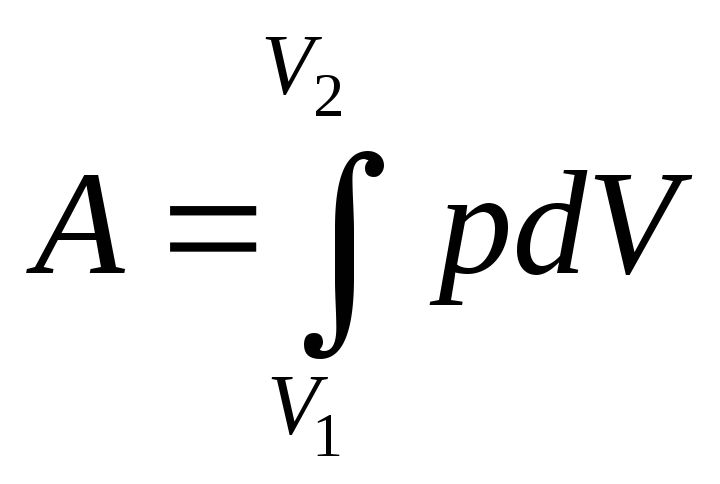 (4)
(4)