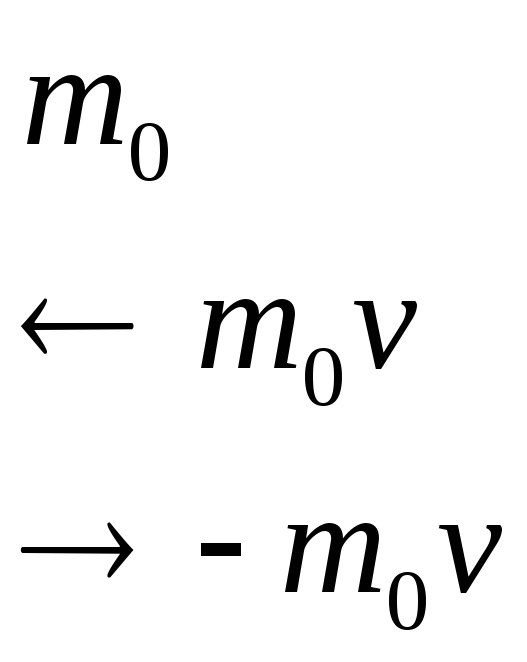- •Федеральное агентство морского и речного транспорта
- •Предисловие
- •Лекция 1. Предмет физики.
- •1. Кинематика. Движение тел.
- •2. Движение материальной точки.
- •3. Скорость.
- •4. Ускорение.
- •5. Вращательное движение. Угловая скорость и угловое ускорение.
- •6. Качение тела.
- •Лекция 2. Динамика материальной точки.
- •1. Первый закон Ньютона.
- •2. Второй закон Ньютона.
- •3. Третий закон Ньютона.
- •4. Закон всемирного тяготения. Сила тяжести. Вес.
- •Силы упругости.
- •Силы трения.
- •Лекция 3. Закон сохранения импульса.
- •Введение.
- •Закон сохранения импульса.
- •Закон движения центра масс.
- •Движение тел с переменной массой. Реактивное движение.
- •Лекция 4. Закон сохранения энергии в механике.
- •Энергия, работа, мощность.
- •Потенциальная энергия.
- •Кинетическая энергия
- •Закон сохранения энергии.
- •Удар абсолютно упругих и абсолютно неупругих тел.
- •Лекция 5. Динамика вращательного движения твердого тела.
- •Вращение твердого тела вокруг неподвижной оси. Кинетическая энергия.
- •2. Момент инерции твердого тела.
- •3. Моменты инерции тел различной формы.
- •4. Момент силы относительно неподвижной точки.
- •5. Момент силы относительно неподвижной оси.
- •6. Момент импульса относительно неподвижной точки.
- •7. Момент импульса относительно неподвижной осиz.
- •Лекция 6. Уравнения динамики вращательного движения.
- •1. Закон сохранения момента импульса.
- •2. Гироскоп.
- •Лекция 7 Колебания и волны.
- •Свободные гармонические колебания. Гармонический осциллятор.
- •Задача о колебании груза на пружине.
- •Задача о физическом маятнике.
- •Задача о математическом маятнике.
- •Скорость и ускорение при гармоническом колебании.
- •Энергия гармонического осциллятора.
- •Лекция 8. Сложение колебаний.
- •Сложение гармонических колебаний одного направления и одной частоты.
- •Биения.
- •Формула для сложения колебаний в общем случае для плоских волн.
- •Вынужденные колебания.
- •Затухающие колебания.
- •Механические волны (упругие волны)
- •Лекция 9 Уравнение плоской гармонической волны.
- •Фронт волны
- •Фазовая скорость.
- •Волновое уравнение.
- •Стоячие волны.
- •Звуковые волны.
- •Лекция 10 Механика жидкости
- •Линии и трубки тока. Неразрывность струи.
- •Уравнение Бернулли.
- •Ламинарное и турбулентное течение.
- •Силы сопротивления при движении тел в жидкостях. Закон Стокса. Число Рейнольдса.
- •Лекция 11 Физические основы молекулярно-кинетической теории газов.
- •1. История.
- •2. Идеальный газ. Параметры состояния газа. Уравнение состояния идеального газа.
- •3. Атомная единица массы (а.Е.М.).
- •4. Свойства идеального газа.
- •5. Уравнение Менделеева-Клапейрона.
- •6. Основное уравнение кинетической теории газов (уравнение Клаузиуса).
- •Лекция 12 Первый закон термодинамики.
- •1. Термодинамические системы (тдс).
- •2. Внутренняя энергия систем.
- •3. Первый закон термодинамики. Термодинамические процессы.
- •4. Работа газа при изменении его объема.
- •5. Теплоемкость.
- •Лекция 13 Термодинамические процессы.
- •1. Изохорный процесс
- •2. Изобарный процесс.
- •3. Изотермический процесс.
- •Лекция 14
- •4. Адиабатический процесс.
- •5. Политропический процесс.
- •Лекция 15 Второе начало термодинамики. Сущность второго начала термодинамики.
- •1. Введение
- •2. Обратимые и необратимые процессы.
- •3. Круговые процессы (циклы).
- •4. Прямой цикл (тепловая машина).
- •5. Обратный цикл (холодильник).
- •6. Цикл Карно. Произвольный обратимый цикл.
- •Лекция 16 Энтропия.
2. Идеальный газ. Параметры состояния газа. Уравнение состояния идеального газа.
Простейшим объектом исследования идеальный газ. Идеальным газом называется газ, молекулы которого имеют пренебрежимо малый размер и не взаимодействуют на расстоянии. А при столкновениях взаимодействуют, как абсолютно упругие шары. Идеальный газ – абстракция. Но это понятие полезное, так как упрощает инженерные расчеты тепловых машин и процессов в них происходящих.
Основными параметрами газа, характеризующими
его состояние являются объем,
![]() ,
давление,
,
давление,![]() ,
и температура,
,
и температура,![]() .
.
3. Атомная единица массы (а.Е.М.).
Массы молекул очень малы,
![]() 10-27кг. Поэтому для характеристики масс
атомов и молекул применяют величины,
получившие название атомной единицы
массы элемента или молекулы,
10-27кг. Поэтому для характеристики масс
атомов и молекул применяют величины,
получившие название атомной единицы
массы элемента или молекулы,
1а.е.м. = 1,67 10-27кг =![]() .
.
Массы всех атомов и молекул измеряют в а.е.м.:
![]() =
12 а.е.м.,
=
12 а.е.м.,![]() = 14 а.е.м.,
= 14 а.е.м.,![]() = 16 а.е.м.
= 16 а.е.м.
Относительной молекулярной (![]() )
или атомной (
)
или атомной (![]() )
массой называется отношение массы
молекулы или атома к (1/12) массы атома
углерода
)
массой называется отношение массы
молекулы или атома к (1/12) массы атома
углерода![]() .
.
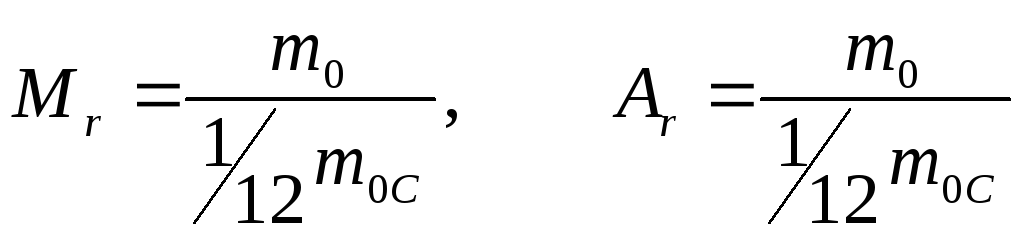
Как видно из определения
![]() - безразмерные величины. Единица массы,
равная (1/12) массы атома углерода
- безразмерные величины. Единица массы,
равная (1/12) массы атома углерода![]() называется атомной единицей массы.
(а.е.м.). Обозначим эту единицу (то есть
а.е.м.), выраженную в килограммах через
называется атомной единицей массы.
(а.е.м.). Обозначим эту единицу (то есть
а.е.м.), выраженную в килограммах через![]() .
Тогда масса атома будет равна
.
Тогда масса атома будет равна![]() ,
а масса молекулы -
,
а масса молекулы -![]() .
.
Количество вещества, которое содержит
число частиц (атомов или молекул), равное
числу атомов в 0,012 кг изотопа
![]() ,
называется молем.
,
называется молем.
Число частиц, содержащихся в моле
вещества называется числом Авогадро,
![]() = 6,022 1023моль-1. Массу моля
называют молярной массой,
= 6,022 1023моль-1. Массу моля
называют молярной массой,
![]() (1)
(1)
В случае углерода
![]()
![]() (кг),
(2)
(кг),
(2)
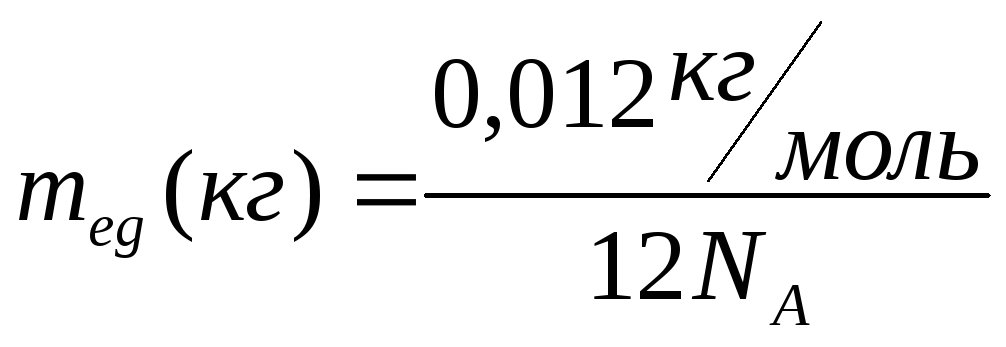 = 1,66 10-27кг.
= 1,66 10-27кг.
Из (2) следует, что
![]() = 0,001 кг/моль.
(3)
= 0,001 кг/моль.
(3)
Подставляя (3) в (1), имеем
![]() = 0,001
= 0,001![]() кг/моль
кг/моль
или
![]() =
=![]() г/моль.
г/моль.
Таким образом, масса моля, выраженная в граммах, численно равна относительной молекулярной массе.
![]() = 12а.е.м.
= 12а.е.м.![]()
![]() = 12 г/моль,
= 12 г/моль,
![]() = 16а.е.м.
= 16а.е.м.![]()
![]() = 16 г/моль,
= 16 г/моль,
![]() = 32а.е.м.
= 32а.е.м.![]()
![]() = 32 г/моль.
= 32 г/моль.
4. Свойства идеального газа.
Размеры молекул порядка 1 А =10-10м.
Давление равно силе, действующей
перпендикулярно на единичную площадку,
![]() .
Давление в СИ измеряется в Па (паскалях).
Па = н/м2, 1 кг/см2= 1 атм = 9,8 104Па, 1 мм рт.ст. = 133 Па.
.
Давление в СИ измеряется в Па (паскалях).
Па = н/м2, 1 кг/см2= 1 атм = 9,8 104Па, 1 мм рт.ст. = 133 Па.
5. Уравнение Менделеева-Клапейрона.
При небольших плотностях газы подчиняются уравнению
![]()
- уравнение состояния идеального газа
Менделеева-Клапейрона,
![]() - число молей,
- число молей,![]() = 8,31 Дж/моль К. Можно уравнению придать
другой вид, если ввести величины
= 8,31 Дж/моль К. Можно уравнению придать
другой вид, если ввести величины
![]() = 1,38 10-23Дж/К:
= 1,38 10-23Дж/К:
![]() .
.
Если
![]() - концентрация частиц, то
- концентрация частиц, то
![]() .
.
Если
![]() ,
то
,
то
![]() .
.
Это выражение используется в аэродинамике.
6. Основное уравнение кинетической теории газов (уравнение Клаузиуса).
Основное уравнение молекулярно кинетической теории связывает параметры состояния газа с характеристиками движения молекул.
Для вывода уравнения используется
статистический метод, то есть зная
характеристики отдельных молекул газа
![]() (концентрация)
можно найти
(концентрация)
можно найти![]() - давление газа, характеристику всего
газа.
- давление газа, характеристику всего
газа.
Для вывода уравнения рассмотрим
одноатомный идеальный газ. Молекулы
движутся хаотически. Скорости молекул
разные. Предположим, что число взаимных
столкновений между молекулами газа
пренебрежимо мало по сравнению с числом
ударов о стенки сосуда, соударения
молекул со стенками сосуда абсолютно
упруги. Найдем давление на стенки
сосуда, предположив, что газ находится
в сосуде кубической формы с ребром
![]() .
Давление ищем как усредненный результат
ударов молекул газа о стенки сосуда.
.
Давление ищем как усредненный результат
ударов молекул газа о стенки сосуда.
|
|
Изменение импульса молекулы за счет столкновения со стенкой равно
|
|
|
|
1). По третьему закону Ньютона стенка
получает импульс от каждой молекулы
![]()
2). За время
![]() площадки
площадки![]() достигают
только те молекулы, которые заключены
в объеме
достигают
только те молекулы, которые заключены
в объеме
![]()
3). Число этих молекул в объеме
![]() равно
равно
![]() .
.
4). Число ударов о площадку равно
![]() .
.
5). При столкновении молекулы передают площадке импульс
![]()
Учитывая, что![]() - сила, а
- сила, а![]() - давление,
- давление,
имеем для давления
![]() (1)
(1)
Если в объеме газ содержит
![]() молекул, которые движутся со скоростями
молекул, которые движутся со скоростями![]() ,
то надо ввести понятие о среднеквадратичной
скорости по формуле
,
то надо ввести понятие о среднеквадратичной
скорости по формуле
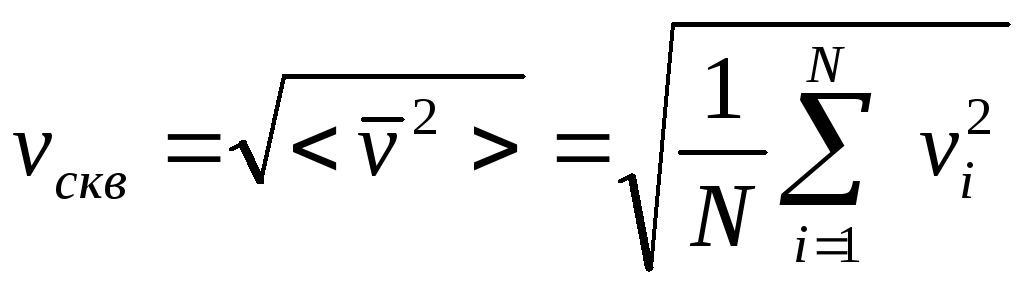 .
(2)
.
(2)
Тогда выражение (1) примет вид
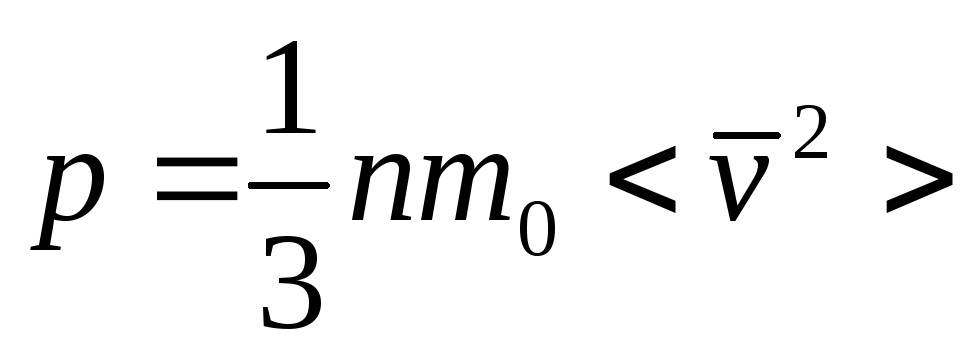 =
=![]()
- Основное уравнение кинетической теории газов.
Это уравнение можно преобразовать, замечая, что
![]() .
.
Тогда
![]() .
.
С другой стороны
![]() .
.
Поэтому
![]() .
.
Средняя кинетическая энергия хаотического
движения молекул прямо пропорциональна
температуре и не зависит от массы. При
Т=0
![]() = 0, движение молекул газа прекращается
и давление равно нулю.
= 0, движение молекул газа прекращается
и давление равно нулю.
Абсолютная температура, Т – это мера средней кинетической энергии поступательного движения молекул идеального газа. Но это верно лишь при умеренных температурах, пока нет распада или ионизации молекул и атомов. Если число частиц в системе мало, то это тоже неверно, так как нельзя ввести понятие средней квадратичной скорости.
Из
![]() и
и![]() следует
следует
![]() =
=![]() .
.