Лекция 10 Механика жидкости

1. Линии и трубки тока. Неразрывность струи.

При изучении жидкостей их рассматривают как сплошную непрерывную среду, не вдаваясь в молекулярное строение жидкостей. При описании движения жидкости проще следитьне за частицами жидкости, аза отдельными точками пространстваи отмечать скорость, с которой проходят через каждую точку отдельные частицы.

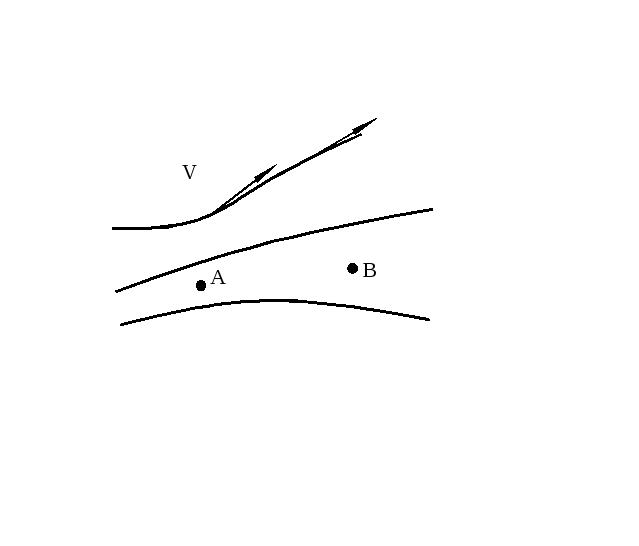
Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в каждой точке пространства.

Условимся проводить линии тока так, чтобы густота их была пропорциональна

Рис.1

величине скорости в данном месте. Тогда по картине линий тока можно будет судить не только о направлении, но и о величине вектора скорости в разных точках пространства (рис.1). Например, в точке А густота линий, а следовательно и модуль, больше, чем в точке В.

Часть жидкости, ограниченная линиями тока, называется трубкой тока.

Течение жидкости называется установившимся (или стационарным), если вектор скорости в каждой точке пространства остается постоянным. При стационарном течении любая частица жидкости проходит данную точку пространства с одной и той же скоростью . Картина линий тока при стационарном течении остается неизменной, и линии тока совпадают с траекториями частиц.

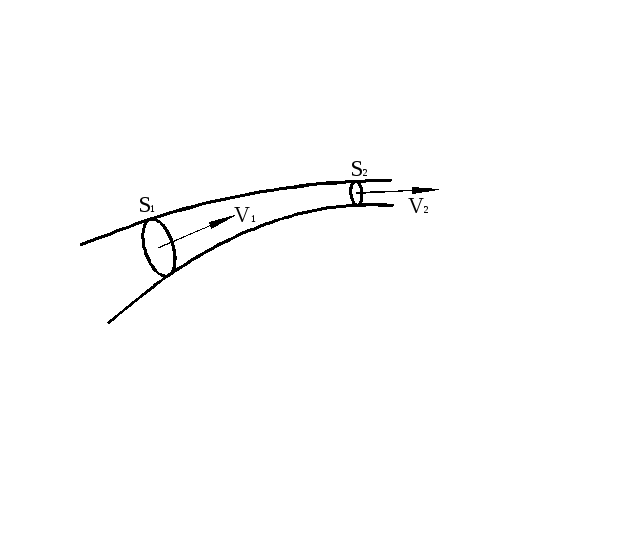
Рассмотрим трубку тока, выберем два ее сечения и, перпендикулярные направлению скорости. Предположим, что во всех точках сечения скорость частиц

Рис.2

жидкости одинакова. За одну секунду через сечение пройдет объем жидкости, а через сечение-(рис.2). Если жидкость несжимаема (то есть плотность ее всюду постоянна), то количество жидкости между сечениямиибудет оставаться неизменным. Отсюда следует, что объемы жидкости, протекающие за единицу времени через сеченияидолжны быть одинаковы

=.

Следовательно для несжимаемой жидкости при стационарном течении величина в любом сечении данной трубки должна быть одинакова

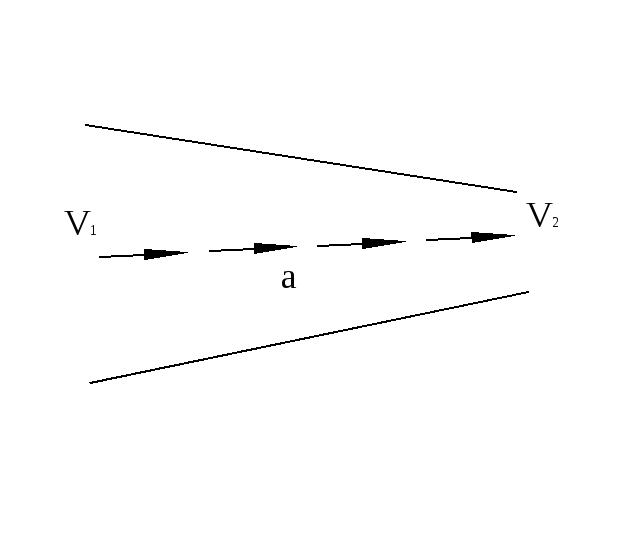
Это выражение есть теорема о неразрывности струи. Из него следует, что при переменном сечении трубки тока частицы несжимаемой жидкости движутся с ускорением (см. рис.3)

	Теорема о неразрывности струи применима к реальным жидкостям и даже к газам в том случае, когда их сжимаемостью можно пренебречь. Расчеты показывают, что при движении жидкостей и газов со скоростями, меньшими скорости звука, их можно считать несжимаемыми.
Рис. 3

2. Уравнение Бернулли.

Изучение движения реальных жидкостей и газов представляет собой сложную задачу. Поэтому для ее упрощения пренебрегают силами внутреннего трения. Воображаемая жидкость, в которой полностью отсутствует внутреннее трение называется идеальной.

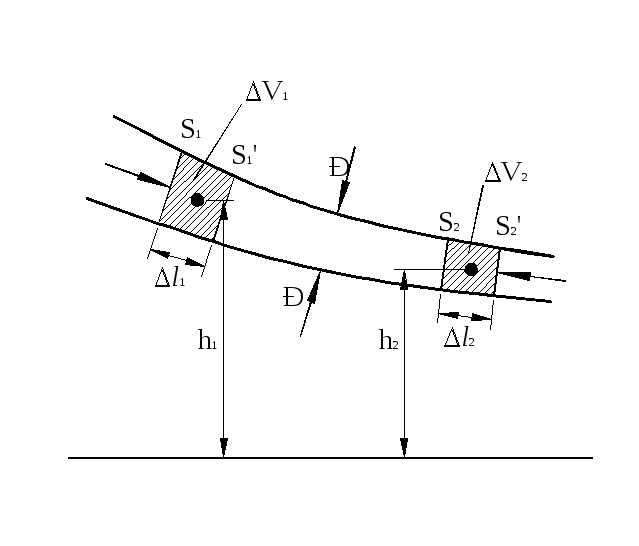
Рассмотрим стационарное течение несжимаемой идеальной жидкости. Выделим объем жидкости, ограниченный стенками узкой трубки тока и перпендикулярными к линиям тока сечениями и(рис.4). За времяэтот объем сместится вдоль трубки тока,

причем граница сместится к, получив перемещение, а границак, получив перемещение. Работа, совершаемая при этом силами давления, равна приращению полной энергии в рассматриваемом объеме жидкости. Силы давления на стенки трубки тока перпендикулярны в каждой точке к направлению перемещения жидкости, и

поэтому работы не совершают. Отлична от нуля только работа сил давления, приложенная к сечениям и. Эта работа равна

=(1)

Вследствие несжимаемости жидкости за время через сеченияипройдет один и тот же объем жидкости, то есть. Тогда выражение (1) примет вид

(2)

Полная энергия рассматриваемого объема жидкости складывается из кинетической энергии и потенциальной энергии в поле сил земного тяготения. Вследствие стационарности течения полная энергия жидкости между сечениями иза времяизменится за счет работы. Поэтому приращение полной энергии рассматриваемого объема равно разности значений полной энергии объемови, масса которых,.- плотность жидкости.

Возьмем сечение трубки тока и перемещениенастолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости, давленияи высотыТогда для приращения полной энергии получается выражение

-(3)

Приравнивая выражения (2) и (3), сокращая на и перенося члены с одинаковыми индексами в одну часть равенства, получим

=(4)

Сечения ивыбирались произвольно, поэтому для любого сечения

(5)

Выражение (5) выведено швейцарским физиком Даниилом Бернулли и получило название – уравнение Бернулли.

Несмотря на то, что уравнение выведено для идеальной жидкости, оно применимо для реальных жидкостей, внутреннее трение которых не очень велико.

Величина в формуле (5) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина- динамическим давлением, а величина- гидростатическим давлением. Для горизонтальной трубки тока выражение (5) принимает вид

=, (6)

то есть давление оказывается меньшим в тех точках, где скорость больше.

Уменьшение давления в точках, где скорость больше, положено в основу устройства водоструйного насоса (см. рис. 5)

Струя воды подается в трубку, открывающуюся в атмосферу, так что на выходе из трубки давление равно атмосферному. В трубке имеется сужение, по которому вода идет с большой скоростью, поэтому давление в этом месте оказывается меньше атмосферного. Такое давление устанавливается и в охватывающей трубку камере насоса, которая сообщается с трубкой через разрыв, имеющийся в узкой части трубка. Подсоединив к камере насоса откачиваемый объем, из него можно откачать воздух до давления порядка 100 мм рт. ст. (ртутного столба).

Рис. 5.

Сумма статического и динамического давленияназывается полным давлением

.

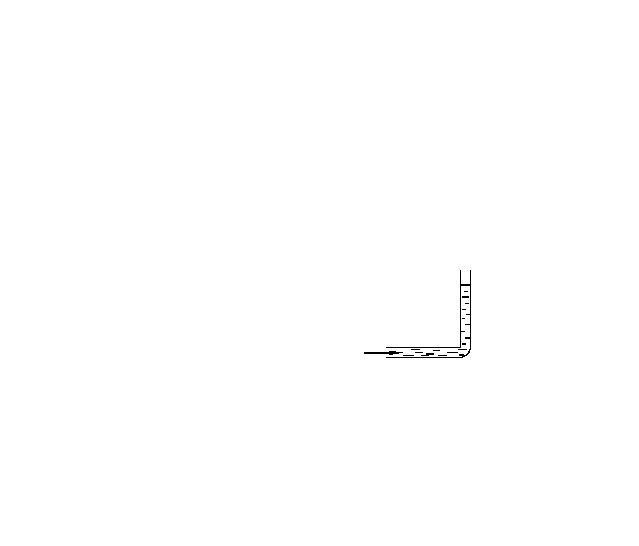
Для измерения полного давления используется трубка Пито. Это небольшая изогнутая манометрическая трубка, обращенная открытым концом навстречу потоку жидкости (см. рис. 6) Линии тока, направленные к трубке Пито, заканчиваются внутри трубки, где жидкость покоится, то есть скорость жидкости изменяется отдо 0. Высота столба жидкости, устанавливающаяся в трубке является поэтому мерой максимального давления, то есть полного напора жидкости.

Рис.6.

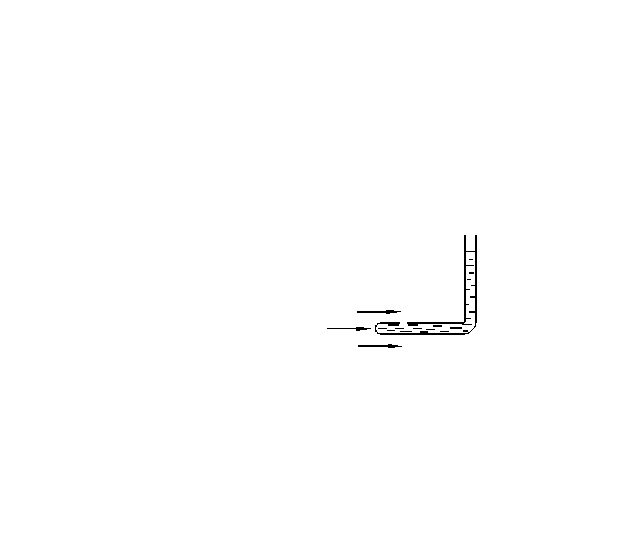
Для измерения статического давления в поток вводят изогнутую трубку с закрытым концом и боковым отверстием (см. рис.7).

	Такая трубка называется зондом. Скорость жидкости вблизи отверстия (а следовательно и давление) будет мало отличаться от скорости (и давления) в невозмущенном потоке. Поэтому манометр, присоединенный к зонду покажет статическое давление .
Рис. 7

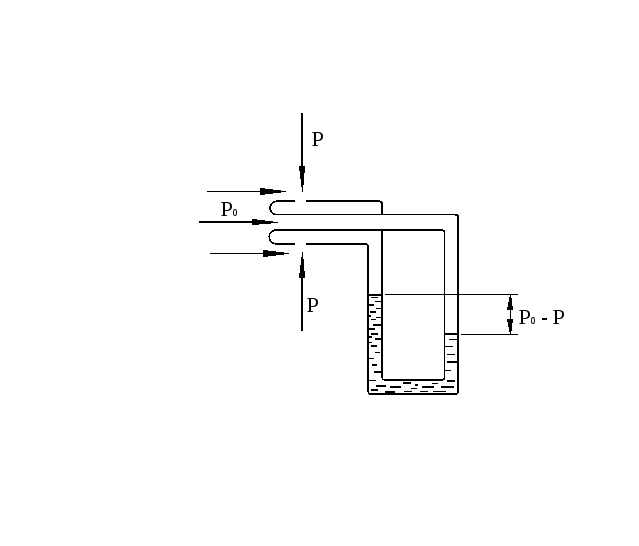
Прандтль трубку Пито соединил с зондом (см. рис. 8) Получившийся прибор измеряет

	разность полного и статистического давления, то есть динамическое давление . Для заданной плотности манометр можно проградуировать в значениях скорости. Поэтому трубка Пито-Прандтля может служить прибором для измерения скорости течения жидкости или газа.
Рис.8.