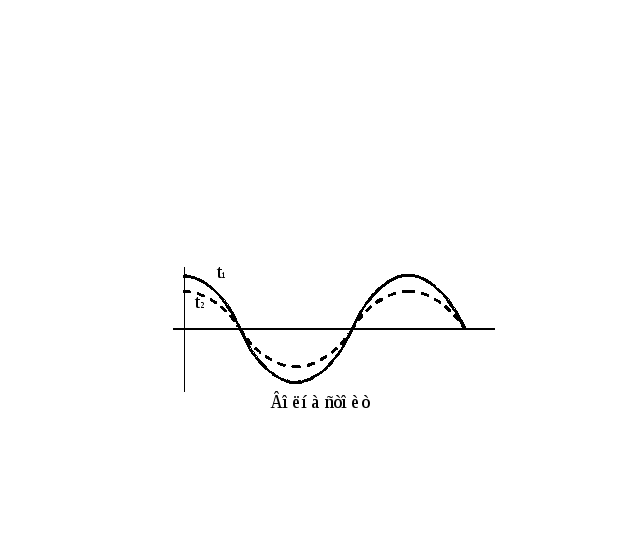
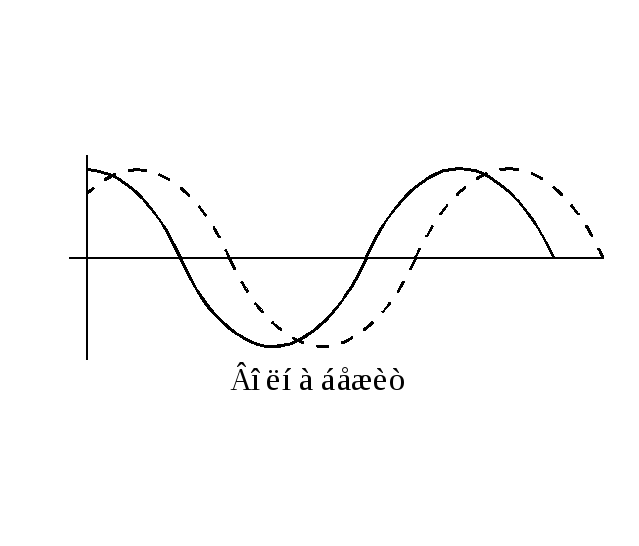
2. Фазовая скорость.

Зафиксируем какое либо значение фазы волны

.

Это выражение дает связь между моментом времени и координатой точки, где фаза имеет выбранное значение.- меняются так как полное выражение постоянно, то есть фиксированное значение фазы с течением времени перемещается. Найдем скорость ее перемещения. За малоеизменится на

- фазовая скорость.

- скорость распространения волны.

.

Скорость, с которой перемещается воображаемая фазовая поверхность, на которой находятся точки, имеющие всегда одинаковую фазу, называется фазовой скоростью.

3. Волновое уравнение.

Дифференциальное уравнение, описывающее волновой процесс называется волновым уравнением. Уравнение волн является решением этого уравнения.

Уравнение плоской волны

.

Дифференцируем его дважды по и по

.

Из последнего следует

.

И поэтому

- волновое уравнение (одномерный случай).

Трехмерный случай волнового уравнения

.

Решением этих уравнений является уравнение волны.

Вывод: Если мы установили, что какой либо процесс описывается волновым уравнением, то мы обязаны сделать вывод, что этот процесс является волновым и что нечто распространяется в пространстве как волна.

4. Стоячие волны.

Стоячая волна получается при сложении( интерференции) прямой и отраженной волны.

- прямая волна,

- отраженная волна.

=

Изобразим стоячую волну в некоторый момент времени

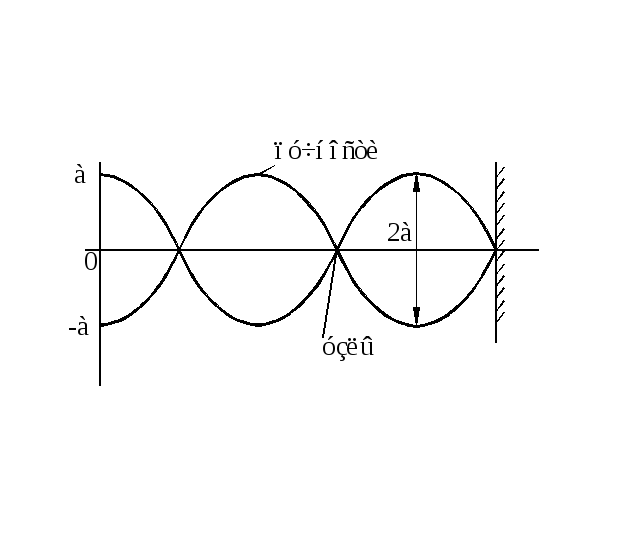
Для стоячей волны характерны узлы и пучности. Найдем их координаты.

1). Узлы, ,

,

Расстояние между узлами

Узлы отстоят друг от друга на

2). Пучности, .

Расстояние между двумя соседними узлами или пучностями называется длиной стоячей волны .

4. Сравним стоячую волну с бегущей.

Амплитуда:

- зависит от, для разных точек величина разная. В узле= 0 в пучностимаксимальна.

б). Фаза стоячей волны Все точки в любой момент имеют одинаковую фазу. Они одновременно в нуле, и одновременно в максимуме (см. рисунок).

Фаза бегущей волны, в одно время фазы разных точек разные (см. рисунок).

в).

г). Стоячая волна не переносит энергию. Бегущая волна переносит энергию.

5. Звуковые волны.

Звуковыми волнами называются волны, распространяющиеся в упругой среде и обладающими частотами от 16 до 20 000 Гц. Они воспринимаются органам и слуха. Звук с частотами Гц называется инфразвуком, волны с частотой20 000 Гц – ультразвуком.

Интенсивностью звука называется среднее значение плотности потока звуковой энергии . Она численно равна энергии, перенесенной за единицу времени через единичную площадку и измеряется в Вт/м². Интенсивность звука пропорциональна А².

Чувствительность человеческого уха к различным частотам различна. Наиболее оно чувствительно к частотам от 700 до 6000 Гц. В этом диапазоне оно воспринимает звук с силой 10^-12-10^-11Вт/м². Наименьшая интенсивность звука, воспринимаемая ухом называется порогом слышимости.

Если интенсивность превышает некоторый предел, то звук не слышен, он вызывает болевые ощущения. Порог болевого ощущения также зависит от частоты. Он примерно равен 1 Вт/м². Интенсивность является объективной характеристикой звука, громкость - субъективной. Если интенсивность растет по геометрической прогрессии, то громкость – по арифметической. Поэтому уровень громкости, определяется как,- пороговая чувствительность, 10^-12 Вт/м² . Уровень громкости измеряется в беллах, децибелл в 10 раз меньше

Скорость распространения звуковой волны в газах изменяется по формуле

- молярная масса. Для воздуха, при Т=273 К,=331 м/с.