6. Механические волны (упругие волны)

Если в каком то месте упругой среды возбудить колебания частиц среды, то вследствии взаимодействия частиц среды это колебание будет распространяться от одной частицы среды к другой со скоростью . Среда охватывается волновым процессом.

Процесс распространения колебаний в пространстве называется волной.

Частицы среды, в которой распространяется волна совершают колебательные движения и не вовлекаются волной в поступательные движения в направлении движения волны. Поэтому волна не переносит массу, за исключением ударных волн.

Волны бывают поперечные и продольные.

Волна называется поперечной, если колебания частиц среды происходят в направлении, перпендикулярном направлению распространения волны. Поперечная волна называется неполяризованной, если колебания частиц происходят в разных плоскостях. Волна поляризована, если колебания происходят в одной плоскости. Поперечные волны могут распространяться только в твердых телах,

,

где - модуль сдвига среды,- плотность среды.

Волна называется продольной, если направление колебательных движений частиц совпадает с направлением распространения волны. Продольные волны могут распространяться в твердых телах, жидкостях и газах. Скорость их

,

где - модуль Юнга,- плотность среды.

О поляризации здесь не говорят.

Область пространства, в которой в которой распространяется волна, называется волновым полем.

Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой

поверхностью. Волновая поверхность, отделяющая волновое поле от остальной части среды называется фронтом волны.

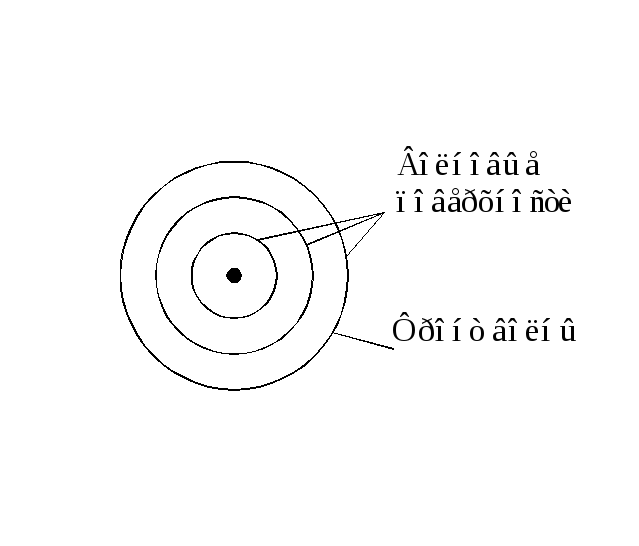
Волновая поверхность, фронт волны могут иметь различную форму. В зависимости от формы фронта волны имеются, например, плоские и сферические волны.

Лекция 9 Уравнение плоской гармонической волны.

1. Фронт волны

Фронт волны – плоскость. Процесс распространения колебаний, то есть волна, описывается гармоническим законом. Пусть волна распространяется в направлении , а- отклонение колеблющейся точки от положения равновесия. Тогда после вовлечения точки=0 в колебания

.

Эта точка, колеблясь, тянет за собой соседние точки, те следующие, и в итоге происходит распространение волны. Но чем дальше от начала лежит точка А, вовлекаемая в колебательный процесс, тем позже она начнет колебаться.

- время запаздывания, по прошествии которого точка А вовлекается в колебательный процесс. Смещение точки А:

,

- скорость распространения волны.

- уравнение плоской гармонической волны.

,

,

- длина волны, расстояние, пройденное волной за период.

- уравнение плоской гармонической волны.

- волновое число.

уравнение плоской гармонической волны

Анализ.

1). Фиксируем момент времени

- описывает положение точек волны в пространстве.

2).Фиксируем точку , находящуюся на определенном расстоянии от начала отсчета.

- описывает положение точки волны во времени.

3). Найдем разность фаз двух точек, отстоящих от источника колебаний соответственно на ив некоторый момент времени

а) . Точки, находящиеся на расстоянии кратномколеблются в одной фазе. Они одновременно бывают в максимуме, нуле минимуме и т.д.

В этом случае

Минимальное расстояние между точками, колеблющимися в одной фазе есть длина волны этих волновых процессов.

б).

.

Точки, отстоящие друг от друга на нечетное число полуволн, колеблются в противофазе.