6. Момент импульса относительно неподвижной точки.

Моментом импульса материальной точки аотносительно неподвижной точки 0 называется физическая величина, равная векторному произведению

, (20)

где - радиус-вектор проведенный из точки 0 в точку а,- импульс материальной точки.

Рис.9.

Направление вектора совпадает с направлением поступательного движения правого винта при его вращении отк. Модуль вектора момента импульса

(21)

где - угол между векторамии,- плечо вектораотносительно точки 0. Моментом импульса системы материальных точек относительно неподвижной точки 0 называется векторная сумма моментов импульсов всех материальных точек системы относительно той же точки 0

(22)

7. Момент импульса относительно неподвижной осиz.

Моментом импульса материальной точки аотносительно неподвижной осиzназывается скалярная величина, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса не зависит от положения точки 0 на осиz.

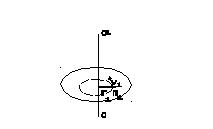
Рис.10.

Рассмотрим вращение твердого тела вокруг неподвижной оси z(О-О¹). Каждая точка твердого тела описывает горизонтальную окружность радиусасо скоростью. Скорость.и импульсперпендикулярны этому радиусу, поэтомурадиус является плечом вектора(угол=90⁰). Момент импульса каждой точки твердого тела относительно осиzравен

(23)

и направлен по оси в сторону, определяемую правилом правого винта. Моменты импульса всех точек твердого тела будут сонаправлены, поэтому момент импульса твердого тела относительно оси есть сумма моментов импульсов отдельных частиц

,

то есть все точки твердого тела вращаются с одинаковой угловой скоростью, то wможно вынести за знак суммы

,

то есть

..

Момент импульса твердого тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость.

Лекция 6. Уравнения динамики вращательного движения.

1. Закон сохранения момента импульса.

Продифференцируем момент импульса по времени

.

Величина есть скорость материальной точки, связанная с ее импульсом соотношением. Поэтому первое слагаемоеравно нулю как векторное произведение коллинеарных векторови, () Второе слагаемое можно преобразовать с помощью уравнения Ньютона

.

Тогда

. (1)

Это уравнение моментов относительно неподвижной точки. Производная по времени момента импульса материальной точки (относительно неподвижной точки) равна моменту силы относительно этой же точки.

Уравнение моментов (1) можно обобщить на случай произвольной системы материальных точек. Пусть система состоит из nматериальных точек вращающихся вокруг центра 0.

+

+

…………………….

+

где - момент внутренних сил,- момент внешних сил.

По третьему закону Ньютона = 0, так как внутренние силы входят попарно, сила с которой одно тело действует на другое равно и противоположно направлена сила с которой второе тело действует на первое. Полный момент этих сил равен нулю (см. рис.)

,

Исходя из этого уравнение примет вид

,

где - момент импульса системы материальных точек.

=- момент всех сил действующих на систему материальных точек.

(2)

Основной закон динамики вращательного движения для системы материальных точек. Производная по времени от момента импульса системы материальных точек относительно неподвижной точки равна геометрической сумме моментов всех внешних сил относительно этой точки.

Если момент всех внешних сил относительно неподвижной точки равен нулю, то момент импульса системы относительно той же неподвижной точки остается постоянным во времени.

иили(3)

Выражение (3) – математическая запись закона сохранения момента импульса. Если мы продифференцируем по времени момент импульса относительно неподвижной оси, то получим уравнение моментов относительно неподвижной оси

(4)

Как было показано ранее, момент импульса твердого тела относительно оси вращения равен

.

Если момент инерции при вращении остается постоянным, то

,

где- угловое ускорение. Тогда

(5).

Произведение момента инерции твердого тела относительно оси вращения на угловое ускорение равно моменту внешних сил относительно той же оси.

Уравнение (5) – основное уравнение динамики вращательного движения вокруг неподвижной оси. Оно напоминает уравнение Ньютона для поступательного движения.

Роль массы mиграет момент инерцииJ, роль скоростиv– угловая скоростьw, роль с илыF– момент силыM, роль импульсаp– момент импульсаL. Момент импульсаLчасто называют вращательным импульсом системы.

Если момент внешних сил M_zотносительно оси вращения равен нулю, то вращательный импульс сохраняется:

(6)

Продемонстрировать закон сохранения импульса можно с помощью скамьи Жуковского. Скамья Жуковского представляет собой стул, сиденье которого имеет форму диска. Диск может свободно вращаться вокруг вертикальной оси на шариковых подшипниках.

Человек, оттолкнувшись ногой от пола, приводит скамью во вращение. Вместе со скамьей будет вращаться и он сам. Во время вращения момент импульса системы скамья плюс человек будет оставаться постоянным, какие бы внутренние движения не совершались в системе.

Если человек разведет руки в стороны, то он увеличит момент инерции системы J, а потому угловая скорость вращенияwдолжна уменьшиться, чтобы оставался неизменным вращательный импульсL=Jw(см рис 1а и 1б)

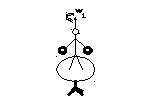
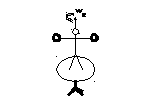
Рис.1а. L=J₁w₁Рис.1бL=J₂w₂

J₁w₁=J₂w₂(J₂>J_1,w₂<w₁)

Если человек, стоя на неподвижной скамье Жуковского, начинает делать конические движения над головой, скамья начинает вращаться в другую сторону (рис.2).

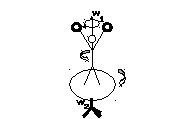
Общий момент импульса системы остается равным нулю.

Когда винт судна начинает вращаться, по закону сохранения момента импульса системы, корпус судна должен вращаться в противоположную сторону. В обычных условиях это не страшно, но в критических ситуациях (сильная боковая волна, легкое судно) может привести к опрокидыванию судна. Эта же ситуация всегда реализуется и для вертолетов. Чтобы этого не происходило, на хвосте устанавливается другой винт для гашения вращения.

В заключении сопоставим основные величины и уравнения определяющие вращение тела им его поступательное движение.

Поступательное движение	Вращательное движение
Масса m Скорость v = dr/dt Ускорение a = dv/dt Сила F Импульс p = mv Основное уравнение динамики F = ma F = dp/dt Работа dA = F ds Кинетическая энергия mv2/2	Момент инерции J Угловая скорость w = dφ/dt Угловое ускорение ε = dw/dt Момент силы M = Fr Момент импульса L = Jw Основное уравнение динамики M = Jε M = dL/dt Работа вращения dA = Mdφ Кинетическая энергия вращения Jw2/2