26. Системы с запаздыванием

Системами с запаздыванием называются системы, структурные схемы которых содержат хотя бы одно звено запаздывания. Это звено характеризуется зависимостью между входной величиной U(t) и выходом x(t) вида

x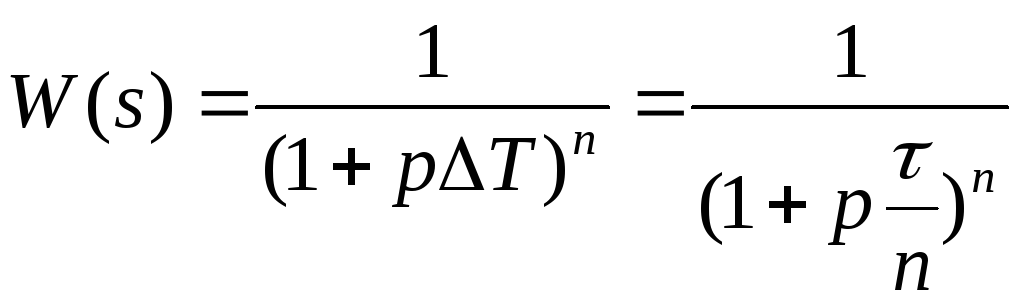(t)=U(t-), где: τ является постоянной величиной— время запаздывания. Система с запаздыванием может рассматриваться как система, состоящая из последовательного соединения большого числа инерционных звеньев с малыми постоянными времени. Пусть система состоит из n последовательно включ равных инерционных звеньев с постоянным временем ΔT заменим его на /n. Тогда перед функция разомкнутой системы при коэфф. усиления =1 имеет вид:

Тогда при n ∞ в пределе получим величину W(s)=exp(-sτ) т.е. функция звена с запаздыванием.

Звено с запаздыванием является одним из простейших типов систем с распределенными параметрами.

27. Нелинейные системы, общие понятия, особенности динамики, типовые нелинейности.

Нелинейная САУ – имеет хотя бы одно звено системы описывается нелинейным уравнением. Различают статические и динамические нелинейности. Статические нелинейности представляются в виде статических нелинейных характеристик. Динамические характеристики в виде нелинейных дифференциальных характеристик.

-В нелинейной системе выходная реакция может стремиться к бесконечности на конечном интервале времени

-выходной сигнал при отсутствии входного сигнала не обязательно стремится к нулю.

-возможны устойчивые колебания определенной амплитуды и частоты независимо от начальных условий

- при синусоидальном входном сигнале на выходе могут присутствовать дополнительные гармоники, поэтому частота выходного сигнала кратна частоте входного.

-может наблюдаться скачкообразный резонанс частоты выходного сигнала.

Основные виды нелинейностей

Звено с зоной нечувствительности: при малых изменениях значений входа, выход не меняется.

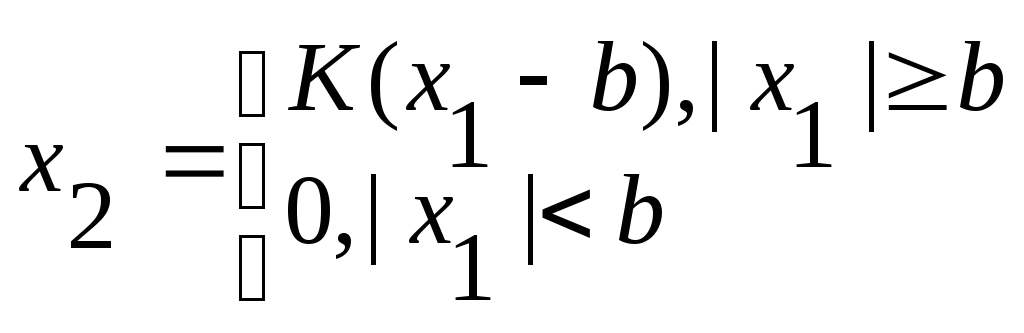
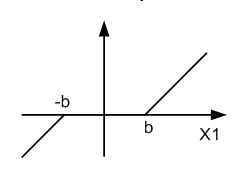
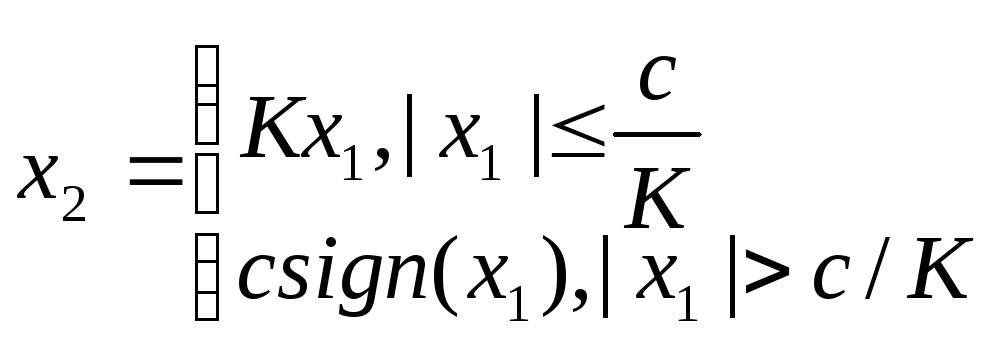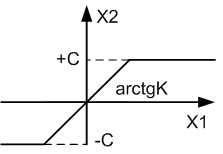
Звено с ограничением: при малых значениях входа линейно, при больших нет:->

<-Релейная характеристика

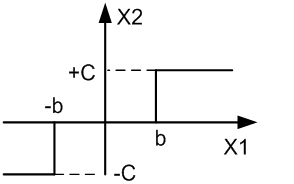
3-х позиционное реле, или реле с зоной нечувствительности:->

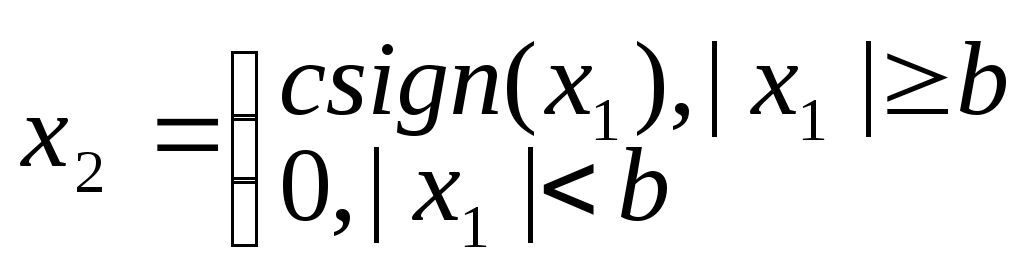
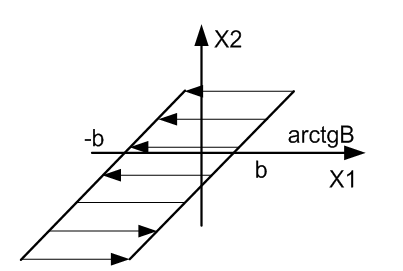
<-Характеристика сухого трения звено типа люфт

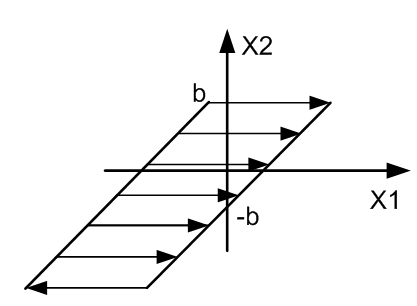
Нелинейность типа упор Регулирование противоположно с люфтом:->

28. Метод малых отклонений. Первый метод Ляпунова. Типы особых точек

Составляя уравнения для малых отклонений от состояния равновесия либо установившегося движения, можно исследовать устойчивость данного состояния равновесия (движения). Исследование обычно ведется с помощью устойчивости по Ляпунову и 1-му методу Ляпунову.

Дифференциальное уравнение замкнутой системы 2-го порядка можно преобразовать в систему из 2-ух уравнений 1-го порядка:

Это уравнение фазовой траектории интегральной прямой на фазовой плоскости. Вблизи начала координат фазовая траектория (1) раскручивается и стремится к предельному циклу. Фазовая траектория (2) начинается вне предельного цикла, может со временем к нему сходиться, следовательно, система описываемая (1) – неустойчива относительно положения равновесия, но при этом всякое равновесие со временем переходит в предельный цикл. Если амплитуда предельного цикла мала, то такое поведение системы при больших сигналах приемлемо, т.е. система неустойчива при малых отклонениях от положения равновесия, и устойчива при значительных отклонениях.

Ляпунов: если 1-ое приближение системы устойчиво, то и нелинейная система – устойчива.

Типы особых точек: точки равновесия – из них могут исходить многие траектории

Центр	Устойчивый фокус	Неустойчивый фокус	Устойчивый узел	Неустойчивый узел	Седло
Re(λ1)=Re(λ2)=0, Im(λ)!=0	Re(λ)<0 Im(λ)!=0	Re(λ)>0 Im(λ)!=0	Re(λ)<0 Im(λ)=0	Re(λ)>0 Im(λ) =0	Re(λ1)>0 Re(λ2)<0, Im(λ) =0

Седло всегда неустойчиво.