32. Методы малого параметра (аналитические методы)

Методы малого параметра дают возможность приближенно исследовать устойчивость нелинейных систем, определять амплитуды и частоты автоколебаний в системах, а также устойчивость этих автоколебаний (предельных циклов). Наиболее ранними являются методы Пуанкарэ, Ляпунова. Рэйли и Ван-дер-Поля. Л.И. Мандельштамом, Н.Д. Папалекси и А.А. Андроновым был строго обоснован и метод Ван-дер-Поля, развит метод Пуанкарэ. Б.В. Булгаковым эти методы были распространены на системы высокого порядка. Н.М. Крылов и Н.Н. Боголюбов Разработали принцип так называемого гармонического баланса. Широкое пременим метод Л.С. Гольдфарба, базирующийся на использовании принципа гармонического баланса, хотя он уже относится к графоаналитическим методам.

В первой фазе развития методов малого параметра рассматривались нелинейные системы второго порядка. Например, уравнение лампового генератора может быть приведено к виду (для относительного времени):

Здесь φ – нелинейная функция x и , μ – некоторое постоянное число, считающееся малый по величине. Это и есть малый параметр. Если μ=0, то уравнение (1) вырождается в простое линейное уравнение

Имеющее очевидное значение , где амплитуда А зависит от начальных условий, а частота ω=1. Между тем при μ≠0, как следует, например, из эксперимента, получается автоколебание вида

, где А – определенная амплитуда, независимая от начальных условий, а частота ω близка к единице, но несколько от неё отличается.Автоколебание, как следует из формулы (4), примерно синусоидально, если μ не велико.Уравнение (1) при μ=0 имеет известное решение х0 (3). При малом μ, не равном нулю, естественно представить это решение в форме, близкой к х0,а именно , где х1, х2 и т.д. – некоторые функции времени. Если эти функции найдены, то ограничившись некоторым числом членов рядя (5), получаем приближенное решение, обращающееся в частном случае μ=0 в функцию х0(t) – решением уравнения линейной консервативной системы (2). Методы малого параметра имеют принципиальное ограничение – они и качественно и количественно предают хорошо черты явления лишь в том случае, когда система в известном смысле мало отличается от консервативной, имеющей решение, соответствующее μ=0. Если система сильно отличается от исходной, то методы малого параметра уже не описывают достаточно точно происходящие явления и могут даже дать качественно неверный результат.

33. Метод гармонического баланса.

М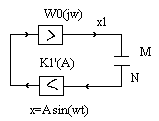етод исследования устойчивости систем содержащих 1 нелинейное усилит звено с коэффициентом усиления К1’(A) и любую линейную часть с комплексным коэффициентом передачи W0(jw). Пусть систем находится на границе устойчивости и в ней возникают незатухающие колебания частоты w x – вход нелинейного звена,- пусть колеблется с амплитудой А. Разомкнем систему между точками М и N и подадим на вход синус колебание х той же амплитуды и частоты. Тогда выходное колебание Х₁ будет = по амплитуде и обратно по фазе входному (т.к. система на границе устойчивости) => условие возникновения автоколебаний принимает вид: W(jw)=W0(jw)K1’(A)=-1 или преобразив – W0(jw)=1/ K1’(A) приравнивая, мнимую и действительную части 0 получаем 2 уравнения с неизвестной частотой и амплитудой автоколебаний. Решаем их, если в результате получим положение действительного значения, то автоколебаний возможны. Можно решать графически. Строя W0(jw) и -1/ K1’(A) точки пересечения определяют частоту и амплитуду автоколебаний. Если не пересекает, то нет автоколебаний, если касаются, то система находится на границе устойчивости. Уменьшая величину W0(jw) можно избежать пересечения, и сделать систему устойчивой. Пересечение кривых указ лишь на возможность существование в системе автоколебаний, предельный цикл реализуем в системе лишь, когда он устойчив.