ОТВЕТЫ

1.Классификация измерений. Измерения прямые, косвенные, совместные и совокупные.

Измерения классифицируют по разным признакам:

1.По характеру зависимости измеряемой величины от времени:

статические и динамические.

2.По виду измеряемой величины: аналоговые и дискретные.

3.По числу измерений: однократные и с многократными наблюдениями

(результат измерений получается при статистическом усреднении результатов отдельных наблюдений).

4.По условиям измерений: равноточные и неравноточные.

5.По метрологическому назначению: технические (не связаны с передачей размера единицы ФВ) и метрологические (связаны с передачей размера единицы ФВ).

6.По степени точности: прецизионные, высокоточные, лабораторные, точные, технические.

7.По выражению результата измерений: абсолютные (результат выражен в единицах ФВ) и относительные (результат выражен в децибелах).

8.По связи с объектом: бесконтактные и контактные.

9.Наиболее распространена классификация по общим приёмам получения результата: прямые, косвенные, совокупные и совместные.

Прямое измерение — искомое значение ФВ получают непосредственно из опытных данных. Например, измерение напряжения вольтметром.

Косвенное измерение — значение ФВ получается на основании результатов прямых измерений других ФВ, связанных с искомой ФВ известной функциональной зависимостью.

Совместные измерения — проводимые одновременно измерения нескольких неодноимённых величин с целью определения зависимости между ними.

Совокупные измерения — проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения ФВ определяются путём решения системы уравнений, получаемых при прямых измерениях различных сочетаний этой величины

2.Классификация методов измерений ФВ. Метод непосредственной оценки и метод сравнения с мерой.

Физическая величина (ФВ) — характеристика одного из свойств физического объекта, общая в качественном отношении многим физическим объектам, но в количественном отношении индивидуальная для каждого объекта.

Методом измерения называется совокупность приёмов сравнения измеряемой ФВ с её единицей. Классификацию методов можно проводить по разным признакам.

1.По физическому принципу, положенному в основу измерения,

различают методы измерения электрические, магнитные, акустические, оптические, механические и т.д.

2.В зависимости от режима взаимодействия СИ и объекта измерения методы делят на статические и динамические.

3.По виду измерительных сигналов можно выделить аналоговые и цифровые методы измерений.

4.Наиболее распространенная классификация — по совокупности приёмов использования принципа и средств измерений. Отличительным признаком такой классификации является способ использования меры в измерительном эксперименте. Различают метод непосредственной оценки и метод сравнения с мерой.

Метод непосредственной оценки — значение ФВ определяют непосредственно по отсчётному устройству измерительного прибора, шкала которого была заранее проградуирована с помощью многозначной меры.

Метод сравнения с мерой — измеряемую величину сравнивают с образцовой величиной, воспроизводимой мерой. Теоретически метод более точен, чем метод непосредственной оценки.

Нулевой – действие измеряемой величины на прибор сравнения полностью уравновешивается образцовой, т.е. выходные показания прибора сравнения доводят до нуля.;

Дифференциальный – на прибор воздействует разность измеряемой ФВ

иобразцовой ФВ. Неизвестная величина определяется по известной образцовой величине и измеренной разности. (взвешивание на циферблатных весах с использованием гирь);

Замещения – измеряемую величину последовательно во времени замещают на образцовую, изменяя ее до того же показания прибора, которое было при измерении неизвестной ФВ;

Совпадения – измеряемую величину определяют по совпадению отметок шкал или периодических сигналов. (штангенциркуль);

Противопоставления – измеряемая величина и мера одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами. (взвешивание на равноплечих весах); Дополнения – значение измеряемой величины дополняется образцовой величиной с таким расчетом, чтобы на прибор воздействовала их сумма, равная заранее заданному значению. Отсчет производится по известной ФВ.

Нулевой метод и метод замещения являются высокоточными.

3. Классификация средств измерений. Их характеристики.

Средством измерения называется техническое средство, предназначенное для измерений.

В связи с широким многообразием СИ их классификацию проводят по разным признакам:

1.По роли, выполняемой в системе обеспечения единства измерений, СИ делятся на метрологические (предназначены для передачи размера единиц ФВ рабочим СИ) и рабочие (применяются для измерений, не связанных с передачей размера единицы ФВ).

2.По уровню автоматизации СИ делятся на неавтоматические; автоматизированные (производят автоматически только часть измерительных операций); автоматические (производят автоматически все измерительные операции).

3.По уровню стандартизации СИ подразделяются на стандартизованные (соответствующие какому-либо стандарту) и нестандартные.

4.По отношению к измеряемой ФВ СИ подразделяются на основные (для измерения именно искомой величины) и вспомогательные (для измерения величины, влияющей на основное СИ или объект измерения).

5.Наиболее распространено подразделение по функциональному назначению.

Элементарные СИ — предназначены для реализации отдельных операций прямого измерения. К элементарным СИ относятся:

Мера — СИ, предназначенное для воспроизведения ФВ заданного размера.

Устройство сравнения (компаратор) — СИ для сравнения двух

однородных величин.

Измерительный преобразователь — СИ, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и хранения, но не поддающейся непосредственному восприятию наблюдателем (т.е. работающие с электрическими сигналами). Примеры: все стандартные электронные блоки

— усилители, счётчики, делители и пр.

Комплексные СИ предназначены для реализации всей процедуры измерения (состоят из элементарных СИ). К ним относятся:

Измерительные приборы — СИ, предназначенные для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем.

Измерительная установка — совокупность функционально объединённых СИ и вспомогательных устройств.

Информационно-измерительные системы — совокупность функционально объединенных измерительных, вычислительных и вспомогательных средств для получения измерительной информации.

Все характеристики (показатели) СИ можно разделить на две группы:

метрологические и неметрологические.

Совокупность характеристик СИ, которая оказывает непосредственное влияние на результаты и погрешности измерений называется

метрологическими характеристиками СИ. Все метрологические характеристики СИ нормируются, т.е. в технической документации на СИ указываются их номинальные значения и допускаемые отклонения от них.

Для каждого вида СИ нормируется свой комплекс характеристик. Чаще всего в документации приводятся следующие основные показатели:

1. Функция преобразования y F(x) — функциональная зависимость между информативными параметрами входного x и выходного y сигналов. 2. Чувствительность СИ по измеряемому параметру. Различают

абсолютную чувствительность S y при x 0 и

x

относительную чувствительность S y .

x / x

3.Постоянная прибора — C 1/ S .

4.Порог чувствительности (реагирования) — наименьшее изменение

входной ФВ.

5.Предельная чувствительность (по напряжению, току, мощности) —

минимальная величина исследуемого сигнала, обеспечивающая нормальную работоспособность прибора.

6.Диапазон измерений — область значений измеряемой ФВ, для которой нормированы допускаемые погрешности СИ.

7.Область рабочих частот (диапазон частот) — полоса частот, в

пределах которой погрешность прибора из-за изменения частоты сигнала не превышает допускаемого предела.

8.Цена деления шкалы — разность значений измеряемой величины,

соответствующих двум соседним отметкам шкалы.

9.Разрешающая способность — минимальная разность двух значений ФВ, которая может быть различима.

10.Входное полное сопротивление Zâõ .

11.Выходное сопротивление Zâû õ .

12.Вариация показаний — средняя разность между показаниями прибора.

13.Быстродействие (скорость измерений) — максимальное число измерений в единицу времени.

субъективную (личностную) погрешность — вызывается ошибками оператора при отсчете показаний СИ, отсутствует в цифровых приборах.

3) В зависимости от поведения измеряемой величины во времени

(режим работы СИ) различают погрешности:

статические — погрешности измерения, когда измеряемая ФВ не изменяется за время измерения; динамические — погрешности СИ, когда измеряемая ФВ изменяется во

времени.

4) По условиям эксплуатации СИ различают:

основную погрешность СИ — имеет место при нормальных условиях эксплуатации. дополнительную погрешность СИ — возникает вследствие выхода какой-либо из влияющих величин (температуры и т.п.) за пределы нормальной области значений. Погрешность СИ в реальных условиях называется эксплуатационной или рабочей и представляет собой сумму основной и дополнительной погрешностей.

5) По характеру зависимости от измеряемой величины различают:

аддитивную погрешность — не зависит от измеряемой величины , т.е. погрешность постоянна;

мультипликативную погрешность — зависит от измеряемой величины (линейно или нелинейно).

6) По характеру проявления погрешности делятся:

на систематические погрешности — погрешности, которые остаются неизменными или закономерно изменяются при повторных измерениях одной и той же величины в одних и тех же условиях.

случайные погрешности — при повторных измерениях одной и той же величины изменяются по значению и знаку случайным образом.

грубые погрешности (промахи) — погрешность, величина которой существенно превосходит величину погрешности, обусловленной условиями эксперимента.

Следует различать понятия «погрешность результата измерения» и «погрешность средства измерения». Погрешность результата измерения — это разность между результатом измерения и истинным значением измеряемой ФВ. Она указывает границы погрешности измеренного значения величины. Может включать в себя множество составляющих погрешности, в том числе и погрешности СИ.

Погрешность средства измерения — это разность между показанием СИ и истинным (действительным) значением измеряемой ФВ. Она характеризует точность результатов измерений, проводимых данным конкретным СИ.

5. Систематические погрешности. Обнаружение. Исключение. Систематические погрешности — погрешности, которые остаются неизменными или закономерно изменяются при повторных измерениях одной и той же величины в одних и тех же условиях.

1) По характеру изменения во времени различают:

постоянные систематические погрешности — остаются неизменными (сохраняют величину и знак) в течение всей серии измерений.

переменные систематические погрешности — изменяются в процессе многократных наблюдений.

В свою очередь, переменные погрешности подразделяются:

на монотонно изменяющиеся — в процессе измерения монотонно возрастают или убывают

периодические — погрешности, значения которых являются периодической функцией времени.

прогрессирующие (дрейфовые) — непредсказуемые погрешности.

2) По источнику систематических погрешностей (все три компонента измерений: метод измерений, средства измерений и сам экспериментатор)

несовершенства метода измерений, неточности зависимостей, формул и т.д.

Инструментальные систематические погрешности определяются несовершенством, неидеальностью СИ

Личностные (субъективные) систематические погрешности или погрешности отсчета показаний определяются личностными качествами оператора

Систематические погрешности, обусловленные отклонением внешних условий измерения от нормальных, приведенных в паспорте СИ, называются дополнительными погрешностями и обычно указываются в технической документации СИ.

Обнаружение (выявление) систематических погрешностей и оценку методических систематических погрешностей производят путем теоретического анализа метода измерения с целью определения допущений, упрощений в зависимостях, положенных в основу модели объекта измерений и метода измерений.

Систематические погрешности, обусловленные внешними условиями измерения, выявляются анализом реальных условий измерения для того,

чтобы установить перечень и закономерности проявления влияющих величин.

Для выявления инструментальной систематической погрешности

наиболее простой и надежный, а зачастую и единственно возможный способ

— это поверка используемого СИ. Поверка СИ — совокупность операций, выполняемых в целях подтверждения соответствия СИ метрологическим требованиям.

Систематические погрешности также могут быть обнаружены сравнением результатов измерений, произведенных различными независимыми методами. Переменные погрешности могут быть обнаружены путем статистической обработки нескольких групп наблюдений, снятых при разных условиях измерения.

Постоянные систематические погрешности можно обнаружить путем измерения нескольких величин, связанных известной зависимостью.

Можно выделить следующие методы устранения систематической погрешности:

устранение источников погрешности до начала измерения

(профилактика погрешности)

внесение поправок в результат измерения. Полученный в процессе измерения и содержащий систематическую погрешность результат

называется неисправленным результатом *èçì . Если же систематическая погрешность из результата исключена, то он называется исправленным результатом èçì . Когда погрешность носит аддитивный характер, производится алгебраическое суммирование неисправленного результата и поправки Ï .

исключение погрешности в процессе измерения (коррекция погрешностей).

Используют различные методы коррекции систематических погрешностей. Наиболее часто используются следующие методы:

– метод замещения — заключается в том, что измеряемая величина последовательно во времени заменяется образцовой величиной 0 , получаемой с помощью регулируемой меры, так чтобы показание прибора сохранилось неизменным. Значение измеряемой величины считывается с индикатора меры. При этом систематическая погрешность самого прибора исключается, а погрешность измерения определяется погрешностью меры и погрешностью отсчета измеряемой величины по индикаторам прибора и меры;

– метод компенсации погрешности по знаку позволяет устранить постоянную систематическую погрешность. Измерения проводятся дважды таким образом, чтобы погрешность входила в результаты с разными знаками.

– метод рандомизации основан на переводе систематической погрешности в случайную. Производятся многократные измерения искомой величины (разными однотипными приборами, при разных методиках и условиях измерения и т.д.) и выполняется статистическая обработка полученных результатов. За результат измерения принимается математическое ожидание (среднее арифметическое) всех отдельных измерений, что существенно уменьшает погрешность измерения;

метод противопоставления применяется для устранения постоянных мультипликативных систематических погрешностей. Представляет собой метод сравнения примерно равных измеряемой величины и образцовой

0 .

6.Случайные погрешности. Законы распределения, точечные оценки.

Случайные погрешности — при повторных измерениях одной и той же величины изменяются по значению и знаку случайным образом. Случайные погрешности вызываются большой совокупностью причин, учесть которые невозможно. Случайные погрешности неизбежны и неустранимы.

Хизм = Хист+ΔХобщ; Хобщ = Хсист+ Хслуч. Их анализ производится с помощью аппарата теории вероятности и математической статистики. Основными числовыми характеристиками законов распределения погрешности Х, является математическое ожидание:

[ ]=∫ ( ) ∞−∞. Мат.ожидание – это центр тяжести кривой. Мат ожидание погрешности измерений, есть неслучайная величина, она характеризует систематическую составляющую погрешности измерения, т.е. M[X]=ΔXсист.

Дисперсия показывает степень разброса отдельных значений погрешности относительно M[X] и может служить характеристикой точности проведенных измерений, но имеет размерность в единицах измеряемой величины в квадрате: [ ]=∫( − )2 ( ) ∞−∞. Поэтому в качестве числовой характеристики случайной погрешности чаще используют среднее квадратическое отклонение: =√ . Положительное значение σ называется средним квадратическим отклонением (СКО) случайной величины X, а применительно к погрешностям измерений – средней квадратической погрешностью (СКП) результата измерений.

Коэффиц.корреляции – Rij характеризует степень тесноты линейной завис. двумя случ. велич. Хi и Xj.

Эксцесс – характ. островерш. распред. Е = м4/ 4-3.

Виды распределений реальных погрешностей многочисленны и достаточно разнообразны. Широко известны равномерный (равновероятный), трапецеидальный, треугольный (Симпсона), арксинусоидальный, экспоненциальные и другие законы распределения.

Нормальный закон распределения (распределение Гаусса) нашёл наибольшее применение в метрологии в силу центральной предельной теоремы, утверждающей, что распределение суммы случайных величин, каждая из которых распределена по своему закону, стремится к нормальному распределению.

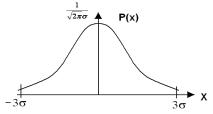
Рис. 2.10 — Нормальное распределение

Значения 3 часто принимают за границы нормального распределения. Рассмотренные функции распределения p(x) являются чисто

теоретическими, и они описывают поведение непрерывной случайной величины. На практике для нахождения числовых характеристик случайной погрешности используются многократные (статистические) измерения, число которых всегда ограничено n . Поэтому как результаты наблюдений, так и их случайные погрешности допустимо считать величинами дискретными. И, следовательно, мы можем найти только оценку, а не сами точные значения каких-то характеристик распределения. Оценка сама является случайной величиной и определяется числом n .

На практике используются различные оценки, характеризующие величину случайной погрешности:

Максимальная погрешность — представляет собой предельную величину случайной погрешности и зависит от закона распределения.

Средняя квадратическая погрешность (СКП) [ X ] и её оценка Sx ,

полученная путем обработки экспериментальных данных, является показателем точности измерений при учете случайных погрешностей.

Квантильная, или интервальная, оценка (доверительный интервал)